Fine chemical processes are integral to modern industries such as automotive, environmental protection, aviation, and new energy. However, these processes involve highly toxic substances and complex chemical interactions, making them vulnerable to uncontrollable circumstances and posing significant risks to human safety and the environment. This work proposes an enhanced GA-LVW algorithm for reliability assessment of fine chemical processes, focusing on essential operating units. The method utilizes global-local structure analysis to extract features from operating unit variables, reducing data noise, simplifying the construction of fuzzy rules, and improving model resilience. The extracted features are integrated into a fuzzy inference system. The proposed approach is validated using the Tennessee Eastman (TE) process model and the R-22 production process in a fluoride facility. Results demonstrate that the enhanced GA-LVW algorithm significantly improves the system’s efficiency and maintainability compared to conventional fuzzy inference systems.
Modern industry places significant importance on fine chemical processes due to their extensive applications across various sectors, including automotive, environmental protection, aviation, new energy, and others [15]. The increasing demand for product variety and the expansion of application domains have heightened the significance of the fine chemical industry. However, the synthesis of fine chemicals often involves highly toxic substances and complex chemical interactions, making the processes highly susceptible to uncontrollable factors, which pose significant risks to human safety and the environment [10,14]. For example, even small leaks of highly toxic compounds used in fluorochemical processes can severely threaten worker safety, equipment functionality, and public property [5]. Traditional monitoring and maintenance methods are struggling to meet the safety and reliability requirements of modern industry, necessitating new strategies for system monitoring and automation [2].
Conventional fine chemical process monitoring systems primarily focus on fault diagnosis and detection. While these systems can minimize losses and promptly repair faults, they are often effective only after the fault has caused irreversible financial losses and safety risks [12]. Recent research highlights that preventing breakdowns alone cannot guarantee system safety and reliability, emphasizing the need for predictive health management (PHM) techniques in the fine chemical sector [8]. These techniques aim to evaluate reliability and implement corrective actions before failures occur.
Reliability evaluation techniques in PHM can generally be categorized into knowledge-based, analysis-based, and data-driven approaches [9]. Knowledge-based approaches rely on expert experience and understanding, but their applicability is limited by production constraints and the unpredictability of expert knowledge. Analysis-based methods leverage physical and chemical principles but struggle to handle the complexity of fine chemical processes, such as time-variation and multivariate coupling [1,16]. On the other hand, data-driven methods overcome these limitations by using extensive process data to build black-box models, offering broader applicability [4].
Although mainstream reliability assessment methods such as reliability block diagrams (RBD), fault tree analysis, Monte Carlo simulations, and Bayesian networks have been widely used in fields like electrical equipment, electronics, aviation, and energy, their application in the chemical industry remains limited [13]. This limitation arises from the multidimensional, strongly coupled, time-lagged, and nonlinear nature of chemical processes, which makes direct application of conventional techniques challenging. Moreover, the reliance on expert knowledge in most existing studies introduces judgmental biases, leading to uncertain reliability evaluation results [11].
To address these challenges, this study introduces a fuzzy inference system (FIS) for the reliability assessment of essential operational units in fine chemical processes, based on global-local structural analysis using an enhanced GA-LVW algorithm. FIS can handle uncertainty and logical reasoning, reducing the dependency on precise expert knowledge. However, its practical application in large-scale chemical processes is often hindered by the excessive number of variables and the complexity of fuzzy rule formulation [3]. By integrating global-local structural analysis, the proposed GA-LVW algorithm extracts features from operating unit variables, replacing the original variables with global-local features as inputs to the FIS. This approach reduces data noise, enhances model resilience, and significantly simplifies the fuzzy rule design, thereby reducing reliance on expert knowledge and expediting the system’s logical design [7].
The methodology is validated using the Tennessee Eastman (TE) process model and the R-22 production process from a domestic fluorination plant. Real-time assessments of the reactor operating unit’s reliability under various operating conditions demonstrate the efficacy of the enhanced GA-LVW algorithm in precise chemical process monitoring. Compared to the conventional FIS approach, the enhanced GA-LVW algorithm not only simplifies fuzzy rule design but also improves system efficiency and maintainability, making it highly applicable in real-world scenarios [6].
The enhanced GA-LVW algorithm proposed in this paper offers a novel approach to predictive health management and reliability evaluation in fine chemical processes. By integrating global and local structural elements, the approach effectively addresses the limitations of existing methods and demonstrates significant potential for broader applications in chemical process monitoring and automation. With advancements in industrial big data, this approach is expected to be further expanded, providing robust support for ensuring the safety and reliability of chemical production.
The Genetic Algorithm (GA) is a heuristic search technique used to find optimal solutions by mimicking natural evolutionary processes. The steps for using GA in feature selection are as follows [11]:
1. **Feature Representation**: Each feature is represented by a binary value, where 1 indicates that the feature is selected, and 0 indicates it is not. A random function generates the initial population. The random function \({f_r}\) in Python’s random module is used in this paper, and it selects elements randomly from the sequence:
\[\label{e1} {f_r} = \text{random choice} (0,1). \tag{1}\]
2. **Fitness Computation**: Compute the fitness value (\({f_i}\)) for each individual \(i\) in the population \(pop(t)\). The fitness value is determined by the fitness function, which evaluates the superiority or inferiority of an individual:
\[\label{e2} {f_i} = \text{fitness}(po{p_i}(t)). \tag{2}\]
3. **Selection**: The selection process involves retaining the fittest individuals from the population to generate the next generation. Using the random competition method, two individuals \(random(po{p_i})\) and \(random(po{p_j})\) are selected, and the one with the higher fitness value is chosen for crossover:
\[\label{e3} \text{winner} = \max \{ \text{random}(po{p_i}), \text{random}(po{p_j}) \}. \tag{3}\]
4. **Crossover**: Two individuals are selected at random, and their genetic material is exchanged to create offspring with better traits. The parent chromosomes before crossover are represented by:
\[\label{e4} \begin{cases} b_1 b_2 b_3 \cdots b_i \mid b_{i+1} b_{i+2} \cdots b_n \\ c_1 c_2 c_3 \cdots c_i \mid c_{i+1} c_{i+2} \cdots c_n \end{cases}. \tag{4}\]
5. **Mutation**: During the search process, mutation alters individual genes to escape local minima and accelerate convergence. A single-point mutation, or bit mutation, changes one bit of the DNA sequence. For instance, 0 is converted to 1, and 1 to 0. The mutation of the fifth bit is shown below:
\[\label{e5} 0111110110. \tag{5}\]
The LVW (Las Vegas Wrapper) algorithm is a feature selection method that uses a stochastic search strategy within the Las Vegas framework and employs the classifier’s error as the evaluation criterion. The following steps outline the LVW algorithm:
1. **Sub-dataset Creation**: Given a dataset \(D\), LVW randomly selects a feature subset \(A'\) to create a sub-dataset \({D^{A'}}\). The dataset is then divided into training and validation sets. Using a designated learning machine \(\xi\), \(k\)-fold cross-validation computes the cross-validation error:
\[\label{e6} {E_i} = \text{CrossValidation} \left( \zeta \left( {D^{A'}} \right) \right), \tag{6}\]
and the average error is calculated as:
\[\label{e7} E_i^\prime = \frac{1}{k} \sum\limits_{i = 1}^k {E_i}. \tag{7}\]
Alternatively, the generalization error \(E'\) on the test dataset can be used as the evaluation criterion:
\[\label{e8} {E^\prime } = \text{Generalization} \left( {\zeta_{\text{train}} \left( {D_{\text{test}}^{A'}} \right)} \right), \tag{8}\] where the feature subset is part of the test sub-dataset.
2. **Updating Global Values**: If the conditions of Eq. (9) are met, update the global minimum error \(E\), the optimal feature subset \(A^*\), the number of feature subsets \(d'\), and the global optimal features \(d\):
\[\label{e9} (E' < E), (E' = E), (d < d'). \tag{9}\]
3. **Termination**: Repeat the above steps until the termination criterion is satisfied.
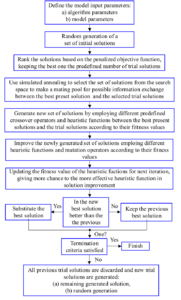
The GA-LVW algorithm combines the global search capability of GA with the feature optimization efficiency of LVW. The algorithm operates as follows:
1. The features of the population are encoded and initialized using GA.
2. LVW randomly selects a feature subset to create a sub-dataset, which is divided into training and validation sets.
3. The fitness of each individual in the population is calculated after selection, crossover, and mutation. Individuals with higher fitness are retained as the current optimal population, and the optimal subset is updated.
4. The algorithm evaluates whether crossover or mutation is needed. If not, the target feature set is output. Otherwise, the process continues until the termination condition of the GA algorithm is satisfied.
Figure 1 illustrates the flow of the GA-LVW algorithm.
The proposed enhanced GA-LVW algorithm was applied to the R-22 manufacturing process dataset of a fluoride plant in China to evaluate its effectiveness. Due to confidentiality agreements, this study introduces the application procedure and results using the reactor operation unit of the R-22 production process as an example.
Dichlorodifluoromethane (R-22) is a commonly used intermediate in fluorochemicals and is widely used as a raw material for propellants and refrigerants. The primary raw materials for R-22 production are hydrofluoric acid and chloroform. The chemical reaction equation is:
\[\text{HCCl}_3 + 2\text{HF} \rightarrow \text{HCF}_2\text{Cl} + 2\text{HCl}.\]
The R-22 production unit includes the reactor, separator, water washing tower, distillation towers, and other equipment. Hydrofluoric acid and chloroform are pumped into the reactor, where they react to produce R-22, R-21, R-23, and HCl. The subsequent process involves fractional distillation, washing, and further distillation to obtain the main product, R-22.
This research utilizes data from January 2023 to October 2023, sampled every minute. The dataset is representative, covering nearly a year and accounting for seasonal changes and feedstock variations. Rigorous safety controls were implemented, and data from shutdowns and maintenance periods were included to simulate abnormal production conditions and validate the method.
To train the GLSA model, 1,000 samples from regular reactor operations were collected. The top three eigenvalues were selected from the 10 reactor operational unit variables, and the remaining samples were projected into three dimensions. These reduced variables served as inputs for the fuzzy inference system. Figure 2 illustrates the fuzzy inference system design.

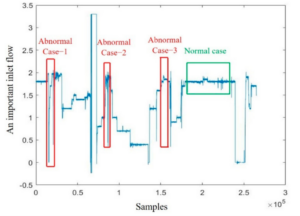
Figure 3 shows the reliability of the reactor operating unit and the critical feedstock input under three abnormal conditions. In Case 1, the critical feedstock initially remains near the target value, and the reactor’s reliability exceeds 90%. However, during a routine maintenance halt, the feedstock drops to zero, and the reliability falls to around 20%. Once the feed is restored, reliability gradually recovers above 90%.
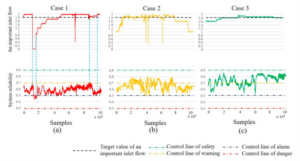
In Case 2, a brief decrease in critical feedstock results in a decline in reactor reliability, approaching the warning limit of 60%. As the feedstock stabilizes, reliability recovers. In Case 3, the feedstock remains stable, and reliability fluctuates between the safety and warning control limits.
A comparison of the enhanced GA-LVW algorithm with expert-guided fuzzy inference systems is shown in Figure 4. While the trends in reliability estimates align, the expert-guided results exhibit larger deviations from the actual system behavior, demonstrating the advantages of the enhanced GA-LVW method.
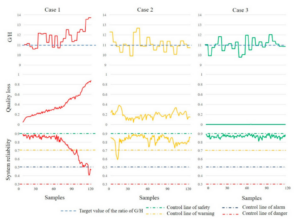
The enhanced GA-LVW algorithm requires only 27 fuzzy rules compared to the 59,045 rules needed for standard FIS, significantly reducing system complexity and enhancing maintainability.
The proposed method was further validated using the Tennessee Eastman (TE) process model. The TE process comprises five operational units: reactor, condenser, separator, stripper, and compressor. The process flow diagram is shown in Figure 5.
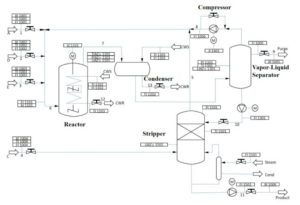
The TE model includes 12 operational variables and 22 process variables. The enhanced GA-LVW algorithm was used to evaluate reactor and separator reliability. The fuzzy inference system required only 27 rules for reactor reliability assessment, compared to 4.30 × 107 rules in the standard FIS approach, highlighting the method’s practicality.
Figure 6 illustrates the affiliation functions of the input and output variables for the TE reactor and separator operational units.
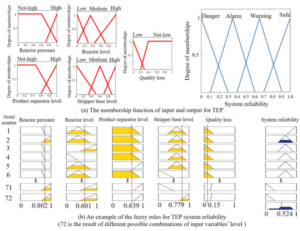
Figure 7 depicts the reliability variation of the TE reactor and separator under three fault scenarios. The enhanced GA-LVW algorithm accurately reflects unit reliability changes, demonstrating its effectiveness in fault detection and system monitoring.
This study proposes an enhanced GA-LVW algorithm for reliability assessment of fine chemical process operating units, combining global-local structure analysis and fuzzy inference systems. The method reduces reliance on expert knowledge, lowers design complexity, and enhances system robustness. Validation using the R-22 process and TE model demonstrates the algorithm’s superiority in improving reliability assessment and maintainability, making it a valuable tool for predictive health management in complex chemical processes.