The combination of thermal power units’ stability and energy storage systems’ rapid response time enhances power system frequency control. However, high costs and battery life impacts from charging/discharging strategies limit energy storage adoption. This study proposes an adaptive weight-based particle swarm optimization algorithm (APSO) to optimize energy storage control for joint thermal-storage frequency modulation (FM). By analyzing the coupling between state of charge (SOC) and charging/discharging power, the study implements “shallow charging and discharging” with dynamic SOC constraints. The improved PSO algorithm integrates adaptive weighting to overcome local optimal convergence, enhancing global search capabilities and particle migration. Simulation results, based on real-world power plant data, show improved FM accuracy, faster regulation, and reduced energy storage system loss, significantly boosting economic efficiency.
The need for power system frequency management is growing due to the shift in the global energy structure and the steady rise in the share of renewable energy sources [7]. Traditional thermal power units face challenges in meeting the rapidly changing power system scheduling needs because of their large inertia and slow response speed. This is particularly evident when large-scale renewable energy sources are grid-connected, as the power grid experiences more significant frequency fluctuations. Consequently, the engineering and academic communities have begun to focus on the joint frequency regulation (FM) of thermal power units and energy storage systems. This joint FM approach combines the stability benefits of thermal power units with the quick response time of energy storage systems, creating an effective and adaptable FM system that ensures safe and stable power grid operations under a wider range of conditions [14,2].
Energy storage devices play a crucial role in joint FM, not only by increasing FM response times but also by providing additional financial benefits to the power system, such as peak shaving and backup power [9]. However, the introduction of energy storage technologies also brings new financial and technical challenges. The high initial costs of energy storage systems and the significant costs of battery replacement due to aging impose a considerable financial burden on enterprises. Additionally, variables such as the state of charge (SOC) and charging/discharging power directly affect the battery’s service life [16]. While prolonged “full-charge/full-discharge” or “fast-charge/fast-discharge” operations may temporarily enhance FM performance, they significantly reduce battery life over time, leading to increased operational costs. Therefore, optimizing the charging and discharging procedures of energy storage systems to balance FM performance and battery life has become a key area of research.
Recent years have seen significant progress in optimizing energy storage system charging and discharging control mechanisms to address these challenges. Traditional optimization approaches, such as genetic algorithms, dynamic programming, and linear programming, have been widely used. However, these methods often lead to local optima when addressing the multi-coupled complexity of fire-storage joint FM, making it difficult to achieve global optimal solutions. To overcome this limitation, the particle swarm optimization (PSO) algorithm—a group intelligence-based optimization technique—has been gradually applied to energy storage system optimization due to its simplicity, efficiency, and ease of implementation [13]. However, the conventional PSO algorithm can still converge to local optima in multidimensional complex spaces, limiting its global search capability and affecting the efficiency of the optimization results.
To address the shortcomings of the PSO algorithm in energy storage system optimization, this study proposes an adaptive weight-based particle swarm optimization (APSO) algorithm for optimizing the energy storage control strategy of fire-storage joint FM. By introducing an adaptive weighting factor, the algorithm dynamically adjusts the particle migration speed, enhancing its ability to escape local optima and improving the global search’s stability and efficiency [8]. Additionally, this study uses FM speed and accuracy as adaptive evaluation metrics to ensure that the energy storage system not only maintains its response performance but also optimizes its service life and reduces operational costs for enterprises [4,5].
The primary contributions of this paper are as follows:
This paper systematically analyzes the coupling relationship between SOC and charging/discharging power in energy storage systems. It proposes a method for setting charging/discharging power limits based on SOC to prevent “full-charge/full-discharge” operations and achieve “shallow charging and shallow discharging,” effectively extending battery life.
An adaptive weighting-based APSO algorithm is proposed, which dynamically adjusts the weighting factor to improve the algorithm’s global search capability and stability, addressing the local optimization issues of the classic PSO algorithm.
A simulation based on real power plant data is conducted to validate the enhanced algorithm. The results demonstrate that the improved fire-storage joint FM system aligns more closely with the grid dispatch command curve, enhancing the FM effect, prolonging the energy storage system’s service life, and increasing the system’s financial benefits.
The charging and discharging power, state of charge (SOC), and other factors have a direct impact on the lifespan of energy storage batteries. While “full charge and discharge” and “fast charge and discharge” operation modes may temporarily enhance the short-term FM effect of the combined unit, these modes keep the unit in a dispatch state for extended periods. This hinders the ability of the combined unit to respond smoothly to grid demands and significantly reduces the lifespan of the energy storage batteries. In contrast, energy storage system frequency management is better suited for “shallow charging and discharging,” which improves the battery’s lifespan and operational efficiency [6,12].
This paper focuses on the coupling relationship between the SOC and the charging/discharging power of energy storage systems. To achieve the goal of “shallow charging and shallow discharging,” upper and lower SOC bounds are established to prevent “full charge/full discharge” operations. Additionally, the maximum permissible charging and discharging power is determined based on the SOC, as shown in Figure 1. The figure illustrates the concept of “shallow charging and discharging” and its effectiveness in enhancing battery performance and longevity.
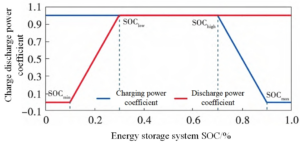
\[\label{e1} SOC_{\text{min}} \leq SOC \leq SOC_{\text{max}}, \tag{1}\] where:
\(SOC\) is the current state of charge of the energy storage system,
\(SOC_{\text{min}}\) is the minimum SOC, typically set to 0.1,
\(SOC_{\text{max}}\) is the maximum SOC, typically set to 0.9.
\[\label{e2} P_{\text{c}} = \begin{cases} P_{\text{c,max}}, & SOC < SOC_{\text{high}}, \\ P_{\text{c,max}} \times \frac{SOC_{\text{max}} – SOC}{SOC_{\text{max}} – SOC_{\text{high}}}, & SOC_{\text{high}} \leq SOC < SOC_{\text{max}}, \\ 0, & SOC \geq SOC_{\text{max}}, \end{cases} \tag{2}\] where:
\(SOC_{\text{high}}\) is the upper SOC limit for charging at rated power,
\(P_{\text{c}}\) is the actual charging power (MW),
\(P_{\text{c,max}}\) is the installed rated charging power (MW).
Power Constraints for Discharging. The discharging power of the energy storage system is limited as follows:
\[\label{e3} P_{\text{d}} = \begin{cases} 0, & SOC < SOC_{\text{min}}, \\ P_{\text{d,max}} \times \frac{SOC – SOC_{\text{min}}}{SOC_{\text{low}} – SOC_{\text{min}}}, & SOC_{\text{min}} \leq SOC < SOC_{\text{low}}, \\ P_{\text{d,max}}, & SOC \geq SOC_{\text{low}}, \end{cases} \tag{3}\] where:
\(SOC_{\text{low}}\) is the lower SOC limit for rated power discharge,
\(P_{\text{d}}\) is the actual discharging power (MW),
\(P_{\text{d,max}}\) is the installed rated discharging power (MW).
The actual charging and discharging power of the energy storage system is limited by its state of charge (SOC) and the maximum permissible charging and discharging power. The energy storage system provides services such as surplus power storage and power gap supplementation, enabling the combined unit to meet grid scheduling demands more effectively. This approach incorporates the energy storage system into the traditional thermal power unit frequency regulation process [10].
When the thermal power unit’s actual production significantly exceeds grid demand, the energy storage system stores the excess electrical energy based on operating conditions. The procedure is described as follows:
\[\label{e4} \begin{aligned} P &= P_{\text{unit}} – P_{\text{c}}, \\ P_{\text{cn}} &= \left| P_{\text{unit}} – P_{\text{AGC}} – P_{\text{zone}} \right|, \\ P_{\text{c}} &= \begin{cases} P_{\text{cn}}, & P_{\text{c,bess}} \geq P_{\text{cn}}, \\ P_{\text{c,bess}}, & \text{otherwise}. \end{cases} \end{aligned} \tag{4}\] Where:
\(P\): Actual power of the combined thermal storage unit FM (MW),
\(P_{\text{cn}}\): Thermal power unit FM response power,
\(P_{\text{c}}\): Actual charging power of the energy storage system (MW),
\(P_{\text{unit}}\): Power system FM dispatching instruction (MW),
\(P_{\text{AGC}}\): Power system dispatching instruction’s dead zone size (MW),
\(P_{\text{c,bess}}\): Maximum permissible charging power of the energy storage system (MW).
When the thermal power unit’s actual production is significantly lower than grid demand, the energy storage system releases stored energy based on operating conditions. The discharging process is described as follows:
\[\label{e5} \begin{aligned} P &= P_{\text{unit}} + P_{\text{d}}, \\ P_{\text{cn}} &= \left| P_{\text{AGC}} – P_{\text{unit}} – P_{\text{zone}} \right|, \\ P_{\text{d}} &= \begin{cases} P_{\text{dn}}, & P_{\text{d,bess}} \geq P_{\text{dn}}, \\ P_{\text{d,bess}}, & \text{otherwise}. \end{cases} \end{aligned} \tag{5}\] Where:
\(P_{\text{d}}\): Actual discharging power of the energy storage system (MW),
\(P_{\text{dn}}\): Response difference between the thermal power unit output and AGC control requirements (MW),
\(P_{\text{d,bess}}\): Maximum permissible discharging power of the energy storage system (MW).
The state of charge (SOC) directly impacts the Depth of Discharge (DOD) and, consequently, the lifetime of the energy storage system. A higher DOD shortens the system’s service life. The relationship between SOC, DOD, and the service life of the energy storage system is expressed as follows:
\[\label{e6} T_{\text{life}} = \frac{L_{\text{DOD}}}{l_{\text{DOD}}}, \tag{6}\] where:
\(T_{\text{life}}\): Actual operational life of the energy storage system (days),
\(L_{\text{DOD}}\): Maximum number of cycles at the specified DOD,
\(l_{\text{DOD}}\): Number of daily cycles at the specified DOD.
The Particle Swarm Optimization (PSO) algorithm mimics the foraging behavior of biological populations [15]. It is designed to find local and global optimal solutions by sharing information among random individuals in the population. Due to its high global convergence, the PSO algorithm is widely applied in system control, model training, and optimization. However, when dealing with multi-coupled complexity problems, the PSO algorithm can easily converge to local optima, limiting its effectiveness [1].
To address these challenges, this study introduces adaptive weights to enhance the power restriction and frequency modulation capabilities of the PSO algorithm, particularly for energy storage charging and discharging.
The adaptability function selects the FM comprehensive performance indicators based on the daily average value of \(K\). This improves the fire-storage joint FM response control, enhances auxiliary service compensation revenue, and evaluates the optimization effect of the energy storage system. The adaptation evaluation function is defined as:
\[\label{e7} \begin{aligned} K &= \frac{K_i \cdot M_i}{\sum M}, \\ K_i &= \max \left( \frac{\left| P_{t+\Delta t} – P_t \right|}{\Delta t \cdot V_{\text{s}}} + \frac{3A_{\text{s}} – \left| P_{t+\Delta t} – P_{\text{aim}} \right|}{A_{\text{s}}}, 0 \right). \end{aligned} \tag{7}\] Where:
\(M\): Mediation mileage vector (MW),
\(K_i\): Integrated performance index of the \(i\) FM process,
\(M_i\): Mediation mileage of the \(i\) FM process,
\(t\): Moment of the AGC instruction (s),
\(t + \Delta t\): Next moment of the AGC instruction (s),
\(P_t\), \(P_{t+\Delta t}\): Combined unit power at moments \(t\) and \(t+\Delta t\) (MW),
\(P_{\text{aim}}\): Target regulation power of the current instruction (MW),
\(V_{\text{s}}\): Standard regulation rate of the combined unit (MW/min),
\(A_{\text{s}}\): Standard regulation accuracy of the combined unit (MW).
In the PSO iterative optimization process, the global optimal particle is the focus of particle population evolution. The development of the particle population around this global optimal particle forms the new particle population [11]. If the global optimal particle falls into a local extreme value field and the current search speed and learning factor are small, the particle population evolution cannot escape this field. This causes the algorithm to converge prematurely, failing to demonstrate its superiority [3].
To address this, we propose an adaptive weight improvement for the PSO particle update method. This method ensures global search capability and algorithm stability by adjusting the particle migration speed coefficient. When the PSO optimization process gets trapped in a local optimum, the new particle position is adjusted to escape the limitation.
The adaptive weight factor is calculated based on the mean fitness value of the current iteration’s particle population and the individual fitness of each particle. If a particle’s fitness value is smaller than the population’s mean fitness, its adaptive weight is larger, indicating a need for global search to find the optimal solution. Conversely, if a particle’s fitness value is larger than the population’s mean, its adaptive weight is smaller, indicating a need for local search to refine the solution. When a particle’s fitness value equals the population’s mean, the adaptive weight is maximized to escape the local optimum. The calculation is shown in Eq. (8):
\[\label{e8} \omega_i = \begin{cases} \omega_{\max}, & y_i < y_{\text{ave}}, \\ \omega_{\min} + \frac{(\omega_{\max} – \omega_{\min}) \cdot (y_{\max} – y_i)}{y_{\max} – y_{\text{ave}}}, & y_i \geq y_{\text{ave}}, \end{cases} \tag{8}\] where:
\(\omega_i\): Inertia factor of particle \(i\) in the current iteration,
\(\omega_{\min}, \omega_{\max}\): Lower and upper bounds of the inertia factor,
\(y_i\): Fitness function value of particle \(i\) in the current iteration,
\(y_{\text{ave}}\): Mean fitness value of the current particle population,
\(y_{\max}\): Maximum fitness value of the current particle population.
New particles are generated randomly around the global optimal solution to form the next-generation particle swarm. The direction and process of the PSO evolutionary search depend on the migration speed, weight factor, and global optimal solution. The particle update equations are shown in Eq. (9):
\[\label{e9} \begin{aligned} P_{i+1,j} &= P_{i,j} + \Delta P_{i+1,j}, \\ \Delta P_{i+1,j} &= \omega V_{i,j} + c_1 \cdot \text{rand}(0,1) \cdot (P_{i,\text{best}} – P_{i,j}) \\ &\quad + c_2 \cdot \text{rand}(0,1) \cdot (P_{\text{g},\text{best}} – P_{i,j}), \end{aligned} \tag{9}\] where:
\(P_{i,j}\): Position of particle \(j\) in generation \(i\),
\(\Delta P_{i+1,j}\): Position change of particle \(j\) in generation \(i\),
\(V_{i,j}\): Velocity of particle \(j\) in generation \(i\),
\(P_{i,\text{best}}\): Best position of particle \(j\) in generation \(i\),
\(P_{\text{g},\text{best}}\): Global best position among all particles,
\(c_1, c_2\): Acceleration coefficients (commonly set to 2),
\(\text{rand}(0,1)\): Random number in the interval \([0,1]\).
The optimization problem for fire-storage joint FM performance can be solved using the adaptive weight PSO algorithm by following these steps:
Step 1 Initialize the particle population with parameters such as population size, initial positions, initial velocities, and evolutionary iterations. Compute the objective function for the initial particle population based on constraints (\({SOC_{\text{high}}}\), \({SOC_{\text{low}}}\)).
Step 2 Update the particle migration speed and position data using the adaptive search algorithm.
Step 3 Evaluate the fitness function for each particle in the current population to identify extreme particles.
Step 4 Compare the global and local optimal solutions for the extreme particles. If the local solution outperforms the global solution, replace the global solution with the local one.
Step 5 Check if the number of evolutionary iterations exceeds the threshold. If so, terminate the process; otherwise, return to Step 2.
This procedure ensures that the fire-storage joint FM optimization is robust, efficient, and capable of avoiding local optima traps, resulting in improved system performance and reliability.
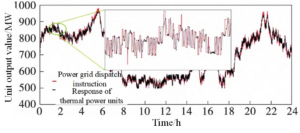
Figure 2 illustrates the sampling interval of 1 s and the selection of 24-hour real operation data of a 1,050 MW thermal power unit from a power plant. An energy storage system with an installed capacity of 15 MW/7.5 MW-h is included in the simulation. The primary function of the energy storage system is to assist the thermal power units in meeting the demand for grid frequency regulation. To determine the optimal charge capacity thresholds of the energy storage system (\(SOC_{\text{high}}\) and \(SOC_{\text{low}}\)), the revised PSO algorithm uses a particle swarm size of 20, a maximum of 100 evolution generations, and adaptive weights that dynamically change with the fitness function.
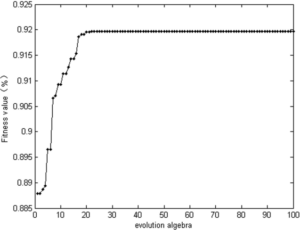
Using the adaptive weight PSO optimization iteration, the integrated performance index of the combined fire-storage FM’s ideal solution is obtained. Figure 3> displays the evolution curve of the adaptation degree, while Figure 4 shows the simulation curve for the joint operation of fire and storage.
A comparison of the curves in Figure 2 and Figure 4 demonstrates that the enhanced combined fire-storage FM response trend better aligns with the grid FM dispatch command curve, significantly improving the FM response effect. According to the global optimal results, the combined fire-storage FM’s average daily comprehensive FM performance index reaches the optimal value of 4.12, and the optimal set points for \(SOC_{\text{high}}\) and \(SOC_{\text{low}}\) are 57.5% and 42.5%, respectively. The joint operation of the energy storage system and thermal power unit improves adherence to grid FM dispatch instructions.
The FM comprehensive performance index increased by 0.08 compared to the previous version. The enhanced energy storage system generates approximately 35 million yuan in additional annual revenue under the following assumptions:
A year of joint FM operation for fire storage consists of 360 days,
A single FM compensation is valued at 0.6 yuan/MW,
The average daily response to grid scheduling is set at 20,000 MW.
Furthermore, the typical daily cycle times of the energy storage system decreased from approximately 10 cycles before optimization to approximately 9.5 cycles after optimization. By using advanced lithium titanate batteries capable of up to 25,000 charging and discharging cycles, the service life of the energy storage equipment is extended to approximately 88 days. This method enhances the system’s efficiency and partially offsets the investment cost of the energy storage system.
This study introduces an adaptive weighting factor to dynamically adjust the particle migration speed within the standard particle swarm optimization (PSO) framework, addressing the problem of local optima. The proposed adaptive PSO (APSO) algorithm improves the global search capability and algorithm stability.
Simulation experiments confirm that the modified APSO algorithm significantly enhances the fire-storage joint FM system’s regulation speed and accuracy. The FM response more closely aligns with the grid scheduling command curve. Results from the simulation demonstrate that the optimized fire-storage joint FM system:
Increases the annual revenue of the energy storage system,
Extends the service life of energy storage equipment,
Improves economic benefits and utilization efficiency,
Reduces energy storage system losses while meeting FM demand.
The proposed APSO algorithm provides a robust, efficient solution for optimizing fire-storage joint FM systems, achieving a balance between performance improvement and cost-effectiveness.