The Cascaded Integrator Comb (CIC) decimation filter is a pivotal technology extensively employed in digital signal processing (DSP). This paper delves into a comprehensive examination of the CIC algorithm within software-defined radio (SDR) systems from the perspective of parallel computing and introduces a novel Non-Recursive Implementation (NR-I) on an NVIDIA GPU using CUDA. The NR-I approach significantly reduces computational load by unfolding the recursive CIC structure with pre-derived Unfold Factors. Further optimization was achieved through data-transfer enhancements using PM Implementation (PM-I) and ODT Implementation (ODT-I). Experimental results demonstrate that NR-I achieves a speedup of over 449.48. Additionally, the data-transfer optimizations resulted in substantial performance improvements, with PM-I and ODT-I reducing execution time by 43.24% and 64.22%, respectively. The GPU implementation’s speedup is significantly greater than that of OpenMP, ranging from 3.34 to 10.22 times. These results underscore the effectiveness of the proposed Non-Recursive Implementation in accelerating time-intensive and data-intensive computations.
The CIC decimation filter is a digital multirate filter used for managing substantial sample rate changes in DSP systems [13]. Its highly symmetric structure enables efficient implementation, leading to its widespread application across various DSP domains [2]. This paper aims to examine and propose a high-performance software algorithm for implementing the CIC filter in an SDR system.
The CIC algorithm is extensively employed in various SDR applications, including digital down converters (DDCs), digital up converters (DUCs), sample rate conversion (SRC) systems, and both transmission and reception systems, among others. Additionally, researchers have focused significantly on software implementation and optimization techniques. These approaches can be broadly categorized based on the underlying technology, including Digital Signal Processor (DSP) implementations, Field Programmable Gate Array (FPGA) implementations, Universal Software Radio Peripheral (USRP) implementations, and multi-core CPU parallel implementations.
DSP represents a specialized microprocessor, tailored explicitly for executing digital signal processing duties. In the context of CAI SS’s research, a DDC framework leveraging DSP technology was developed and deployed, resulting in substantial enhancements to both the performance and adaptability of communication systems.
FPGA, on the other hand, constitutes an integrated circuit architecture that allows for in-field customization by programming professionals. Numerous prior endeavors have delved into this domain, including the work of Datta et al. [7], who concentrated on a configurable CIC decimator endowed with pruning features aimed at minimizing hardware resource consumption. Furthermore, by employing partitioning strategies within the decimator factor, a notable reduction in computational latency can be achieved.
The Universal Software Radio Peripheral (USRP) finds ubiquitous application in the realm of Software-Defined Radio (SDR) [8,1], serving as a versatile and cost-effective transceiver that transforms standard hosts into potent wireless prototyping platforms [15]. Kodali R K et al. [12] delved into the intricacies of CIC and various other filter types employed in Direct Digital Conversion (DDC) and Direct Up Conversion (DUC) processes, offering insights into their utilization across diverse USRP platforms.
Multi-core Central Processing Units (CPUs) have gained widespread adoption across myriad application domains, SDR being no exception. These CPUs, collectively, possess the capability to concurrently execute multiple instructions, enhancing overall efficiency. OpenMP, a prevalent shared memory parallel programming interface, provides high-level constructs that have been extensively employed in SDR endeavors [3], facilitating seamless parallel execution.
In recent times, General-Purpose computing on Graphics Processing Units (GPGPU) has emerged as a potent means of tackling DSP algorithms [14,4,19]. Given their exceptional data and thread parallelism, immense computational prowess, and relatively low cost, GPGPUs have garnered significant attention for executing time- and data-intensive algorithms. NVIDIA’s introduction of the CUDA development environment in 2007 further propelled GPU computing by establishing a general-purpose parallel computing architecture that simplifies and accelerates programming efforts [5]. As a viable acceleration method, GPUs offer the dual advantage of FPGA’s high-performance capabilities and the flexibility of general-purpose programming languages, making them suitable for supporting real-time SDR systems. Prior research has explored the feasibility of GPU-accelerated DSP algorithms [16,11], yet, to the best of our knowledge, no study has specifically targeted the CIC algorithm within an SDR context and addressed its implementation on GPUs.
In this work, we conducted an exhaustive analysis of the CIC algorithm with a focus on its GPU-based implementation. Specifically, we introduced the R-I approach for executing the CIC decimation filter on the GPU, followed by the Novel NR-I method aimed at enhancing performance. A comparative assessment between R-I and NR-I revealed that the latter exhibited significantly superior performance. To delve deeper into optimization, we elaborated on practical strategies for optimizing data transfers. Additionally, we presented the sequential CPU version and OpenMP-based implementation as benchmark tests to quantify the overall speedup achieved by our CIC algorithm implementation.
Over two decades ago, Eugene B. Hogenauer first introduced this concept [10], which has since been employed for both interpolation and decimation purposes [9]. Notably, it boasts a multiplier-free architecture, requiring minimal memory and hardware complexity, comprising solely of adders and delay elements. The CIC filter’s low power consumption is a significant advantage, making it a popular choice in digital down converters (DDC) and digital up converters (DUC) [6]. Essentially, the CIC filter’s primary functions involve adjusting sampling rates, either by decreasing them (decimation) or increasing them (interpolation). Typically, the CIC structure is comprised of multiple ideal integrator and comb filter stages [17].
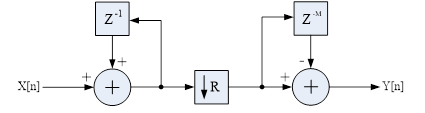
Figure 1 displays the primary architecture of a single-stage CIC decimation filter, comprising a pair of integrator and comb filters, with a down-sampling unit interposed between them. Considering \(f_{s}\) as the sampling frequency within the integrator section, the down-sampling unit processes the signal to produce a lower sampling rate of \(f_{s}\)/\(R\), which then serves as the input sequence for the comb section. For a given data sequence \(S\), the integrator section aims to determine the output sequence \(S'\) in accordance with the prescribed equation. \[\label{1)} S'\left[n\right]\quad =\quad S'\left[n-1\right]+S\left[n\right] . \tag{1}\]
The equation for the comb-section can be formulated as given in Eq. (2), where the output sequence \(O\) is solely determined by three integer parameters: R, D and N. These parameters correspond to the decimation ratio, the differential delay (commonly 1, but occasionally 2), and the number of stages in the filter, respectively. \[\label{2)} O\left[n\right]\quad =\quad S'\left[n\right]-S'\left[n-RD\right] . \tag{2}\]
By integrating Eq. (1) and Eq. (2), the combined integrator-comb section can be mathematically represented as Eq. (3). \[\label{3)} O\left[n\right]= \sum _{k=0}^{RD-1}S\left[n-k\right] = O\left[n-1\right]+S\left[n\right]-S\left[n-RD\right]. \tag{3}\]
Typically, a CIC decimation filter incorporates multiple stages, and the realization of an N-stage CIC filter follows a recursive approach. Each stage’s objective is encapsulated in Eq.(3). For a given sequence of length L, the CIC filter’s task involves deriving a sequence O of length L/RD. The recursive process of an N-stage CIC filter is outlined in Algorithm 1, encompassing two distinct phases: the cascaded integrator-comb phase and the decimation phase. During the first phase, the process adheres to Eq. (3), where the output sequence from one stage serves as the input for the subsequent stage in an N-stage CIC configuration. Subsequently, the decimation process selects one input sample for every RD output samples, resulting in an output sequence O with a length of L/RD.

NVIDIA unveiled the CUDA development environment in 2007, establishing a universal parallel computing platform and programming interface paradigm that significantly enhances the efficiency and accessibility of GPU computing. As depicted in Figure 2, the CUDA architecture and programming model encompass two distinct code types: host-side code, executed on the CPU, and device-side code, executed on the GPU. This parallel execution on the GPU intertwines with serial execution on the CPU. On the device side, threads are structured in a three-tiered hierarchy: grids, blocks, and threads. Memory, meanwhile, is categorized into six types: Registers, Local Memory, Shared Memory, Global Memory, Constant Memory, and Texture Memory.
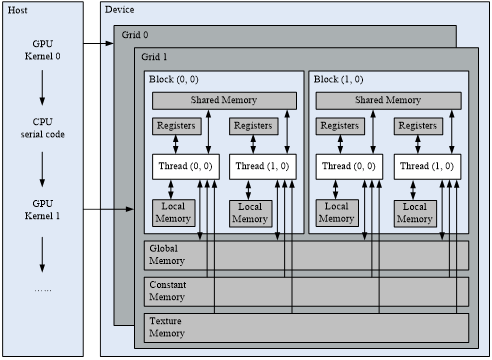
In the CUDA programming model, the fundamental execution unit on the device side is the thread. These threads can be grouped into thread blocks, which form a cohesive unit capable of efficient data sharing and intercommunication via shared memory. However, cooperation between threads belonging to different blocks is hindered by the need for complex synchronization mechanisms. Similarly, thread blocks can be assembled into grids, where each grid executes the same kernel. Nevertheless, threads in separate blocks within the same grid cannot directly communicate with each other.
On the host side, the basic execution unit in the CUDA programming model is referred to as a kernel. When a CUDA program initiates a kernel on the host, the thread blocks within the grid are enumerated and dispatched to multiprocessors with available computational resources. This allows for the parallel execution of all threads within the grid [20].
In this section, we initially discuss the block-based computational method for managing extensive signal data over prolonged durations. Subsequently, we individually introduce the core concepts and implementation details of the Recursive Implementation (R-I) and the Non-Recursive Implementation (NR-I). To conclude, we briefly touch upon the subject of optimizing data transfer processes.
Tackling the challenge of processing lengthy signals is a common endeavor in signal processing, often addressed by transforming extensive data-sequence computations into manageable block-wise calculations. This involves partitioning the input data-sequence into segments, each of which can be individually processed. Assuming that the extensive signal sequence is segmented into length-N data blocks, the k-th segment, denoted as \(S_{k}\), is represented by Eq.(4). \[\label{4)} S_{k} {\rm =}\left\{s\left[k*N\right],\; s\left[k*N+1\right],\; \cdots ,\; s\left[\left(k+1\right)*N-2\right],\; s\left[\left(k+1\right)*N-1\right]\right\} . \tag{4}\]
As depicted in Eq. (1) through (3), during the initial CIC stage, the computation of the element \(s\left[k*N\right]\) necessitates the utilization of RD-1 additional data items from the preceding segment to determine the corresponding O value. For multi-stage CIC implementations, the quantity of required data items from the prior segment surpasses RD-1. Consequently, it is imperative for the algorithm’s execution to account for data dependencies to avoid incorrect output results from block-based computations. To address this challenge, we have employed an overlap-save mechanism in this paper. To facilitate understanding, we have outlined the notations utilized in the GPU-based implementation of CIC in Table 1.
| Notation | Explanation |
| \(S\) | Input data-sequence |
| \(O\) | Output data-sequence |
| \(L_I \) | Input data length |
| \(L_B \) | Data segment size for single block processing |
| \(L_O \) | Overlap prefix length in CIC kernel execution |
| \(R\) | Decimation ratio |
| \(D\) | Differential delay |
| \(N\) | Number of stages |
| \(UF\) | Unfold Factors in NR-I |
| \(NT\) | Thread count per block in CUDA configuration |
| \(NB\) | Block count in CUDA programming model |
| \(NB_IC \) | The number of blocks in CUDA for the CIC Integrator-Comb pair kernel |
| \(NB_DE \) | The number of blocks in CUDA for the CIC decimation kernel |
Addressing the task of filtering a lengthy signal data-sequence \(S\) within an overlap-save framework, it is necessary to segment S into smaller data blocks, each with a length denoted as \(L_{B}\). As previously noted, additional input samples from the preceding segment (k-1) are required to process segment k. Assuming the overlap length in the previous segment is \(L_{O}\), it follows that \(L_{I}\) data items are necessary to process a segment of length \(L_{B}\) . In simpler terms, the input sequence length \(L_{I}\) equates to the sum of \(L_{B}\) and \(L_{O}\). Regarding the N-stage CIC decimation filter, the initial CIC stage outcome \(O\left[k\right]\) can be calculated using Eq. (5), which incorporates \(S\left[k\right]\) along with RD-1 additional data items. Specifically, the most preceding data item required is \(S\left[k-RD+1\right]\). \[\label{5)} O\left[k\right]=O\left[k\right]+O\left[k-1\right]+…+O\left[k-RD+1\right] . \tag{5}\]
Building upon the aforementioned foundation, during the second CIC stage, \(O\left[k\right]\) can likewise be computed using Eq. (5), albeit with a crucial distinction: the \(S\left[k-RD+1\right]\) mentioned here corresponds to \(O\left[k-RD+1\right]\) from the preceding CIC stage. Analogously, \(O\left[k-RD+1\right]\) necessitates RD-1 preceding data items prior to the index \(k-RD+1\). Consequently, the first CIC stage necessitates RD-1 additional data items, while the second stage requires a total of \(2*\left(RD-1\right)\) data items. This trend can be extrapolated, with each subsequent stage demanding an additional RD-1 previous data items. In conclusion, for an N-stage CIC decimation filter characterized by parameters R and D, the prefix data length for overlap across the CIC stages can be formulated as follows. \[\label{6)} L_{O} =\left(RD-1\right)*N . \tag{6}\]
To facilitate the execution of CIC on a GPU, the data subject to processing must be transferred to the GPU’s global memory and subsequently dispersed among multiple thread blocks for computation. Nevertheless, a primary challenge lies in the absence of CUDA mechanisms that permit inter-block thread synchronization, rendering recursive CIC application within a single kernel launch impractical. To overcome this limitation, the aforementioned two-phase CIC process must be implemented discretely, with the cascaded integrator-comb phase and the decimation phase handled and invoked independently.
To embed the CIC process within the GPU architecture, the R-I approach is introduced. This implementation comprises two distinct kernels, tailored to execute the functionalities of the integrator-comb phase and the decimation phase, respectively. Specifically, for the cascaded integrator-comb phase, a CUDA kernel titled CIC_IC_Kernel is devised to encapsulate the single CIC integrator-comb operation. When dealing with an N-stage CIC process, the desired effect is achieved by sequentially invoking the CIC_IC_Kernel N times. As shown in Algorithm 2.

During the downsampling or decimation phase, the corresponding GPU-oriented implementation is outlined in Algorithm 3. The primary objective of this decimation process is to extract a single output sample for every RD input samples, thereby reducing the length of the output array \(O\) to \(L\)/\(RD\) subsequent to the decimation operation.

The execution strategy for launching the CIC kernels is detailed in Algorithm 4. When tackling an N-stage CIC process, the cascaded integrator-comb phase is implemented by iteratively launching the CIC Integrator-Comb kernel N times. Following each kernel launch, the output generated from the preceding stage serves as the input sequence for the subsequent stage. Subsequently, the decimation phase is enacted by invoking the CIC decimation kernel.

As outlined in the preceding section, to achieve the effect of N-stage CIC process, the recursive CIC algorithm was proposed. However, launching CUDA kernel frequently will have a certain impact on the performance of the algorithm. For more optimization, we studied the multi-stage structure of CIC algorithm in depth, and proposed a Non-recursive CIC algorithm on GPU. Algorithm 1 reveals that the multiple stages CIC implementation in C language is the structure of two-layer for-loop. For simplicity, we explain the 2-stage CIC process with parameters R=2 and D=1, assume \(S\) is the input data-sequence with items \(S\left[1\right]\), \(S\left[2\right]\), …, \(S\left[n\right]\), then define \(O_{1}\) and \(O_{2}\) as the output sequence in the first and second CIC stage. According to Algorithm 1, \(O_{1} \left[n\right]\) is equal to \(S\left[n\right]\)+\(S\left[n-1\right]\); likewise, \(O_{2} \left[n\right]\) is equal to \(O_{1} \left[n\right]\)+\(O_{1} \left[n-1\right]\), and it can be further expressed as \(S\left[n\right]\)+\(2S\left[n-1\right]\)+\(S\left[n-2\right]\).
From the demonstration procedure described above, it is not hard to draw the conclusion that, in the 2-stage CIC structure with parameters R=2 and D=1, for any item \(S\left[k\right]\), the relative CIC result \(O_{2} \left[k\right]\) can be expressed as \(S\left[k\right]\)+\(2S\left[k-1\right]\)+\(S\left[k-2\right]\), a set of weighting coefficients [1, 2, 1] can be found out to present the non-recursive CIC structure. According to its principle of generating, UF can be pre-derived as described in Algorithm 5.

Algorithm 6 introduces a non-iterative approach for implementation. As previously mentioned, in the context of an N-stage CIC decimation filter, the computation of \(O\left[k\right]\) in the N-stage CIC necessitates the preceding \(L_{O}\) data elements. Consequently, the non-iterative formulation can be formulated as follows. Here, we designate UF as the Unfolding Factors pertaining to the CIC. \[\label{7)} O\left[k\right]=S\left[k\right]*UF\left[0\right]+S\left[k-1\right]*UF\left[1\right]+…+S\left[k-L_{O} +1\right]*UF\left[L_{O} \right] . \tag{7}\]
Assuming a CUDA configuration with NT threads per block, given that only \({L_{B} \mathord{\left/ {\vphantom {L_{B} RD}} \right. } RD}\) data elements need to be processed, the number of thread blocks NB can be calculated as \(NB={\left({L_{B} \mathord{\left/ {\vphantom {L_{B} RD}} \right. } RD} \right)\mathord{\left/ {\vphantom {\left({L_{B} \mathord{\left/ {\vphantom {L_{B} RD}} \right. } RD} \right) NT}} \right. } NT}\). Furthermore, since the length of the input sequence exceeds the number of threads by a factor of RD, the mapping between the data index and the thread index is specified in Eq. (8). It is important to note that after the CIC stage, the length of the output is reduced to \({1\mathord{\left/ {\vphantom {1 RD}} \right. } RD}\) of the original input length. \[\label{8)} I_{R} =idx*RD+L_{O} . \tag{8}\]

Within the realm of GPU parallel computing acceleration frameworks, efficiently transferring data between the system RAM and GPU’s VRAM is paramount, as it significantly impacts overall performance [18]. Analysis of execution times reveals that data transfer accounts for 77.21% to 87.76% of the total time in the non-recursive implementation (NR-I), underscoring its status as a major bottleneck. To mitigate this, two strategies were employed to minimize data transfer delays between the host and device: employing pinned memory instead of pageable memory (PM-I), and overlapping kernel execution with data transfer (ODT-I).
When allocating CPU memory destined for GPU processing, a choice exists between pageable and pinned memory. In scenarios where data is transferred from pageable host memory to device memory, pinned memory typically serves as an intermediary, adding unnecessary overhead and hindering performance. PM-I circumvents this by directly allocating host memory as pinned, eliminating the need for an intermediate transfer step. Analysis shows that PM-I enhances performance by a factor of 1.76 compared to NR-I.
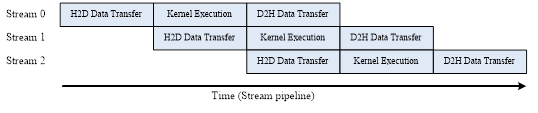
The conventional GPU workflow involves sequential steps: transferring data from host to device, executing kernels, and transferring results back to host. This serial approach hinders concurrency. To address this, we leveraged CUDA streams to organize multiple CIC processes into workflows, enabling concurrent execution of data transfer and kernel operations. By structuring operations into streams, independent kernels can execute in a pipelined fashion, as illustrated in Figure 3. Our analysis indicates that ODT-I further reduces execution time by 35% to 60% when applied in conjunction with PM-I.
In this segment, we commence by outlining the experimental configuration in a concise manner. Subsequently, we delve into a comparative analysis of the speed enhancements achieved by the Recursive Implementation (R-I) and the Non-Recursive Implementation (NR-I). Following this, we present the experiments conducted to optimize data transfer processes. Lastly, we conclude with an overview of the comprehensive speedup experiments that were undertaken.
To thoroughly assess the efficacy of our proposed GPU-accelerated implementation, a comprehensive experimental framework is established. In addition to the GPU-based implementation of the CIC algorithm, we also develop its sequential CPU counterpart and an OpenMP-parallelized version utilizing 32 threads, allowing for a side-by-side performance comparison and validation of the achieved acceleration.
In terms of hardware, the experiments are executed on a high-performance computing (HPC) server, equipped with a potent Intel Xeon E5-2650 v2 CPU featuring dual processors, each comprising 16 cores capable of executing 32 threads concurrently, operating at a base frequency of 2.6 GHz with a core speed of 1.2 GHz. Complementing this setup, a NVIDIA Tesla k20c GPU is utilized, boasting 2496 CUDA cores organized across 13 Streaming Multi-Processors (SMs), 2 GB of dedicated RAM, a processor clock speed of 1059 MHz, a memory clock speed of 900 MHz, and an impressive memory bandwidth of 28.8 GB/s.
On the software side, the experimental setup is anchored on the Windows Server 2008 R2 Enterprise x64 operating system. The CUDA Toolkit version utilized is 7.0, while the OpenMP environment is configured with version 4.5, ensuring compatibility and optimal performance for the parallel computations involved.
To assess and contrast the efficacy of the introduced R-I and NR-I methods, we designed and executed three experimental groups. In the control group, we executed the sequential CPU implementation across a range of problem sizes, meticulously documenting the execution times. Subsequently, we evaluated both the recursive and non-recursive CIC kernels on the GPU, meticulously tracking both the memory management time (inclusive of allocation, transfer, and deallocation durations) and the GPU execution time. Our analysis encompasses both these individual times and the overall execution time, which comprehensively accounts for both memory management and GPU computation phases.
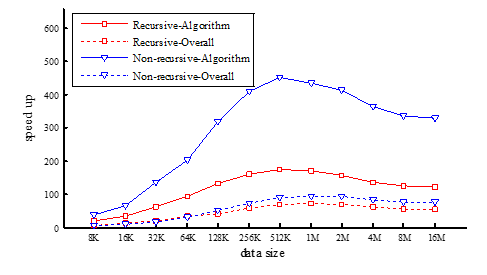
Table 2 presents the execution times and acceleration factors of R-I and NR-I, with millisecond serving as the time unit. Let CPU execution time be denoted as CPU-EXE, GPU kernel execution time as GE, memory management time as MM, and overall execution time as OE (OE = GE + MM). The GPU implementation speedups (SP_G) signify the ratios of CPU-EXE to GE, while the overall process speedups (SP_O) represent the ratios of CPU-EXE to OE. It is important to note that the CIC filter is configured with a stage of 5 and a decimation ratio of 8, and 12 distinct problem sizes are examined. Figure 4 visually depicts the algorithm and overall speedups achieved by R-I and NR-I. As evident from Figure 4, the speedups of R-I and NR-I across varying problem sizes (ranging from 8K to 16M) lie between 18.34 and 174.74, and 35.55 to 449.48 respectively, clearly indicating that NR-I outperforms R-I, with its algorithm speedup being approximately 1.9 to 2.7 times higher.
| CPU-EXE | Recursive | Non-recursive | |||||||
| MM | GE | SP_G | SP_O | MM | GE | SP_G | SP_O | ||
| 8K | 2.4093 | 0.2967 | 0.1313 | 18.34 | 5.63 | 0.4787 | 0.0678 | 35.55 | 4.41 |
| 16K | 4.8183 | 0.3092 | 0.1401 | 34.39 | 10.72 | 0.5032 | 0.0743 | 64.84 | 8.34 |
| 32K | 9.7390 | 0.3315 | 0.1601 | 60.85 | 19.81 | 0.5205 | 0.0726 | 134.15 | 16.42 |
| 64K | 19.377 | 0.3860 | 0.2057 | 94.20 | 32.75 | 0.5720 | 0.0965 | 200.86 | 28.99 |
| 128K | 39.0872 | 0.6550 | 0.2974 | 131.43 | 41.04 | 0.6710 | 0.1229 | 318.05 | 49.24 |
| 256K | 77.6370 | 0.8672 | 0.4905 | 158.29 | 57.18 | 0.8756 | 0.1897 | 409.29 | 72.88 |
| 512K | 149.9924 | 1.3108 | 0.8584 | 174.74 | 69.15 | 1.3578 | 0.3337 | 449.48 | 88.67 |
| 1M | 269.6571 | 2.1801 | 1.5686 | 171.91 | 71.93 | 2.2428 | 0.6196 | 435.22 | 94.21 |
| 2M | 465.6863 | 3.8564 | 2.9829 | 156.12 | 68.09 | 3.9411 | 1.1273 | 413.09 | 91.88 |
| 4M | 791.5175 | 7.3286 | 5.8286 | 135.80 | 60.16 | 7.4728 | 2.1719 | 364.44 | 82.07 |
| 8M | 1429.0720 | 14.7735 | 11.4980 | 124.29 | 54.40 | 14.782 | 4.2463 | 336.55 | 75.10 |
| 16M | 2749.3795 | 28.3771 | 22.8279 | 120.44 | 53.69 | 28.3835 | 8.3797 | 328.10 | 74.79 |
However, it is noteworthy that the overall speedups are substantially lower than the algorithm speedups. This disparity stems primarily from the substantial contribution of memory management time to the total execution time. As reflected in Table 2, the data transfer times for R-I and NR-I constitute a significant portion of the total execution time, accounting for 55.4% to 69.3% and 77.21% to 87.76% respectively.
Additionally, we have delved into the reasons behind the decrease in performance graphs beyond 512K. In our experiments, the problem sizes were doubled consecutively. If the execution time scaled linearly with the problem size, the execution time for the next size would theoretically be twice that of the previous. We define TR as the ratio of execution times between consecutive problem sizes, with an ideal value of 2. Our findings indicate that the TRs for CPU implementations hovered around 2 but experienced a slight downturn post-512K. Conversely, the TRs for GPU implementations gradually increased from 1 towards 2 and eventually stabilized at approximately 2, signifying enhanced GPU performance with increasing problem sizes. Ideally, if CPU TRs remained constant at 2, the graphs would progressively rise and stabilize. However, the slight decline in CPU TRs beyond 512K (implying improved CPU performance post-512K, contrary to the ideal constant) is precisely what accounts for the decline observed in the graphs presented in Figure 4.
As aforementioned, data transfer emerges as the primary performance hindrance. To mitigate this, PM-I and ODT-I strategies were implemented. To assess and contrast their impact on accelerating data transfer, three experimental sets were undertaken, with outcomes summarized in Table 3.
| NR-I | PM-I | ODT-I | |||||
| Time | Time | Reduction (%) | SP | Time | Reduction (%) | SP | |
| 8K | 0.5376 | 0.5521 | -2.70 | 0.97 | 0.2260 | 57.97 | 2.38 |
| 16K | 0.5620 | 0.5647 | -0.47 | 1.00 | 0.2251 | 59.96 | 2.50 |
| 32K | 0.6178 | 0.5565 | 9.93 | 1.11 | 0.2366 | 61.70 | 2.61 |
| 64K | 0.6937 | 0.5787 | 16.57 | 1.20 | 0.2971 | 57.16 | 2.33 |
| 128K | 0.8299 | 0.7120 | 14.20 | 1.17 | 0.4473 | 46.10 | 1.86 |
| 256K | 1.2639 | 0.8137 | 35.62 | 1.55 | 0.5284 | 58.20 | 2.39 |
| 512K | 1.6713 | 1.2207 | 26.96 | 1.37 | 0.7415 | 55.63 | 2.25 |
| 1M | 2.8349 | 1.9891 | 29.84 | 1.43 | 1.1737 | 58.60 | 2.42 |
| 2M | 5.0118 | 3.2258 | 35.64 | 1.55 | 2.0608 | 58.88 | 2.43 |
| 4M | 9.5911 | 5.7642 | 39.90 | 1.66 | 3.6616 | 61.82 | 2.62 |
| 8M | 19.0699 | 10.8709 | 42.99 | 1.75 | 6.8241 | 64.22 | 2.79 |
| 16M | 36.8110 | 20.8924 | 43.24 | 1.76 | 13.1794 | 64.20 | 2.79 |
This table outlines the comprehensive execution times (encompassing memory management and GPU processing) for NR-I, PM-I, and ODT-I across varying problem sizes. It also presents the percentage reductions in execution time and speedups achieved by the optimized data transfer implementations (PM-I and ODT-I). The data in Table III underscores that for larger problem sizes (exceeding 128K data points), GPU-based implementations yield substantial acceleration gains. Compared to NR-I, the optimized methods, PM-I and ODT-I, achieve noteworthy improvements, with PM-I reducing execution time by over 43.24% and ODT-I by over 64.22%. Specifically, PM-I achieves a 1.76x speedup, while ODT-I attains a 2.79x speedup. These findings affirm that the adopted data transfer optimization techniques effectively bolster practical performance.
To assess the comprehensive speedup achieved by CIC, we executed three sets of experiments across varying problem sizes. The total execution time encompasses kernel execution, data transfer, and additional processing durations. To benchmark the overall speedup of CIC, we initially presented a sequential CPU implementation as a comparative baseline. Nevertheless, acknowledging that a GPU implementation inherently surpasses a sequential CPU counterpart, it is imperative to broaden the comparison scope beyond just a sequential algorithm. Thus, we also implemented an OpenMP version of CIC, enhancing the optimization analysis’s significance. Essentially, both GPU and OpenMP leverage the SIMD (Single Instruction, Multiple Data) paradigm. While a GPU can spawn thousands of threads, each concurrently updating a vector element, OpenMP’s thread allocation is constrained by the physical processor’s capabilities. Given the Intel Xeon E5-2650 v2 CPU’s 16 cores and 32 threads, we maximized the parallel region’s thread count to 32, ensuring optimal CPU utilization.
| CPU-Time | OpenMP#32 | ODT-I | ||||
| Time | SP-CPU | Time | SP-CPU | SP-OMP | ||
| 8K | 2.4093 | 0.7543 | 3.19 | 0.2260 | 10.66 | 3.34 |
| 16K | 4.8183 | 0.8573 | 5.62 | 0.2251 | 21.41 | 3.81 |
| 32K | 9.7390 | 1.1014 | 8.84 | 0.2366 | 41.16 | 4.66 |
| 64K | 19.377 | 1.4552 | 13.32 | 0.2971 | 65.22 | 4.90 |
| 128K | 39.0872 | 2.0521 | 19.05 | 0.4473 | 87.38 | 4.59 |
| 256K | 77.6370 | 3.2156 | 24.14 | 0.5284 | 146.93 | 6.09 |
| 512K | 149.9924 | 5.2231 | 28.72 | 0.7415 | 202.28 | 7.04 |
| 1M | 269.6571 | 9.5148 | 28.34 | 1.1737 | 229.75 | 8.11 |
| 2M | 465.6863 | 18.0432 | 25.81 | 2.0608 | 225.97 | 8.76 |
| 4M | 791.5175 | 34.8946 | 22.68 | 3.6616 | 216.17 | 9.53 |
| 8M | 1429.0720 | 68.412 | 20.89 | 6.8241 | 209.42 | 10.03 |
| 16M | 2749.3795 | 134.7377 | 20.41 | 13.1794 | 208.61 | 10.22 |
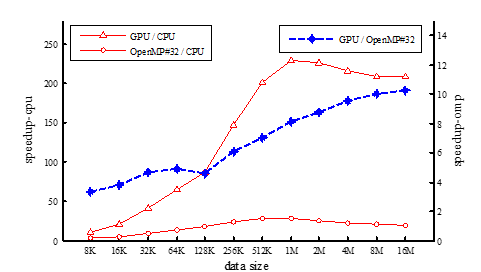
Table 4 details the comprehensive execution times and acceleration factors across varying problem sizes. Each row showcases the experimental problem size, alongside the execution times for the CPU (CPU-time), OpenMP (with 32 threads) implementation and its respective speedup vis-à-vis the CPU, as well as the GPU execution time and its speedups compared to both the CPU and OpenMP (32 threads) implementations. Figure 5 visually depicts these speedups, highlighting a discernible trend: the overall speedup generally escalates with an increase in problem size, peaking at over 229.75.
Concurrently, the OpenMP implementation, when compared to the sequential CPU version, demonstrates a notable acceleration effect, achieving maximum speedups exceeding 28.72. Nevertheless, the GPU implementation, when juxtaposed against the OpenMP (32 threads) variant, emerges as the more potent accelerator, exhibiting speedups that far surpass those of OpenMP, ranging approximately from 3.34 to 10.22 times. These experimental findings underscore the substantial acceleration gains afforded by the GPU implementation.
The CIC decimation filter is an important component which is extensively used in DSP, to enable the software CIC decimation filter to real-time processing the massive digital signal data, two kinds of GPU based implementations are subsequently proposed: R-I and NR-I. Benefiting from the tremendous computational power of GPU, the GPU based CIC implementations gain huge performance improvements, the algorithm speedups of the R-I and NR-I achieve more than 174.74 and 449.48. The speedup of NR-I is about 1.9-2.7 times than the corresponding recursive one, it validates that the Non-recursive structure based CIC which proposed in this paper can reduce the computational burden in much degree and achieve more performance. As data-transfer has become the overall performance bottleneck, the PM-I and ODT-I were applied for further optimization, the results confirmed that the data-transfer optimization approaches effectively enhance the performance in practice. To assess the overall speedup of the GPU-based CIC, both the sequential CPU implementation and the OpenMP implementation were used for comparison. The GPU implementation achieves a speedup of over 229.75 times compared to the CPU version. When compared to the OpenMP implementation, which uses 32 threads, the GPU version demonstrates even greater acceleration, with speedups ranging from approximately 3.34 to 10.22 times. These findings lead to the conclusion that the GPU-based implementation and optimization of software CIC offer substantial performance improvements over the CPU-based approach, particularly in scenarios that are both time- and data-intensive.
This work was supported in part by National Natural Science Foundation of China (Grant No. 62362049, 62402205, 62262023), Natural Science Foundation of Jiangxi Province of China (Grant No. 20232BAB212009), the Key Laboratory of Data Protection and Intelligent Management, Ministry of Education, Sichuan University (Grant No. SCUSAKFKT202307Y), the Jiangxi Provincial Key Laboratory of Data Security Technology(Grant No. 2024SSY03181), the Finance Science and Technology Special “Contract System” Project of Jiangxi Province (Grant No. ZBG20230418014).