Contents

Utilitas Mathematica

  • Research article

Decoding Nonsteroidal Anti-inflammatory Drugs with Sombor Invariants: A Quantum Leap in QSPR Modeling

Abaid ur Rehman Virk1, Muhammad Usman2
1Department of Mathematics, University of Management and Technology, Lahore, Pakistan
2Department of Mathematics, Government College University, Lahore, Pakistan
  • Received: 11/12/2023
  • Accepted: 27/02/2024
  • Published: 31/03/2024

Abstract

We investigate the Sombor indices for a diverse group of nonsteroidal anti-inflammatory drugs (NSAIDs) to understand their molecular architecture and physicochemical properties. By utilizing quantitative structure-property relationship (QSPR) modeling, we establish mathematical models linking Sombor indices to key pharmacodynamic and toxicological parameters. Our study sheds light on how the molecular composition of NSAIDs influences their drug profiles and biological behavior, offering valuable insights for drug development and safety assessment.

Keywords: Nonsteroidal anti-inflammatory drugs (NSAIDs), Sombor indices, Quantitative structure-property relationship (QSPR), Pharmacodynamic parameters, Toxicological parameters, Molecular architecture, Physicochemical properties, Drug development, Safety assessment

1. Introduction

Painkillers are widely used to alleviate acute and chronic pain. While acute pain often dissipates when the underlying cause is addressed, chronic pain can persist, leading to prolonged reliance on opioids [1]. However, prolonged or excessive use of opioids can have detrimental effects on health. The human body contains numerous nerves responsible for transmitting messages between body parts, with nerve endings located primarily in the skin, gastrointestinal system, and connective tissues. Painkillers, or analgesics, act through two primary mechanisms: inhibiting the release of prostaglandins to prevent pain signals from reaching the brain, or disrupting communication between nerves to block pain signals [2]. These mechanisms provide temporary relief from pain. Painkillers are broadly categorized into non-prescription (over-the-counter) and prescription medications, with varying efficacy in pain reduction:

  • Nonsteroidal anti-inflammatory drugs (NSAIDs);
  • Non-opioid analgesics;
  • Opioid analgesics;
  • Combination analgesics.

This study focuses on NSAIDs, which, despite their widespread use, may not be suitable for everyone and can sometimes cause adverse effects [3]. NSAID gels and creams applied to the skin may offer localized relief with fewer side effects compared to oral formulations. Chemical graph theory, a branch of mathematical chemistry, deals with chemical graphs that represent molecular structures [4, 5, 6]. Topological indices, a key tool in chemical graph theory, bridge mathematical concepts with chemistry [7, 8, 9]. In this study, we employ topological indices to analyze a variety of pharmaceuticals, developing unique indicators based on node degrees to characterize their chemical properties and processes.

Chemists and pharmacists can utilize graph theory resources for further research, including Quantitative Structure-Activity/Property/Toxicity Relationship (QSAR/QSPR/QSTR) modeling, which predicts biological activity based on molecular structure [10]. Husin et al. provided a topological analysis of certain networks [11]. Recent research has focused on pharmaceutical topological indices and their use in QSAR modeling [12]. Chemical compounds are often represented as vertices on a graph, with edges denoting bonds between them. NSAID drugs under investigation in this study are treated as chemical compounds, and topological indices are defined accordingly. Regression analysis demonstrates a strong correlation between obtained features and NSAID characteristics.

In chemistry, valence and degree in graph theory are related concepts. Quantitative Structure-Property Relationship (QSPR) plays a crucial role in drug design by providing a cost-effective alternative to traditional experimental testing methods [13, 14, 15]. QSAR models are increasingly used in environmental toxicity assessment and drug development to predict toxicity, resistance, and physicochemical properties [13, 14, 15]. In theoretical chemistry, drugs are represented as molecular networks, with edges representing bonds between atoms and vertices representing atoms [13, 14, 15].

Experimental determinations in chemistry can be costly, but QSPR modeling research can help reduce these costs by providing insights into biological processes and structural facets. QSPR and QSAR techniques enable the construction of accurate models predicting the characteristics or actions of organic molecules [16, 17, 18]. However, developing realistic models requires an approach capable of encoding predicted molecular structure descriptors effectively. Descriptor-based modeling allows researchers to pinpoint specific traits influencing the activity or property of interest in compounds [19, 20].

2. Material and Methods

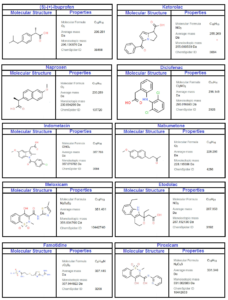
In this study, we employed a rigorous methodology to compute Sombor indices and develop Quantitative Structure-Property Relationship (QSPR) models for the molecular graph of NSAID drugs [3], as illustrated in Figure 1. Initially, we collected a comprehensive dataset of NASID drugs, namely Ketorolac, Diclofenac, Naproxen, Ibuprofen, Meloxicam, Nabumetone, Indomethacin, Famotidine, Etodolac, and Piroxicam, from reliable sources (see Table 1) and meticulously preprocessed the data. Sombor indices were then calculated using established mathematical methods (edge partition technique) and Maple software, yielding a set of descriptors. Subsequently, we partitioned the dataset into distinct training, validation, and test subsets for model development and assessment. QSPR models were constructed employing regression model techniques with defined algorithms and executed using SPSS. Furthermore, external validation on an independent dataset was conducted to ensure the generalizability of the regression models. The interpretation of model findings and statistical analyses were integral parts of our methodology. To enhance reproducibility, the availability of code and data was maintained. This methodology ensures the robustness of our Sombor index-based QSPR modeling for NSAID drugs with properties namely, boiling point (BP), polarity (Pol), complexity (C), refractivity (R), and molecular weight (MW).

Table 1: Different Nsaids and their Physical and Chemical Properties
Drugs Bp Pol C R MW MV
Ketorolac 493.2 26.67 376 70.19 83.1 198.2
Diclofenac 412 27.93 304 75.46 73.1 209.8
Naproxen 403.9 24.81 277 64.85 72.1 195.3
Ibuprofen 157 23.76 203 60.73 62.4 203.3
Meloxicam 581.3 34.25 628 88.62 83.5 220.7
Nabumetone 372.3 26.17 262 68.43 64.3 213.5
Indomethacin 499.4 36.64 506 94.81 83.3 275.6
Famotidine 662.4 31.66 469 80.46 100.3 191.7
Etodolac 507.9 31.66 400 80.46 84.9 248.3
Piroxicam 568.5 32.27 611 87.04 91.3 229.8

3. Sombor Indices and Computational Results

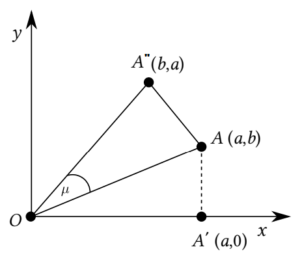
Numerous degree-based graph invariants, also known as “topological indices,” have been presented and thoroughly investigated in the mathematical and chemical literature [19, 20]. Generally, \[\label{e1}\tag{1} TI(G)=\sum_{ij \in E(G)}F(d_i,d_j).\] Here, \(F(x,y)\) represents a function having commutative property, i.e., \(F(x,y)=F(y,x)\).

Sombor and reduced Sombor index [21] are given by \[\label{e2}\tag{2} SO(G)=\sum_{ij{\in}E(G)}\sqrt{d_i^2+d_j^2},\] \[SO_{red}(G)=\sum_{uv{\epsilon}E(G)}\sqrt{(d_{i}-1)^2+(d_{j}-1)^2}.\tag{3}\]

In Eq. (2), the ordered pair \((x, y)\), where \(x = d_i\), \(y = d_j\), \(a \geq b\), known as the degree-coordinate of the edge \(ij \in E(G)\), are expressed by a point degree in a 2D coordinate system, see Figure 2. On the other hand, the dual point degree refers to the coordinates \((b, a)\) pertaining to the edge \(ij\). The distance, assuming Euclidean metrics, between the origin (O) and the degree-point of the edge \(ij\) is \(\sqrt{d_i^2+d_j^2}\) (represented by \(A\) in Figure 2).

Kulli and Gutman presented the modified Sombor index [22], as follows: \[mSO_{red}(G)=\sum_{uv{\epsilon}E(G)}\frac{1}{\sqrt{d_i^2+d_j^2}}.\]

Mendez-Bermudez et al. presented max and min Sombor indices [23]: \[maxSO(G)=\sum_{ij{\epsilon}E(G)}\max(d_i,d_j),\] \[minSO(G)=\sum_{ij{\epsilon}E(G)}\min(d_i,d_j).\]

Wang and Wu in [24] introduced the ideas of exponential and exponential reduced Sombor indices: \[e^{SO(G)}=\sum_{ij{\epsilon}E(G)}e^{\sqrt{d_i^2+d_j^2}},\] \[e^{SO_{red}(G)}=\sum_{ij{\epsilon}E(G)}e^{\sqrt{(d_i-1)^2+(d_j-1)^2}}.\]

Author introduced the idea of the multiplicative version of Sombor indices: \[MSO(G)=\prod_{ij{\epsilon}E(G)}\sqrt{d_i^2+d_j^2},\] \[MSO_{red}(G)=\prod_{ij{\epsilon}E(G)}\sqrt{(d_i-1)^2+(d_j-1)^2}.\]

Theorem 1. Let \(G\) be the graph of Indomethacin. Sombor indices for \(G\) are given as follows:

  • \(SO(G)=95.8923\).
  • \(SO_{red}(G)=59.6384\).
  • \(mSO(G)=7.7898\).
  • \(maxSO(G)=77\).
  • \(minSO(G)=55\).
  • \(e^{SO(G)}=1070.1959\).
  • \(e^{SO_{red}(G)}=273.3562\).
  • \(MSO(G)=235574.7015\).
  • \(MSO_{red}(G)=20661.2691\).

Proof. Let \(G\) be the graph of Indomethacin with edge set \(E\). Let \(E_{m,n}\) be edges in \(G\) such that \(|E_{1,2}|=1\), \(|E_{1,3}|=5\), \(|E_{2,2}|=3\), \(|E_{2,3}|=11\), and \(|E_{3,3}|=7\). By applying the definitions, we obtain the following result: \[\begin{aligned} SO(G)&=\sum_{uv{\in}E(G)}\sqrt{d_u^2+d_v^2}\\ &=(1)\sqrt{1+4}+(5)\sqrt{1+9}+(3)\sqrt{4+4}\\ &\quad+(11)\sqrt{4+9}+(7)\sqrt{9+9}\\ &=95.8923. \end{aligned}\] Similarly, the other indices can be computed. ◻

Theorem 2. Let \(G\) be the graph of Famotidine. Sombor indices for \(G\) are

  • \(SO(G)=70.0920\).
  • \(SO_{red}(G)=43.9437\).
  • \(mSO(G)=5.8103\).
  • \(maxSO(G)=60\).
  • \(minSO(G)=34\).
  • \(e^{SO(G)}=742.5617\).
  • \(e^{SO_{red}(G)}=206.7093\).
  • \(MSO(G)=258486.2172\).
  • \(MSO_{red}(G)=137384.0165\).

Proof. Let \(G\) be the graph of Famotidine with edge set \(E\). Let \(E_{m,n}\) be edges in \(G\) such that \(|E_{1,3}|=3\), \(|E_{1,4}|=4\), \(|E_{2,2}|=4\), \(|E_{2,3}|=9\), and \(|E_{2,4}|=1\). The proof is straightforward by applying the definitions. ◻

Topological indices for other drugs can be computed using similar procedures. Table 2 includes all computed values of NSAID drugs for different versions of Sombor indices. Figures 3 and 4 depict 2D and 3D graphical representations of calculated TIs for various NSAID drugs.

Table 2: Topological Indices of NSAID Drugs
Drugs SO(G) $$SO_red(G)$$ mSO(G) maxSO(G) minSO(G) $$e^SO(G)$$ $$e^SO_red(G)$$ MSO(G) $$MSO_red(G)$$
Ketorolac 73.53 44.87 6.148 57 45 810.74 204.49 88660.04 11591.78
Diclofenac 68.36 41.44 5.95 55 39 682.28 175.73 65674.10 8586.50
Naproxen 62.55 38.43 5.30 51 35 654.05 168.07 49562.47 2897.94
Ibuprofen 48.48 28.61 4.73 27 39 432.42 114.17 16418.53 2146.63
Meloxicam 92.27 58.90 6.96 75 51 1224.87 319.23 7220833.86 495345.12
Nabumetone 56.08 32.85 5.32 45 33 523.10 132.37 7739.77 715.55
Indomethacin 95.89 59.64 7.79 77 55 1070.20 273.36 235574.70 20661.27
Famotidine 70.09 43.94 5.81 60 34 742.56 206.71 258486.22 19440
Etodolac 82.99 53.39 5.26 68 46 1039.67 276.30 2101571.34 137384.02
Piroxicam 73.40 56.67 7.15 72 52 1178.40 271.29 7108008.33 487605.34

4. Regression Model and Structure Analysis

Regression models (RM) are statistical techniques used to analyze and model the relationship between a dependent variable and one or more independent variables. Common types of regression models include linear regression, logistic regression, and polynomial regression, each suited to different types of data and research questions. Here, we will use liner regression model, Eq. (4), to check the relationship between topological indices and the physiochemical features of NSAIDs. \[P=A+b(TI),\tag{4}\] where, \(P\) stands for the NSAID’s characteristic. TI is an independent variable, a and b are regression confident. SPSS is used to find these constants. A linear regression model is used to analyze nine TIs for NSAID and their properties.

4.1. Regression Models for \(SO(G)\)

\[\begin{aligned} BP&=1.480+6.416 [SO(G)],\\ POL&=10.803+0.266 [SO(G)],\\ C&=-156.10+7.734 [SO(G)],\\ R&=29.043+0.660 [SO(G)],\\ MW&=45.776+0.471 [SO(G)],\\ MV&=116.383+1.482 [SO(G)]. \end{aligned}\]

Regression Models for \(SO_{red}(G)\)

\[\begin{aligned} BP&=31.066+9.476[SO_{red}(G)],\\ POL&=13.043+0.361[SO_{red}(G)],\\ C&=-154.500+12.166[SO_{red}(G)],\\ R&=33.736+0.945[SO_{red}(G)],\\ MW&=45.621+0.746[SO_{red}(G)],\\ MV&=143.342+1.641[SO_{red}(G)]. \end{aligned}\]

4.2. Regression Models for \(mSO(G)\)

\[\begin{aligned} BP&=-44.356+84.433[mSO(G)],\\ POL&=7.832+3.5997[mSO(G)],\\ C&=-346.319+124.118[mSO(G)],\\ R&=17.141+9.924[mSO(G)],\\ MW&=41.759+6.301[mSO(G)],\\ MV&=155.129+11.336[mSO(G)]. \end{aligned}\]

4.3. Regression Models for \(maxSO(G)\)

\[\begin{aligned} BP&=76.044+7.5955[maxSO(G)],\\ POL&=14.796+0.207[maxSO(G)],\\ C&=-92.3505+8.4489[maxSO(G)],\\ R&=37.7846+0.6698[maxSO(G)],\\ MW&=46.9939+0.5594[maxSO(G)],\\ MV&=148.4177+1.2811[maxSO(G)]. \end{aligned}\]

4.4. Regression Models for \(minSO(G)\)

\[\begin{aligned} BP&=203.1737+6.1216[minSO(G)],\\ POL&=12.5278+0.3975[minSO(G)],\\ C&=-179.2887+13.5871[minSO(G)],\\ R&=31.3886+1.0657[minSO(G)],\\ MW&=55.7063+0.5623[minSO(G)],\\ MV&=106.4717+2.7307[minSO(G)]. \end{aligned}\]

4.5. Regression Models for \(e^{SO(G)}\)

\[\begin{aligned} BP&=203.1737+6.1216[e^{SO(G)}],\\ POL&=12.5278+0.3975[e^{SO(G)}],\\ C&=-7.1468+0.4914[e^{SO(G)}],\\ R&=47.6308+0.0353[e^{SO(G)}],\\ MW&=56.2138+0.0283[e^{SO(G)}],\\ MV&=162.3887+0.0733[e^{SO(G)}]. \end{aligned}\]

4.6. Regression Models for \(MSO(G)\)

\[\begin{aligned} BP&=428.0.00002187[MSO(G)],\\ POL&=28.28879+0.00000075395[MSO(G)],\\ C&=335.0675+0.00003955[MSO(G)],\\ R&=73.485+0.00000211[MSO(G)],\\ MW&=77.0994+0.000001592[MSO(G)],\\ MV&=215.1036+0.000002050[MSO(G)]. \end{aligned}\]

4.7. Regression Models for \(MSO_{red}(G)\)

\[\begin{aligned} BP&=426.2931+0.00031887[MSO_{red}(G)],\\ POL&=28.27+0.0000111[MSO_{red}(G)],\\ C&=334.7768+0.0005853[MSO_{red}(G)],\\ R&=73.4472+0.000031105[MSO_{red}(G)],\\ MW&=77.10405+0.00002318[MSO_{red}(G)],\\ MV&=215.0691+0.0000302[MSO_{red}(G)]. \end{aligned}\] Tables 3-11 represent different attributes of liner regression model used to determine the correlation coefficient, coefficient of determination and coefficient of variance. Figures 5-58, represents the liner regression between the observed value and exact value for different properties of NSAID.

Table 3: Parameters of RM for \(SO(G)\)
Property N A b r \(r^2\) S
Boiling Point 9 1.480 6.416 0.685 0.469 0.394
Polarity 9 10.803 0.260 0.902 0.814 -1.477
Complexity 9 -156.10 7.734 0.787 0.619 5.652
Refractivity 9 29.043 0.660 0.891 0.794 -1.543
Molecular Weight 9 45.776 0.471 0.595 0.354 0.253
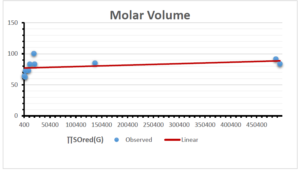
Molecular Volume 9 116.383 1.482 0.621 0.386 -0.643
Table 4: Parameters of RM for \(SO_{red}(G)\)
Property N A b r \(r^2\) S
Boiling Point 9 31.066 9.476 0.740 0.548 -2.760
Polarity 9 13.043 0.361 0.917 0.841 -1.137
Complexity 9 -154.500 12.166 0.905 0.819 -1.043
Refractivity 9 33.736 0.945 0.932 0.869 -1.210
Molecular Weight 9 45.621 0.746 0.690 0.476 0.294
Molecular Volume 9 143.342 1.641 0.680 0.462 -0.800
Table 5: Parameters of RM for \(mSO(G)\)
Property N A b r \(r^2\) S
Boiling Point 9 -44.356 84.433 0.219 0.048 0.439
Polarity 9 7.832 3.600 0.817 0.667 -1.729
Complexity 9 -346.319 124.118 0.823 0.677 -0.706
Refractivity 9 17.141 9.924 0.873 0.762 -1.727
Molecular Weight 9 41.759 6.301 0.520 0.270 0.327
Molecular Volume 9 155.129 11.336 0.310 0.096 0.857
Table 6: Parameters of RM for \(maxSO(G)\)
Property N A b r \(r^2\) S
Boiling Point 9 19.934 7.596 0.834 0.696 0.182
Polarity 9 14.670 0.254 0.908 0.824 -1.160
Complexity 9 -92.351 8.449 0.884 0.781 -1.303
Refractivity 9 37.784 0.670 0.928 0.861 -1.163
Molecular Weight 9 46.994 0.559 0.727 0.552 0.014
Molecular Volume 9 148.418 1.128 0.552 0.305 0.555
Table 7: Parameters of RM for \(minSO(G)\)
Property N A b r \(r^2\) S
Boiling Point 9 203.174 6.122 0.350 0.123 1.234
Polarity 9 12.528 0.398 0.740 0.548 -1.454
Complexity 9 -179.289 13.587 0.740 0.548 -1.726
Refractivity 9 31.389 1.066 0.753 0.567 -1.452
Molecular Weight 9 55.706 0.563 0.381 0.145 1.212
Molecular Volume 9 106.4717 2.731 0.613 0.376 -0.313
Table 8: Parameters of RM for \(e^{SO(G)}\)
Property N A b r \(r^2\) S
Boiling Point 9 203.174 6.122 0.717 0.514 0.595
Polarity 9 12.528 0.398 0.859 0.738 -0.778
Complexity 9 -7.147 0.491 0.924 0.854 -1.197
Refractivity 9 47.631 0.035 0.879 0.773 -0.777
Molecular Weight 9 56.214 0.028 0.661 0.437 0.457
Molecular Volume 9 162.389 0.073 0.568 0.323 -0.691
Table 9: Parameters of RM for \(e^{SO_{red}(G)}\)
Property N A b r \(r^2\) S
Boiling Point 9 138.618 1.528 0.759 0.576 0.3555
Polarity 9 17.638 0.056 0.820 0.672 -0.796
Complexity 9 -15.250 1.956 0.902 0.814 -1.369
Refractivity 9 46.328 0.144 0,822 0.676 -0.799
Molecular Weight 9 54.372 0.119 0.695 0.483 0.219
Molecular Volume 9 157.782 0.307 0.523 0.274 -0.867
Table 10: Parameters of RM for \(MSO(G)\)
Property N A b r \(r^2\) S
Boiling Point 9 428.280 0.00003 0.458 0.235 0.565
Polarity 9 28.289 0.0000008 0.515 0.265 0.537
Complexity 9 335.068 0.00004 0.798 0.637 -1.459
Refractivity 9 73.485 0.000002 0.558 0.311 0.683
Molecular Weight 9 77.099 0.000002 0.395 0.156 0.518
Molecular Volume 9 215.104 0.0000002 0.189 0.036 -0.102
Table 11: Parameters of RM for \(MSO_{red}(G)\)
Property N A b r \(r^2\) S
Boiling Point 9 426.293 0.0003 0.460 0.212 0.612
Polarity 9 28.27 0.00001 0.517 0.267 0.565
Complexity 9 334.777 0.0006 0.801 0.642 -1.498
Refractivity 9 73.447 0.00003 0.562 0.316 0.568
Molecular Weight 9 77.104 0.00002 0.397 0.158 0.561
Molecular Volume 9 215.069 0.00003 0.182 0.033 -0.073

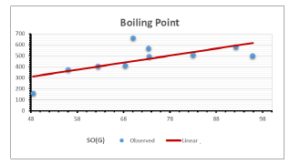
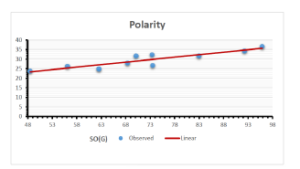
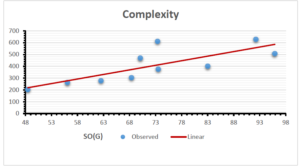
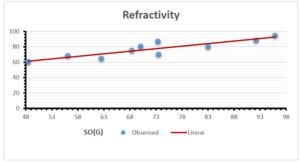
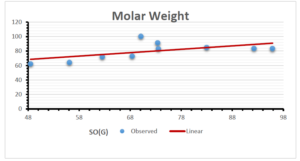
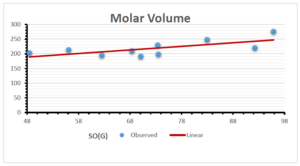
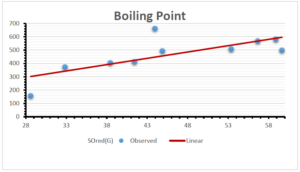
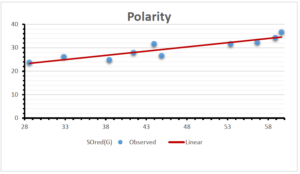
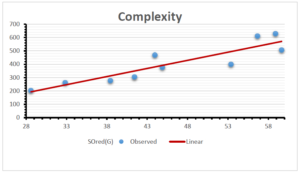
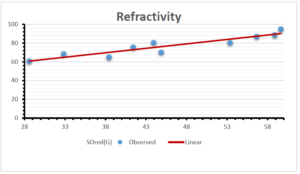
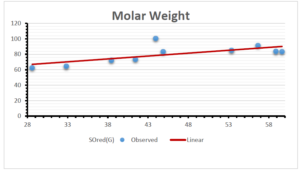
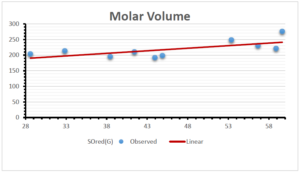
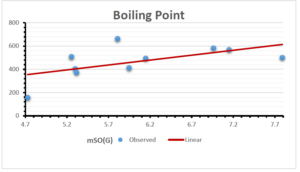
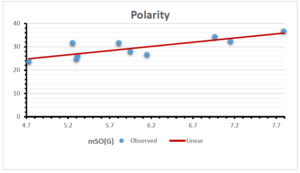
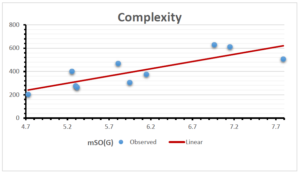
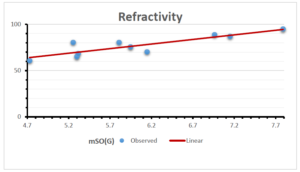
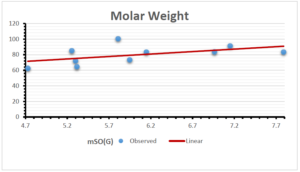
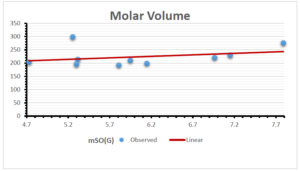
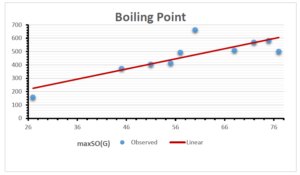
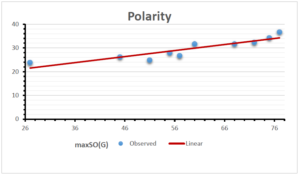
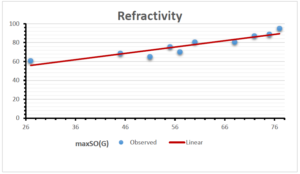
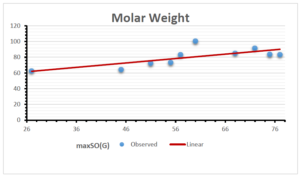
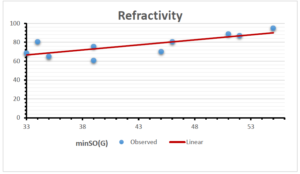
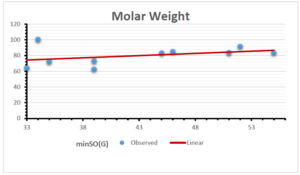
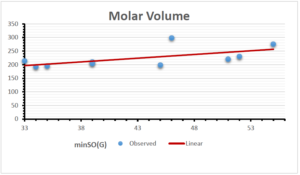
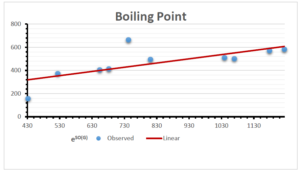
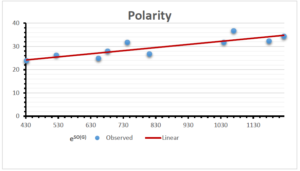
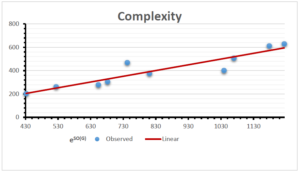
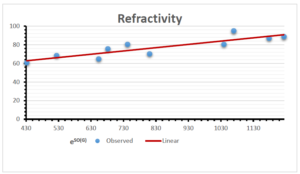
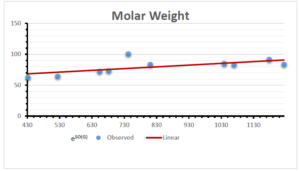
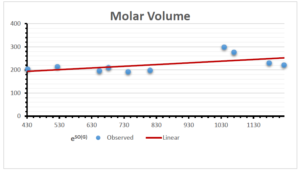
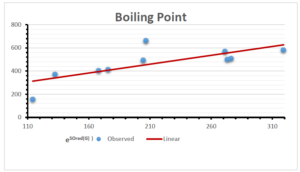
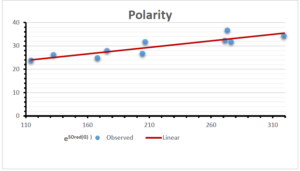
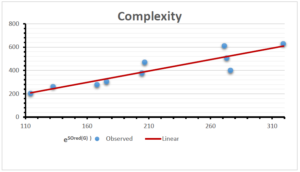
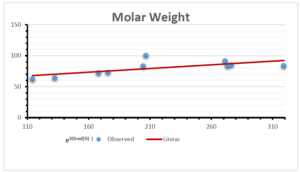
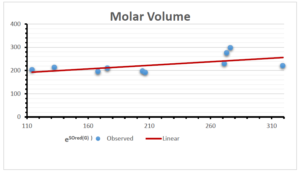
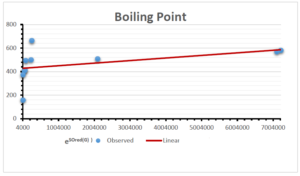
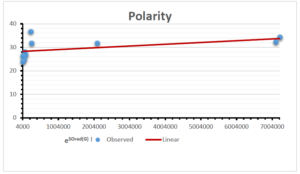
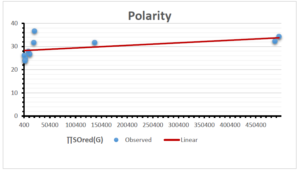
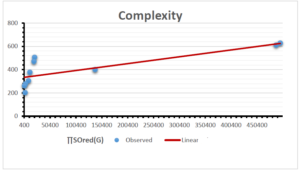
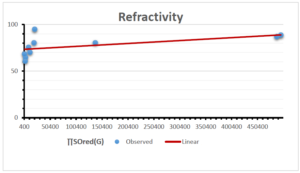
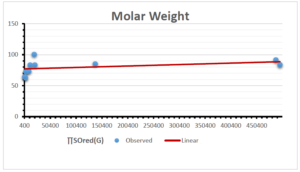
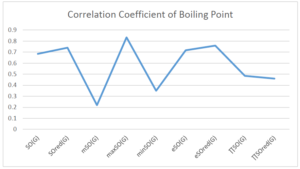
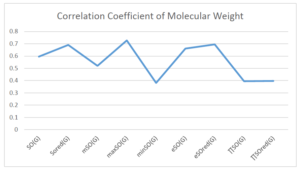
5. Correlation Coefficients of Sombor Indices with Properties of NSAIDS Drugs

The correlation coefficient plays a pivotal role in the analysis of the relationship between the properties of NSAID and their linear regression models. These coefficients are not only valuable for characterizing these relationships but also for building predictive linear regression models. Gutman, gives the capacitative text by which we can check the validity of an index. According to Gutman, an index with specific property of a drug in useful, if its correlation coefficient is greater then 0.8, otherwise index is useless for us [25]. Table 14 represents the Correlation Coefficients of Sombor indices with Properties of NSAIDS in tabular form and Figures 59–64 represents graphical representation. , Table 12 and 13, represents the coefficient determination and coefficient of variance, respectively.

Table 12: Coefficient of Determination
Topological Index Bp Pol C R MW MV
\(SO(G)\) 0.469 0.814 0.619 0.794 0.354 0.386
\(SO_{red}(G)\) 0.548 0.841 0.819 0.819 0.476 0.462
\(mSO(G)\) 0.048 0.667 0.677 0.762 0.270 0.096
\(maxSO(G)\) 0.696 0.824 0.781 0.861 0.552 0.305
\(minSO(G)\) 0.123 0.548 0.548 0.567 0.145 0.376
\(e^{SO(G)}\) 0.514 0.0.738 0.854 0.773 0.437 0.323
\(e^{SO_{red}(G)}\) 0.576 0.672 0.814 0.676 0.483 0.274
\(MSO(G)\) 0.235 0.265 0.647 0.311 0.156 0.036
\(MSO_{red(G)}\) 0.267 0.517 0.646 0.316 0.158 0.033
Table 13: Coefficient of Vaiance
Topological Index Bp Pol C R MW MV
\(SO(G)\) 19.632 19.632 19.632 19.632 19.632 19.632
\(SO_{red}(G)\) 22.652 22.652 22.652 22.652 22.652 22.652
\(mSO(G)\) 15.252 15.252 15.252 15.252 15.252 15.252
\(maxSO(G)\) 24.887 24.887 24.887 24.887 24.887 24.887
\(minSO(G)\) 17.736 17.736 17.736 17.736 17.736 17.736
\(e^{SO(G)}\) 31.450 31.450 31.450 31.450 31.450 31.450
\(e^{SO_{red}(G)}\) 30.298 30.298 30.298 30.298 30.298 30.298
\(MSO(G)\) 162.592 162.592 162.592 162.592 162.592 162.592
\(MSO_{red}(G)\) 160.429 160.429 160.429 160.429 160.429 160.429
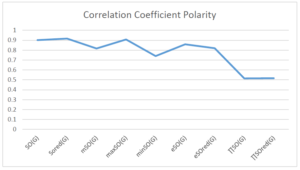
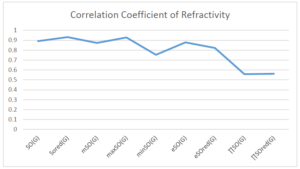
Table 14: Tabular Representation of Correlation Coefficients of Sombor Indices with Properties of NSAIDS Drugs
Topological Index Bp Pol C R MW MV
\(SO(G)\) 0.685 0.902 0.787 0.891 0.595 0.621
\(SO_{red}(G)\) 0.740 0.917 0.905 0.932 0.690 0.680
\(mSO(G)\) 0.219 0.817 0.832 0.873 0.520 0.310
\(maxSO(G)\) 0.834 0.908 0.884 0.928 0.727 0.552
\(minSO(G)\) 0.350 0.740 0.740 0.753 0.381 0.613
\(e^{SO(G)}\) 0.717 0.859 0.924 0.879 0.661 0.568
\(e^{SO_{red}(G)}\) 0.759 0.820 0.902 0.822 0.695 0.523
\(MSO(G)\) 0.458 0.515 0.798 0.558 0.395 0.189
\(MSO_{red}(G)\) 0.460 0.517 0.801 0.562 0.397 0.182

6. Conclusion

A structure can be given a single number by employing the topological index. Knowledge of topological indices plays a key role in the link between quantitative structure activity as well as property. our study has provided valuable insights into the relationships between the physical properties of NSAIDs and different versions of Sombor indices, shedding light on the intricate interplay between these factors. By calculating and analyzing the correlation coefficients, we have discerned the strength and direction of associations between specific drug properties and the derived topological indices. These findings are instrumental in understanding how drug physicochemical characteristics influence molecular structure and, consequently, their behavior within biological systems. The results not only contribute to the field of pharmaceutical research but also offer practical implications for drug design, optimization, and prediction of pharmacological outcomes. According to Gutman [25], indices with correlation coefficient greater then 0.8 in useful. Table 14, shows significant results in testing Sombor indices and their implementation on diffident properties of NSAIDs. Sombor and its reduced version gives best result with polarity of NSAIDs drugs. While, exponential Sombor indices are best for predicting the complexity of NSAIDs. Reduce Sombor index is good to predict the value of refractivity for NSAIDs. Further research can build upon these findings to refine drug development strategies and enhance the pharmaceutical industry’s ability to deliver safer and more effective therapeutic agents.

Conflict of Interest

The authors declare no conflict of interest.

References:

  1. Huang, R., Mahboob, A., Rasheed, M. W., Alam, S. M. and Siddiqui, M. K., 2023. On molecular modeling and QSPR analysis of lyme disease medicines via topological indices. The European Physical Journal Plus, 138(3), p.243.
  2. Réti, T., Sharafdini, R., Dregelyi-Kiss, A. and Haghbin, H., 2018. Graph irregularity indices used as molecular descriptors in QSPR studies. MATCH Commun. Math. Comput. Chem, 79, pp.509-524.
  3. Gnanaraj, L. R. M., Ganesan, D. and Siddiqui, M. K., 2023. Topological indices and QSPR analysis of NSAID drugs. Polycyclic Aromatic Compounds, pp.1-17.
  4. Ajmal, M., Nazeer, W., Munir, M., Kang, S. M. and Jung, C. Y., 2017. The M-polynomials and topological indices of generalized prism network. International Journal of Mathematical Analysis, 11(6), pp.293-303.
  5. Shao, Z., Virk, A. R., Javed, M. S., Rehman, M. A. and Farahani, M. R., 2019. Degree based graph invariants for the molecular graph of Bismuth Tri-Iodide, Eng. Appl. Sci. Lett.,2(1), pp.01-11.
  6. Wiener, H., 1947. Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69 (1), pp.17-20.
  7. Virk, A. R., Jhangeer, M. N. and Rehman, M. A., 2018. Reverse Zagreb and reverse hyper-Zagreb indices for silicon carbide \(Si_{2}C_{3}-I[r,s]\) and \(Si_{2}C_{3}-II[r,s]\). Eng. Appl. Sci. Lett.,1(2), pp.37-48.
  8. Gutman, I. and Polansky, O. E., 2012. Mathematical concepts in organic chemistry. Springer Science & Business Media.
  9. Randić, M., 1975. Characterization of molecular branching. Journal of the American Chemical Society, 97 (23), pp.6609-6615.
  10. Randić, M., 1993. Comparative regression analysis. Regressions based on a single descriptor. Croatica Chemica Acta, 66(2), pp.289-312.
  11. Husin, M. N., Zafar, S. and Gobithaasan, R. U., 2022. Investigation of atom-bond connectivity indices of line graphs using subdivision approach. Mathematical Problems in Engineering, 2022, pp.1-9.
  12. Randić, M., 1996. Quantitative structure-property relationship. Boiling points of planar benzenoids. New Journal of Chemistry, 20(10), pp.1001-1009.
  13. Amin, S., Rehman Virk, A.U., Rehman, M.A. and Shah, N.A., 2021. Analysis of dendrimer generation by Sombor indices. Journal of Chemistry, 2021, pp.1-11.
  14. Caporossi, G., Gutman, I., Hansen, P. and Pavlovic, L., 2003. Graphs with maximum connectivity index. Computational Biology and Chemistry, 27(1), pp.85-90.
  15. Gutman, I., 2018. Topological indices and irregularity measures. J. Bull, 8, pp.469-475.
  16. Li, X. and Shi, Y., 2008. A survey on the Randić index. MATCH Commun. Math. Comput. Chem, 59(1), pp.127-156.
  17. Huo, C. G., Azhar, F., Virk, A. U. R. and Ismaeel, T., 2022. Investigation of Dendrimer Structures by Means of K-Banhatti Invariants. Journal of Mathematics, 2022, p.4451899.
  18. Gutman, I. and Das, K. C., 2004. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem, 50(1), pp.83-92.
  19. Wiener, H., 1947. Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69 (1), pp.17-20.
  20. Randić, M., 1975. Characterization of molecular branching. Journal of the American Chemical Society, 97 (23), pp.6609-6615.
  21. Gutman, I., 2021. Geometric approach to degree-based topological indices: Sombor indices. MATCH Commun. Math. Comput. Chem, 86(1), pp.11-16.
  22. Kulli, V. R. and Gutman, I., 2021. Computation of Sombor indices of certain networks. International Journal of Applied Chemistry, 8(1), pp.1-5.
  23. Méndez-Bermúdez, J. A., Aguilar-Sánchez, R., Molina, E. D. and Rodríguez, J. M., 2021. Mean Sombor index. Discrete Math. Lett, 9, pp.18-25.
  24. Wang, F. and Wu, B., 2022. The reduced Sombor index and the exponential reduced Sombor index of a molecular tree. Journal of Mathematical Analysis and Applications, 515(2), p.126442.
  25. Gutman, I., 2013. Degree-based topological indices. Croatica Chemica Acta, 86(4), p.351-361.
Information
Guidelines
CP Initiatives
Follow CP
Facebook X-twitter Linkedin
1970-2024 CP (Manitoba, Canada) unless otherwise stated.
Citation
Abaid ur Rehman Virk, Muhammad Usman. Decoding Nonsteroidal Anti-inflammatory Drugs with Sombor Invariants: A Quantum Leap in QSPR Modeling[J], Utilitas Mathematica, Volume 119. 83-116. DOI: https://doi.org/10.61091/um119-09.