Contents

  1. 1. Introduction
  2. 2. Discussion and Results
  3. 3. Conclusion
  4. Conflict of Interest

Utilitas Mathematica

  • Research article

On Exploring the Topological Aspects of the Chemical Structure of the Nanotube HAC5C7[w,t]

Muhammad Saqlain Zakir1, Muhammad Kamran Naseer2, Muhammad Reza Farahani3, Irfan Ahmad2, Zarqa Kanwal2, Mehdi Alaeiyan3, Murat Cancan4
1Department of Mathematics, COMSATS University Islamabad, Sahiwal Campus, Sahiwal, 57000, Pakistan
2Department of Mathematics, Lahore Leads University, Lahore, Pakistan
3Department of Mathematics and Computer Science, In University of Science and Technology (IUST), Narmak, Tehran, 16844, Iran
4Faculty of Education, Van Yuzuncu Yıl University, Zeve Campus, Tuşba, 65080, Van, Turkey
  • Received: 10/09/2023
  • Accepted: 20/12/2023
  • Published: 31/03/2024

Abstract

Graph theory has experienced notable growth due to its foundational role in applied mathematics and computer science, influencing fields like combinatorial optimization, biochemistry, physics, electrical engineering (particularly in communication networks and coding theory), and operational research (with scheduling applications). This paper focuses on computing topological properties, especially in molecular structures, with a specific emphasis on the nanotube HAC5C7[w,t].

Keywords: Graph theory, Topological indices, Molecular structures, Nanotubes, Computational chemistry

1. Introduction

Graph theory originated with Leonhard Euler’s solution to the Seven Bridges of Königsberg problem in 1735. It has since become a fundamental area of applied mathematics, dealing with the study of objects with connections and points known as graphs. If these connections are all one-way, the graph is termed a directed graph or digraph. Graph theory finds applications in various fields such as computer science, where it is used to model communication networks, computational devices, data organization, and computation flow. Additionally, it is employed to study molecular properties in chemistry, physics, and biology.

Claude Shannon’s seminal work laid the groundwork for exploring the information content of graphs and networks over the past half-century [1, 2]. Graph entropy has emerged as a metric to measure the structural complexity of graphs and networks [3], with applications in disciplines like information theory, biology, chemistry, and sociology.

In mathematics, graph theory entails the study of graphs, which are represented by vertices (nodes) connected by edges (lines). These mathematical structures are utilized to examine pairwise relations between objects, facilitating the construction of road maps, diagrams, and other schematics. Graphs play a crucial role in modern technological processes and communication, fostering logical and abstract thinking. For instance, connecting dots to form shapes like animals in a game represents a basic form of graph.

Chemical graph theory, a branch with around 500 articles published annually, focuses on chemical indices derived from graph theory. These indices find applications in chemistry, aiding chemists in their analyses. Prominent indices include the Zagreb indices, Wiener index, Randic index, and various connectivity indices [4, 5, 6, 7]. Topological indices, defined as graph invariants useful for chemical determinations, play a significant role in quantitative structure-property and structure-activity relationships (QSPR and QSAR) [8, 9, 10, 11, 12, 13, 14, 15].

The study of graphs extends to their relationship with finite sequences of symbols, as seen in Parikh word representable graphs (PWRGs). PWRGs are introduced based on the concept of subwords and the Parikh matrix, leading to investigations into their properties [16, 17, 18, 19, 20, 21, 22].

Furthermore, chemical graph theory has sparked interest in various topological indices associated with graphs, aiming to describe molecular structures in terms of these indices [23, 24, 25, 26, 27, 28, 29]. Numerous studies have provided formulas for computing these indices and established constraints on their values [30, 31].

This paper focuses on distance-based topological indices of binary core word PWRGs, expanding upon recent research in the field.

Topological indices are real numbers associated with compounds and graph networks, providing insights into their properties. These indices remain invariant and are crucial for predicting the properties and bioactivity of compounds in cheminformatics. They establish quantitative relationships between molecular structure and property/activity. Polynomials, such as the Wiener polynomial or Hosoya polynomial [32], are instrumental in creating distance-dependent topological indices. The M-polynomial, introduced earlier, is used for degree-dependent topological indices, reflecting the close relationship between valence and degree in chemistry [33].

Since the 1970s, degree-based graph invariants like the First and Second Zagreb indices have been widely studied. Various types of graph indices are discussed below.

Definition 1. The first (a,b)-KA index, denoted KA(a,b)1(G), is defined as (1)KA(a,b)1(G)=∑xy∈E(G)[(dG(x)a+dG(y)a)]b, where a,b∈R are suitably chosen parameters.

Definition 2. The reduced 1st (a,b)-KA index for a graph G is defined as (2)RKAa,b1(G)=∑xy∈E(G)[(dG(x)−1)a+(dG(y)−1)a].

Definition 3. The reduced 2nd (a,b)-KA index for a graph G is defined as (3)RKAa,b2(G)=∑xy∈E(G)[(dG(x))a(dG(y))a].

Definition 4. The reduced 2nd (a,b)-KA index for a graph G is defined as (4)RKAa,b2(G)=∑xy∈E(G)[(dG(x)−1)a(dG(y)−1)a].

Definition 5. The Sombor index is introduced in [34] as (5)SO(G)=∑xy∈E(G)(dG(x)2+(dG(y))2). If we set a=2 and b=12 in the first (a,b)-KA index, we obtain the Sombor index.

Definition 6. The modified Sombor index, denoted by mSO(G) [35], for a graph G is defined as (6)mSO(G)=∑xy∈E(G)1(dG(x)2+(dG(y)2).

Definition 7. The reduced Sombor index for a graph G can be defined as (7)RSO(G)=∑xy∈E(G)(dG(x−1)2+(dG(y−1)2).

Definition 8. The reduced modified Sombor index for a graph G can be defined as (8)RSO(G)=∑xy∈E(G)1(dG(x−1)2+(dG(y−1)2).

2. Discussion and Results

In this section, we delve into the chemical structures of the nanotubes, specifically HAC5C7[w,t]. By employing the edge partition of the nanotube, we evaluate several topological invariants.

2.1. Topological Indices of HAC5C7[w;t] Nanotube

Figure 1 displays the carbon nanotube HAC5C7[w;t]’s molecular graphs. Cycles C5 and C7(C5C7) net, a trivalent decoration made by alternating C5 and C7 by various chemicals, make up the architecture of this nanotube. It can cover a torus or a cylinder.

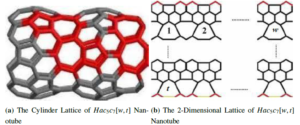
Heptagon and pentagon nets make up the structure of this nanotube. Since all C5C7 nets are 8 bytes in size and there are wt heptagons C7 in H, the size of the vertex set of the HAC5C7[w;t] nanotube (w,t) is equal to n=V(HAC5C7[w;t])=8wt+2w. On the other hand, the first row of H has w numbers of vertices with degree 2, while the last row of H contains w numbers of vertices.

Figure 1 shows that the edge set of HAC5C7[w,t] may be classified into the following groups: E1={jk∈E(HAC5C7[w,t]):dj=2;dk=2},E2={jk∈E(HAC5C7[w,t]):dj=3;dk=2},E3={jk∈E(HAC5C7[w,t]):dj=3;dk=3}. Such that |E1|=0;|E2|=4w;|E3|=12wt−2w. We may immediately obtain the findings listed below from this edge partition.

Theorem 1. The KA(a,b)1 of HAC5C7[w,t] is KA(a,b)1(HAC5C7[w,t])=αw+βwt, where α=2[2(3a+2a)b−(2×3a)b] and β=12[(2×3a)b].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] that is shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t] and by using the Eq. (1), KA(a,b)1(HAC5C7[w,t])=|E1|[2a+2a]b+|E2|[3a+2a]b+|E3|[3a+3a]b=0[2(a+1)]b+4w[3a+2a]b+(12wt−2w)[2×3a]b=2[2(3a+2a)b−(2×3a)b]w+12[(2×3a)b]wt=αw+βwt, where α=2[2(3a+2a)b−(2×3a)b] and β=12[(2×3a)b]. ◻

Theorem 2. The RKA(a,b)1 of HAC5C7[w,t] is RKA(a,b)1(HAC5C7[w,t])=αw+βwt, where α=2[2(1+2a)b−2(ab+b)] and β=3[2(ab+b+2)].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] that is shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t], by using Eq. (2), we have RKA(a,b)1(HAC5C7[w,t])=|E1|[(2−1)a+(2−1)a]b+|E2|[(3−1)a+(2−1)a]b+|E3|[(3−1)a+(3−1)a]b=0[2]b+4w[1+2a]b+(12wt−2w)[2(a+1)]b=2[2(1+2a)b−2(ab+b)]w+3[2(ab+b+2)]wt=αw+βwt, where α=2[2(1+2a)b−2(ab+b)] and β=3[2(ab+b+2)]. ◻

Theorem 3. The KA(a,b)2 of HAC5C7[w,t] is KA(a,b)2(HAC5C7[w,t])=αw+βwt, where α=2[2(6)ab−(3)2ab] and β=4[(3)(2ab+1)].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t] and by Eq. (3), we have KA(a,b)2(HAC5C7[w,t])=|E1|[2a×2a]b+|E2|[3a×2a]b+|E3|[3a×3a]b=0[22a]b+4w[6a]b+(12wt−2w)[32a]b=2[2(6)ab−(3)2ab]w+4[(3)(2ab+1)]wt=αw+βwt, where α=2[2(6)ab−(3)2ab] and β=4[(3)(2ab+1)]. ◻

Theorem 4. The RKA(a,b)2 index of HAC5C7[w,t] is RKA(a,b)2(HAC5C7[w,t])=αw+βwt, where, α=2ab+2−22ab+1 and β=3[22(ab+1)].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t] and Eq. (4), we have RKA(a,b)2(HAC5C7[w,t])=|E1|[(2−1)a×(2−1)a]b+|E2|[(3−1)a×(2−1)a]b+|E3|[(3−1)a×(3−1)a]b=0+4w[2a]b+(12wt−2w)[22a]b=αw+βwt, where, α=2ab+2−22ab+1 and β=3[22(ab+1)]. ◻

Theorem 5. The Sombor index of HAC5C7[w,t] is S(HAC5C7[w,t],H2)=αw+βwt, where, α=2[213−32] and β=36[2].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t] and Eq. (5), we have SO(HAC5C7[w,t])=|E1|(22+22)+|E2|(22+32)+|E3|(32+32)=08+4w13+(12wt−2w)18=[413−62]w+36[2]wt=αw+βwt, where, α=2[213−32] and β=36[2]. ◻

Theorem 6. The modified Sombor index of HAC5C7[w,t] is mSO(HAC5C7[w,t],H2)=αw+βwt where, α=413−23 and β=2[2].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t] and Eq. (6), we have mSO(HAC5C7[w,t])=|E1|(22+22)+|E2|(22+32)+|E3|(32+32)=08+4w13+(12wt−2w)18=[413−23]w+2[2]wt=αw+βwt, where, α=413−23 and β=2[2]. ◻

Theorem 7. The reduced Sombor index of HAC5C7[w,t] is RSO(HAC5C7[w,t],H2)=αw+βwt, where, α=4[5−2] and β=24[2].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t] and Eq. (7), we have RSO(HAC5C7[w,t])=|E1|(2−1)2+(2−1)2+|E2|(2−1)2+(3−1)2+|E3|(3−1)2+(3−1)2=02+4w5+(12wt−2w)8=4[5−2]w+24[2]wt=αw+βwt, where, α=4[5−2] and β=24[2]. ◻

Theorem 8. The modified reduced Sombor index of HAC5C7[w,t] is mRSO(HAC5C7[w,t],H2)=αw+βwt, where, α=45−112 and β=3[2].

Proof. Consider a chemical structure of nanotube HAC5C7[w,t] shown in Figure 1, using the edge partition of nanotube HAC5C7[w,t] and Eq. (8), we have mRSO(HAC5C7[w,t])=|E1|(2−1)2+(2−1)2+|E2|(2−1)2+(3−1)2+|E3|(3−1)2+(3−1)2=02+4w5+(12wt−2w)8=[45−112]w+3[2]wt=αw+βwt, where, α=45−112 and β=3[2]. ◻

3. Conclusion

In the realm of molecular studies, topological indices have emerged as indispensable tools, offering valuable numerical descriptors that encapsulate the nuances of various molecular structures. Through our in-depth exploration, we’ve calculated numerous topological properties, including, but not limited to, the 1st KA index, reduced 1st KA index, the 2nd KA index, and the reduced 2nd KA index, the Sombor index, modified Sombor index, reduced Sombor index, and modified reduced Sombor index, focusing specifically on the nanotube HAC5C7[w,t]. A notable outcome of our research is the observation that the culmination of each theorem invariably takes a quadratic form, highlighting a consistent pattern in our findings. Moreover, the graphical representations and comparisons significantly enhanced our comprehension of these indices. Not only did these visuals serve as clarifying agents, but they also underscored the potency of the indices in delivering outstanding results. As we forge ahead in this field, the insights gained from this study reaffirm the invaluable role of topological indices in understanding molecular intricacies.

Conflict of Interest

The authors declare no conflict of interest.

References:

  1. Cole, C., 1993. Shannon revisited: Information in terms of uncertainty. Journal of the American Society for Information Science, 44(4), pp.204-211.
  2. Trucco, E., 1956. A note on the information content of graphs. The Bulletin of Mathematical Biophysics, 18, pp.129-135.
  3. Ji, S., Li, X. and Huo, B., 2014. On reformulated Zagreb indices with respect to acyclic, unicyclic and bicyclic graphs. MATCH Commun. Math. Comput. Chem, 72(3), pp.723-732.
  4. Araujo, O. and De La Pena, J.A., 1998. The connectivity index of a weighted graph. Linear Algebra and Its Applications, 283(1-3), pp.171-177.
  5. Gutman, I. and Trinajstić, N., 1972. Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17(4), pp.535-538.
  6. Randic, M., 1975. Characterization of molecular branching. Journal of the American Chemical Society, 97(23), pp.6609-6615.
  7. Tomescu, I., Arshad, M. and Jamil, M. K., 2015. Extremal topological indices for graphs of given connectivity. Filomat, 29(7), pp.1639-1643.
  8. Garca-Domenech, R., Glvez, J., de Julin-Ortiz, J. V. and Pogliani, L., 2008. Some new trends in chemical graph theory. Chemical Reviews, 108(3), pp.1127-1169.
  9. Bozkurt, S. B., Gngr, A. D., Gutman, I. and Cevik, A. S., 2010. Randic matrix and Randic energy. MATCH Commun. Math. Comput. Chem, 64(1), pp.239-250.
  10. Kier, L.B. and Hall, L.H., 1986. Molecular Connectivity in Structure-Activity Analysis. John Wiley & Sons, New York.
  11. Pogliani, L., 2000. From molecular connectivity indices to semi-empirical connectivity terms: Recent trends in graph-theoretical descriptors. Chemical Reviews, 100(10), pp.3827-3858.
  12. Saqlain Zakir, M., Arshad, M., Naseer, M. and Cancan, M., 2023. One Study of Weighted Entropy Based on Topological Indices for Triazine-Based Dendrimer: A Mathematical Chemistry Approach, European Chemical Bulletin, 12, pp. 3630-3645.
  13. Todeschini, R. and Consonni, V., 2008. Handbook of Molecular Descriptors (Vol. 11). John Wiley and Sons.
  14. Jana, C., Jayamurugan, G., Ganapathy, R., Maiti, P. K., Jayaraman, N. and Sood, A. K., 2006. Structure of poly (propyl ether imine) dendrimer from fully atomistic molecular dynamics simulation and by small angle x-ray scattering. The Journal of Chemical Physics, 124(20), pp.204719-204719.
  15. Yunzhu, L., Lingling, W. and Qingrong, Q., 2015. Synthesis of novel peptide dendrimers PDL-GB2 and PDL-G2. The Scientific World Journal, 2015, p.907859.
  16. Atanasiu, A., 2007. Binary amiable words. International Journal of Foundations of Computer Science, 18(02), pp.387-400.
  17. Atanasiu, A., Atanasiu, R. and Petre, I., 2008. Parikh matrices and amiable words. Theoretical Computer Science, 390(1), pp.102-109.
  18. Bera, S., Mahalingam, K. and Subramanian, K.G., 2018. Properties of Parikh matrices of binary words obtained by an extension of a restricted shuffle operator. International Journal of Foundations of Computer Science, 29(03), pp.403-413.
  19. Mateescu, A. and Salomaa, A., 2004. Matrix indicators for subword occurrences and ambiguity. International Journal of Foundations of Computer Science, 15(02), pp.277-292.
  20. Subramanian, K.G., Huey, A.M. and Nagar, A.K., 2009. On Parikh matrices. International Journal of Foundations of Computer Science, 20(02), pp.211-219.
  21. Teh, W.C., 2015. On core words and the Parikh matrix mapping. International Journal of Foundations of Computer Science, 26(01), pp.123-142.
  22. Teh, W.C. and Kwa, K.H., 2015. Core words and Parikh matrices. Theoretical Computer Science, 582, pp.60-69.
  23. Bera, S. and Mahalingam, K., 2016. Structural properties of word representable graphs. Mathematics in Computer Science, 10, pp.209-222.
  24. Mathew, L., Thomas, N., Bera, S. and Subramanian, K.G., 2019. Some results on Parikh word representable graphs and partitions. Advances in Applied Mathematics, 107, pp.102-115.
  25. Aslam, A., Luis Garcıa Guirao, J., Ahmad, S. and Gao, W., 2017. Topological indices of the line graph of subdivision graph of complete bipartite graphs. Applied Mathematics & Information Sciences, 11(6), pp.1631-1636.
  26. Gao, W., Iqbal, Z., Ishaq, M., Sarfraz, R., Aamir, M. and Aslam, A., 2018. On eccentricity-based topological indices study of a class of porphyrin-cored dendrimers. Biomolecules, 8(3), p.71.
  27. Gao, W., Iqbal, Z., Ishaq, M., Aslam, A. and Sarfraz, R., 2019. Topological aspects of dendrimers via distance based descriptors. IEEE access, 7, pp.35619-35630.
  28. Kang, S.M., Iqbal, Z., Ishaq, M., Sarfraz, R., Aslam, A. and Nazeer, W., 2018. On eccentricity-based topological indices and polynomials of phosphorus-containing dendrimers. Symmetry, 10(7), p.237.
  29. Diudea, M.V., 2017. Multi-Shell Polyhedral Clusters (Vol. 10). Springer.
  30. Gutman, I. and Polansky, O.E., 2012. Mathematical concepts in organic chemistry. Springer Science & Business Media.
  31. Thomas, N., Mathew, L., Sriram, S. and Subramanian, K.G., 2021. Wiener-type indices of Parikh word representable graphs. Ars Mathematica Contemporanea, (2), pp.243-260.
  32. Gutman I., 1993. Some properties of the Wiener polynomials, Graph Theory, Notes New York, 125, p.1318.
  33. Munir, M., Nazeer, W., Shahzadi, Z. and Kang, S.M., 2016. Some invariants of circulant graphs. Symmetry, 8(11), p.134.
  34. Gutman, I., 2021. A geometric approach to degree-based topological indices: Sombor indices. Match Commun. Math. Comput. Chem, 86(1), pp.11-16.
  35. Kulli, V. R. and Gutman, I., 2021. Computation of Sombor indices of certain networks. SSRG International Journal of Applied Chemistry, 8(1), pp.1-6.
Information
Guidelines
CP Initiatives
Follow CP
Facebook X-twitter Linkedin

1970-2025 CP (Manitoba, Canada) unless otherwise stated.