Menu
This paper presents an investigation of a modified Leslie-Gower predator-prey model that incorporates fractional discrete-time Michaelis-Menten type prey harvesting. The analysis focuses on the topology of nonnegative interior fixed points, including their existence and stability dynamics. We derive conditions for the occurrence of flip and Neimark-Sacker bifurcations using the center manifold theorem and bifurcation theory. Numerical simulations, conducted with a computer package, are presented to demonstrate the consistency of the theoretical findings. Overall, our study sheds light on the complex dynamics that arise in this model and highlights the importance of considering fractional calculus in predator-prey systems with harvesting.
Predation is a crucial interaction that occurs between various species in nature, enabling the existence of most species in our ecosystem and supporting the rich biodiversity of complex ecosystems [1]. Mathematical models and their dynamics provide an apt explanation for the complexities arising from predator-prey relationships. These models also offer methods to optimally manage renewable resources and establish coexistence conditions for predators and prey [2]. The most fundamental model proposed for this ecosystem was the Lotka-Volterra model, introduced in the early 20th century [3,4]. While this model captured the oscillating behavior in populations of predators and their prey, its simplicity is unable to address most real-world scenarios, leading researchers to propose many modifications of the Lotka-Volterra type model [5].
An alternative to the Lotka-Volterra model is the Leslie model proposed by Leslie [6]. This model suggests that the number of prey and the carrying capacity of the predator’s environment are proportional, a factor not included in the Lotka-Volterra model. Leslie’s model addresses the issue of unbounded growth in both predator and prey populations, and it has been shown to possess globally asymptotically stable and unique positive equilibrium for any permissible parameters [7]. The model’s stability with Holling functional responses was later shown by May [8], and global stability of the unique interior equilibrium was proved for a Leslie-Gower predator-prey model with feedback controls by Chen et al. [9]. The uniqueness of limit cycles and Hopf bifurcation for this model were also discussed in [10,11].
While predator-prey models are widely used to understand complex interactions between different species in an ecosystem, the primary limitation of the Leslie-Gower predator-prey model is that the predator cannot switch to alternative food sources if the prey population is at low densities [12]. To address this limitation, Aziz-Alaoui and Daher [13] introduced a provisional alternative food source parameter, leading to the modified Leslie-Gower predator-prey model. This model has been utilized in various applications, such as modeling the biological control of the prickly-pear cactus by the moth Cactoblastis cactorum [14] and predator-prey mite outbreak interactions on fruit trees [15,16]. For further details on the modified Leslie-Gower model and its applications, see [17,18] and the references therein. Additionally, the Allee effect, introduced by W.C. Allee in [19], has been incorporated into the Leslie-Gower type models, and the stability dynamics and bifurcation analysis of predator-prey systems subject to Allee effects are discussed in [20-23].
Harvesting biological species is a necessary practice for economic development and resource utilization. However, human population growth and natural resource exploitation have resulted in ecological imbalances and species extinction. Although harvesting can minimize damage, it can also lead to predator species extinction [24]. Therefore, it is essential to reinforce scientific management of harvesting practices. Clark [2] discussed the problem of non-selective harvesting of two ecologically independent populations with the logistic growth law. Multi-species harvesting models have been studied in detail by Chaudhuri [25,26], Mesterton-Gibbons [27], and Kar and Chaudhuri [28,29]. Non-selective harvesting models of prey-predator fisheries have also been studied in detail by Chaudhuri and Ray [30] and Kar et al., [31]. Scientific management of harvesting practices can help minimize the impact on predator-prey dynamics and promote ecological stability.
The Michaelis-Menten-type predator-prey model proposes that the per capita growth rate of predators is directly affected by the ratio of prey to predator abundance. Experimental and observational data support this model’s effectiveness, particularly for predators that must compete for prey. For further details, see [32]-[33]. This model has been extensively studied ([34]-[35]), revealing rich dynamics such as stable limit cycles, multiple attractors, and deterministic extinction. Various parametric values result in the existence of hyperbolic, parabolic, and elliptic orbits near the origin and combinations of such orbits.
Continuous predator-prey models have been extensively used to study the interactions between two species. However, these models have some limitations. Specifically, they assume that the subject species have continuous and overlapping generations, which is not always the case. For instance, salmon have an annual spawning season and are born at the same time each year. In such cases, discrete-time models are more appropriate since they provide a better description of the population dynamics. In fact, discrete models often yield richer and more realistic results than continuous models. Moreover, since many continuous models cannot be solved analytically, using difference equations for approximation and finding solutions is a practical approach. Discrete-time models are widely used in population biology and complex ecosystems to examine taxonomic groups of organisms and species with the passage of time. These models are also well-suited for describing the chaotic behavior of nonlinear dynamics.
Fractional calculus is a branch of mathematics that studies the generalization of traditional calculus to include non-integer order derivatives and integrals. The origins of fractional calculus can be traced back to the seventeenth century, with the work of mathematicians such as Leibniz and Euler. However, it was not until the nineteenth century that the concept of fractional differentiation and integration was introduced by Liouville, who investigated the fractional calculus of analytic functions. In the twentieth century, fractional calculus gained further attention as it proved to be useful in a wide range of fields, including physics, engineering, and biology. One of the most significant developments in the field occurred in the 1960s and 1970s, when mathematicians and scientists realized that fractional calculus could be used to model many physical systems that exhibit anomalous diffusion, such as transport in porous media and electrical conduction in disordered systems. Today, fractional calculus continues to be an active area of research, with applications in various fields such as signal processing, control theory, and finance. The study of fractional calculus involves understanding the properties and behaviors of fractional derivatives and integrals, as well as developing techniques for their computation and application. The history of fractional calculus highlights the importance of exploring new and unconventional mathematical concepts, as they can often lead to significant breakthroughs in science and technology. Fractional derivatives and integrals are powerful tools for modeling non-locality and memory effects, which are not adequately captured by integer-order calculus. In contrast to integer-order calculus, fractional derivatives and integrals possess a non-local character and represent a suitable approach for modeling phenomena that depend on memory.
In this paper, we explore the fractional modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting. We utilize the Caputo fractional-order derivative operator due to its numerous advantages as previously discussed. The updated system, based on the model proposed in [36], is presented below: \[\begin{aligned} \frac{dx}{dt}&=&x[t]\left(1- x[t] – \frac{a y[t]}{m + x[t]}-\frac{k}{c+x[t]}\right)\,,\\ \frac{ dy}{ dt}&=&r y[t]\left(1- \frac{b y[t]}{m + x[t]}\right)\,. \end{aligned}\]
In this model, the temporal dynamics with memory can only be captured by the fractional derivative. The fractional integral of order \(\beta \in R^+\) of the function \(f(t),t>0,\) is defined as \[I^{\beta }f(t)=\int_0{}^t\frac{(t-s)^{\beta-1}}{\Gamma (\beta )}f(s) ds,\] and the fractional derivative of order \(\alpha\in(n-1,n)\) of \(f(t),t>0,\) is defined as \[^C D_t^{\alpha }f(t)=I^{n-\alpha }D_t{}^nf(t),\] where \(D_t=\frac{d}{ dt}.\) Therefore,
\[^CD_t^{\alpha }f(t)=\frac{1}{\Gamma (n-\alpha )}\int _0{}^t(t-s)^{n-\alpha -1}f^{(n)}(s) ds.\]
Using the caputo derivative, instead of the classical one, we get, \[\label{s1.1}\begin{cases} ^CD_t^{\theta }x(t)=x\left(1- x – \frac{a y}{m + x}-\frac{k}{c+x}\right),\\ ^CD_t^{\theta }y(t)=r y\left(1-\frac{b y}{m + x}\right)\,, \end{cases}\tag{1}\] where, \(^CD_t^{\theta}\) is the fractional order derivative operator of Caputo type of order \(\theta\).
The investigation presented in this paper focuses on a modified Leslie-Gower predator-prey model with fractional discrete-time Michaelis-Menten type prey harvesting. The analysis reveals the occurrence of nonnegative interior fixed points and their stability dynamics. Using the center manifold theorem and bifurcation theory, we derive conditions for flip and Neimark-Sacker bifurcations. The theoretical findings are consistently demonstrated through numerical simulations conducted with a computer package. Overall, our study highlights the importance of incorporating fractional calculus in predator-prey systems with harvesting and sheds light on the complex dynamics that arise in such models.
We will now establish the existence and uniqueness of the solution for the fractional system discussed earlier. To do this, we consider the initial value problem (IVP): \[^CD_t^{\theta }x(t)=f_x(t,x),,\] with initial condition \(x(0)=x_0\).
By utilizing the Volterra-type integral equation for the aforementioned initial value problem (IVP), we derive: \[x(t) = x_0 +\frac{1}{\Gamma (\theta )}\int _0{}^t(t-\mu )^{\theta -1}f_x(\mu ,x) d\mu,.\]
To ensure the existence of a solution for this IVP, we refer to a lemma proposed by Katugampola [6]:
Lemma 1. [Existence of Solution of IVP-Katugampola] For the model described earlier and under the hypotheses of Theorem 1, the function \(x(t) \in [0,T]\) is a solution of the initial value problem (IVP) \[^CD_t^{\theta }x(t)=f_x(t,x),,\] subject to \(x(0)=x_0\), if and only if it is a solution of the nonlinear Volterra integral equation given by \[x(t) = x_0 +\frac{1}{\Gamma (\theta )}\int _0{}^t(t-\mu )^{\theta -1}f_x(\mu ,x) d\mu\,.\]
We will now examine the existence of a solution for the IVP based on the theorem presented by [36,37]:
Theorem 1. [Existence] Let \(0 < \theta \leq 1\), \(x_0 \in \mathbb{R}\), \(\mathcal{K} > 0\), and \(T^* > 0\). Consider the function \(f_x: [0,T] \times [x_0-\mathcal{K},x_0+\mathcal{K}] \rightarrow \mathbb{R}\), which is continuous on the compact set \(P := {(t,x): t \in [0,T], x \in [x_0-\mathcal{K},x_0+\mathcal{K}]}\). Set \(M_x := \sup_{(t,x) \in P} |f_x(t,x)|\) and \[\label{e2} T = \begin{cases} T^* & \text{if}\ M_x = 0, \\ \min(T^*, (\mathcal{K} \Gamma(\theta + 1)/M_x)^{1/\theta}) & \text{otherwise}. \end{cases}\tag{2}\] Then, there exists a function \(x \in C[0,T]\) that solves the IVP \(^CD_t^{\theta}x = f_x(t,x)\), \(x(0) = x_0\).
Note that \(P\) is a compact set since it is closed and bounded in \(\mathbb{R}^2\). The function \(f_x\) is continuous on \(P\) and \(M_x\) is well-defined since \(P\) is compact. Hence, the conditions of the theorem are satisfied and a solution \(x\) exists for the IVP.
Katugampola [6] discusses the uniqueness of solutions for the fractional system, and we state the following theorem:
Theorem 2. [Uniqueness] Let \(x(0) \in \mathbb{R}\), \(\mathcal{K} > 0\), and \(T^* > 0\). Consider a continuous function \(f_x: P \rightarrow \mathbb{R}\) that satisfies a Lipschitz condition with respect to the second variable, i.e., \[|f_x(t,x_1) – f_x(t,x_2)| \leq \mathcal{L}|x_1 – x_2|,\] for some constant \(\mathcal{L} > 0\) that is independent of \(t\), \(x_1\), and \(x_2\), and let \(0 < \theta \leq 1\) with \(m = \lceil \theta \rceil\). Then, the initial value problem (IVP) \(, ^CD_t^{\theta}x = f_x(t,x)\), \(x(0) = x_0\) and \(T\) as defined in Theorem 1 has a unique solution \(x \in C[0,T]\).
Let us discuss the process of discretization, which has been previously introduced in the literature [5,6, 37,38], for differential equations involving fractional orders. In this study, we will employ this technique for modeling the fractional glycolysis. We will discretize the system using a method that involves arguments with piecewise constants.
To begin, we consider \(t\) satisfying the condition \(0 \leq t < h\), which implies that \(0 \leq \frac{t}{h} < 1\). This allows us to express the discretization of the system with the following equations:
\[\begin{aligned} ^CD_t^{\theta }x(t)&=&x\left(\left[\frac{t}{h}\right]h\right)\left(1- x\left(\left[\frac{t}{h}\right]h\right) – \frac{a y\left(\left[\frac{t}{h}\right]h\right)}{m x\left(\left[\frac{t}{h}\right]h\right)}- \frac{k}{c+ x\left(\left[\frac{t}{h}\right]h\right)}\right),\\ ^CD_t^{\theta }y(t)&=&r y\left(\left[\frac{t}{h}\right]h\right)\left(1-\frac{b y\left(\left[\frac{t}{h}\right]h\right)}{m + x\left(\left[\frac{t}{h}\right]h\right)}\right), \end{aligned}\] where \([\cdot]\) denotes the integer part function. Using the above equations and the condition on \(t\), we can simplify the solution to obtain:
\[\begin{aligned} x_1&=&x_0+ \frac{h^{\theta }}{\Gamma (1+\theta )}x_0\left(1- x_0 – \frac{a y_0}{m + x_0}- \frac{k}{c+ x_0}\right),\\ y_1&=&y_0+ \frac{h^{\theta }}{\Gamma (1+\theta )}r y_0\left(1-\frac{b y_0}{m + x_0}\right). \end{aligned}\]
Next, we consider \(h \leq t < 2h\), which means \(1 \leq \frac{t}{h} < 2\). Using this, we get:
\[\begin{aligned} x_2&=&x_1+ \frac{(t-h)^{\theta }}{\Gamma (1+\theta )}x_1\left(1- x_1 – \frac{a y_1}{m + x_1}- \frac{k}{c+ x_1}\right),\\ y_2&=&y_1+ \frac{h^{\theta }}{\Gamma (1+\theta )}r y_1\left(1-\frac{b y_1}{m + x_1}\right). \end{aligned}\]
Repeating this process \(n\) times yields: \[\begin{aligned} x_{n+1}&=&x_n+ \frac{(t- nh)^{\theta }}{\Gamma (1+\theta )}x_n\left(1- x_n – \frac{a y_n}{m + x_n}- \frac{k}{c+ x_n}\right),\\ y_{n+1}&=&y_n+ \frac{(t- nh)^{\theta }}{\Gamma (1+\theta )}r y_n\left(1-\frac{b y_n}{m + x_n}\right), \end{aligned}\] where, \(nh\leq t<(n+1)h\). For \(t\rightarrow(n+1)h\), system is reduced to \[\label{e3} \begin{cases} x_{n+1}=x_n+ \frac{h^{\theta }}{\Gamma (1+\theta )}x_n\left(1- x_n – \frac{a y_n}{m + x_n}- \frac{k}{c+ x_n}\right),\\ y_{n+1}=y_n+ \frac{h^{\theta }}{\Gamma (1+\theta )}r y_n\left(1-\frac{b y_n}{m + x_n}\right). \end{cases}\tag{3}\]
Remark 1. If the fractional parameter \(\theta\) approaches one in the above equation, the forward Euler discretization of our system is obtained.
In order to find the fixed points, we solve the following system. \[\begin{aligned} x &=& x+ \frac{h^{\theta }}{\Gamma (1+\theta )}x\left(1- x – \frac{a y}{m + x}- \frac{k}{c+ x}\right),\\ y&=&y+ \frac{h^{\theta }}{\Gamma [1+\theta ]}r y\left(1-\frac{b y}{m + x}\right). \end{aligned}\] The fixed points are
\[\begin{aligned} &\left\{E_0, E_1, E_2, E_3, E_m, E_p\right\}\\ & =\left\{\{0, 0\}, \left\{\frac{1}{2} \left(1-c-\sqrt{(1+c)^2-4 h}\right), 0\right\}, \right. \left.\left\{\frac{1}{2} \left(1-c+\sqrt{(1+c)^2-4 h}\right), 0\right\}, \left\{0, \frac{m}{\beta }\right\}, \left\{x_m, y_m\right\}, \left\{x_p, y_p\right\}\right\}, \end{aligned}\]
where \[\begin{aligned} x_m&=&\frac{1- \frac{a}{b}-c-\sqrt{\left(\frac{a}{b}-1-c\right)^2-4k}}{2},\\ x_p&=&\frac{1- \frac{a}{b}-c+\sqrt{\left(\frac{a}{b}-1-c\right)^2-4k}}{2},\\ y_m&=&\frac{m+x_m}{b},\\ y_p&=&\frac{m+x_p}{b}. \end{aligned}\] The Jacobian matrix of the system is: \[J = \left( \begin{array}{cc} 1+\frac{h^{\theta } x \left(-1+\frac{k}{(c+x)^2}+\frac{a y}{(m+x)^2}\right)}{\Gamma [1+\theta ]}+\frac{h^{\theta } \left(1-x-\frac{k}{c+x}-\frac{a y}{m+x}\right)}{\Gamma [1+\theta ]} & -\frac{a h^{\theta } x}{(m+x) \Gamma [1+\theta ]} \\ \frac{b h^{\theta } r y^2}{(m+x)^2 \Gamma [1+\theta ]} & 1-\frac{b h^{\theta } r y}{(m+x) \Gamma [1+\theta ]}+\frac{h^{\theta } r \left(1-\frac{b y}{m+x}\right)}{\Gamma [1+\theta ]} \\ \end{array} \right)\,.\] To determine the properties and topology of the fixed points mentioned earlier, we will utilize the following lemma, which can be found in textbooks on discrete dynamical systems.
Lemma 2. [Stability Lemma 1] Let \(\tau = Tr(J)\), \(\Delta = Det(J)\), and \(p(\lambda) = \lambda^2 – \tau \lambda + \Delta\), where \(\lambda_1\) and \(\lambda_2\) are the roots of \(p(\lambda)\). Then:
\(\left|\lambda_{1,2}\right| < 1\) if and only if \(p(-1) > 0\) and \(\Delta < 1\).
\(\left|\lambda_{1,2}\right| > 1\) if and only if \(p(-1) > 0\) and \(\Delta > 1\).
\(\left|\lambda_1\right| < 1\) and \(|\lambda_2| > 1\) (or vice versa) if and only if \(p(-1) < 0\).
\(\lambda_1 = -1\) and \(\left|\lambda_2\right| \neq 1\) if and only if \(p(-1) = 0\) and \(\tau \neq -2,0.\)
\(\lambda_{1,2} \in \mathbb{C}\) and \(\left|\lambda_{1,2}\right| = 1\) if and only if \(4\Delta – \tau^2 > 0\) and \(\Delta = 1\).
It should be noted that if \(\lambda_{1,2}\) are the eigenvalues of the 2 by 2 Jacobian matrix, the following lemma holds:
Lemma 3. [Stability Lemma 2] A fixed point is referred to as:
a sink if \(\left|\lambda_{1,2}\right|<1\), indicating local asymptotic stability.
a source if \(\left|\lambda_{1,2}\right|>1\), indicating local instability.
a saddle if \(\left|\lambda_1\right|<1\) and \(|\lambda_2|>1\) (or \(\left|\lambda_1\right|>1\) and \(\left|\lambda_2\right|<1\)).
non-hyperbolic if either \(\left|\lambda_1\right|=1\) or \(\left|\lambda_2\right|=1\), but not both.
To determine the stability of the fixed points, we will evaluate \(J\) at each of the boundary fixed points \(E_0\), \(E_1\), \(E_2\), and \(E_3\), as well as the positive interior fixed points \(E_m\) and \(E_p\). \[J_0 = J|_{(0,0)}=\left( \begin{array}{cc} 1+\frac{h^{\theta }}{\Gamma [1+\theta ]}\left(1-\frac{k}{c}\right) & 0 \\ 0 & 1+\frac{h^{\theta } r}{\Gamma [1+\theta ]} \\ \end{array} \right)\] and the corresponding eigenvalues are \(\left\{1+\frac{h^{\theta }}{\Gamma [1+\theta ]}r,1+\frac{h^{\theta}}{\Gamma [1+\theta ]}\left(\frac{c-k}{c}\right)\right\}.\) Thus the fixed point is saddle if \(k > c,\) unstable if \(k< c\) and non- hyperbolic if \(k = c.\) \[J_{1,2} = J|_{E_1, E_2}=\left( \begin{array}{cc} 1+\frac{h^{\theta }}{\Gamma [1+\theta ]}x_{1,2} \left(-1+\frac{k}{\left(c+x_{1,2}\right){}^2}\right) & -\frac{h^{\theta }}{\Gamma [1+\theta ]}\frac{x_{1,2} a}{m+x_{1,2}} \\ 0 & 1+\frac{h^{\theta } r}{\Gamma [1+\theta ]} \\ \end{array} \right)\] and the corresponding eigenvalues are \(\left\{1+\frac{h^{\theta }}{\Gamma [1+\theta ]}r, 1+\frac{h^{\theta}}{\Gamma [1+\theta ]}x_{1,2}\left(\frac{k}{\left(c+x_{1,2}\right){}^2}-1\right)\right\}.\) Thus, for both boundary fixed points \(E_1\) and \(E_2\), if \(k<\left(c+x_{1,2}\right)^2\), i-e, if \(0<c<1 \&\& c<k\leq \frac{(1+c)^2}{4}\), then the fixed point is saddle. If \(k>\left(c+x_{1,2}\right)^2,\) i-e, \((0<c\leq 1\&\&0<k<c)\left\|\left(c>1\&\&0<k\leq \frac{(1+c)^2}{4}\right)\right.\), then the fixed point is unstable. If \(k=\left(c+x_{1,2}\right)^2,\) the the fixed point may undergo transcritical or fold bifurcation and if \(k = \left(1 -\frac{2\Gamma [1+\theta ]}{h^{\theta }x_{1,2}}\right)\left(c+x_{1,2}\right)^2,\) then the fixed point undergoes period- douling bifurcation. The possibility of Neimark-Sacker bifurcation is mute for these fixed points. \[J_3 = J|_{\left(0, \frac{m}{\beta }\right)}=\left( \begin{array}{cc} 1+\frac{h^{\theta }}{\Gamma [1+\theta ]} \left(1-\frac{k}{c}-\frac{a}{b}\right) & 0 \\ \frac{h^{\theta }}{\Gamma [1+\theta ]}\frac{r}{b} & 1-\frac{h^{\theta }}{\Gamma [1+\theta ]}r \\ \end{array} \right)\] and the corresponding eigenvalues are \(\left\{1+\frac{h^{\theta }}{\Gamma [1+\theta ]} \left(1-\frac{k}{c}-\frac{a}{b}\right),1-\frac{h^{\theta }}{\Gamma [1+\theta ]} r\right\}\). Therefore if \(k<c\left(1-\frac{a}{b}\right)\) the the fixed point is saddle, if \(k>c\left(1-\frac{a}{b}\right)\) the fixed point is stable, if \(k=c\left(1-\frac{a}{b}\right)\) the fixed point may undergo transcritical or fold bifurcation and if \(k = c\left(1-\frac{a}{b}+\frac{2\Gamma [1+\theta ]}{h^{\theta }}\right),\) the fixed point undergoes period-douling bifurcation. The possibility of Neimark-Sacker bifurcation is mute for this fixed point also.
For the interior fixed points the analysis of stability is the same and we will perform it under the generic variable name \(x_{m,p}=x\) and \(y_{m,p}=y\). Let the Jacobian matrix of the system evaluated at \(E_{m, p}\) be \[\bar{J}=\left( \begin{array}{cc} 1+\frac{h^{\theta } }{\Gamma [1+\theta ]}x \left(-1+\frac{k}{(c+x)^2}+\frac{a y}{(m+x)^2}\right) & -\frac{h^{\theta } }{\Gamma [1+\theta ]}\frac{a x}{(m+x)} \\ \frac{h^{\theta }}{\Gamma [1+\theta ]}\frac{r y}{(m+x)} & 1-\frac{h^{\theta }}{\Gamma [1+\theta ]}r \\ \end{array} \right)\,.\]
Theorem 3. [Stability of Positive Interior Fixed Points] \(p(\lambda ) = \lambda ^2-\tau \lambda + \Delta\) be the characteristic polynomial for the jacobian matrix \(\bar{J}\) in (), \(\tau=tr\left(\bar{J} \right)\) and \(\Delta=Det\left(\bar{J} \right).\) If \[\begin{aligned} h_1&=&\Gamma [1+\theta ]^{\frac{1}{\theta }}\left(\frac{r+x-\frac{k x}{(c+x)^2}-\frac{a x y}{(m+x)^2}-\sqrt{\left(r+x-\frac{k x}{(c+x)^2}-\frac{a x y}{(m+x)^2}\right)^2-4r x\left(\frac{k}{(c+x)^2}-1\right)}}{r x\left(\frac{k}{(c+x)^2}-1\right)}\right)^{\frac{1}{\theta }},\\ h_2&=&\Gamma [1+\theta ]^{\frac{1}{\theta }}\left(\frac{r+x-\frac{k x}{(c+x)^2}-\frac{a x y}{(m+x)^2}+\sqrt{\left(r+x-\frac{k x}{(c+x)^2}-\frac{a x y}{(m+x)^2}\right)^2-4r x\left(\frac{k}{(c+x)^2}-1\right)}}{r x\left(\frac{k}{(c+x)^2}-1\right)}\right)^{\frac{1}{\theta }} \end{aligned}\] and \[h_{\Delta }= e^{-\frac{i \pi }{\theta }} \Gamma [1+\theta ]^{\frac{1}{\theta }}\left(\frac{x \left(-1+\frac{a y}{(m+x)^2}+\frac{k}{(c+x)^2}\right)-r}{r x\left(\frac{k}{(c+x)^2}-1\right)}\right)^{\frac{1}{\theta }}\] then,
If \(k\) is greater than \((c+x)^2\), then the interior fixed point is locally asymptotically stable if \(h\) belongs to the interval \(\left(\left(0, h_1\right) \cup \left(h_2, \infty \right)\right)\cap \left(0,h_{\Delta }\right)\); otherwise, it is locally asymptotically stable if \(h\) belongs to the interval \(\left(h_1, h_2\right)\cap \left(0,h_{\Delta }\right)\).
The interior fixed point is locally unstable if \(h\) belongs to the interval \(\left(\left(0, h_1\right) \cup \left(h_2, \infty \right)\right)\cap \left(h_{\Delta },\infty \right)\).
The interior fixed point is a saddle if \(h\) belongs to the interval \(\left(h_1, h_2\right)\).
The interior fixed point is non-hyperbolic and has eigenvalues with \(\lambda_1=-1\) and \(\left| \lambda 2\right| \neq 1\) if and only if \(h=h{1}\) or \(h_2\) and \(h\) does not belong to the set \(\left\{\left(\frac{2\Gamma(1+\theta )}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta }}, \left(\frac{4\Gamma (1+\theta )}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta }}\right\}\).
The interior fixed point is non-hyperbolic and has complex conjugate eigenvalues with \(\left| \lambda _1\right| = \left| \lambda 2\right| = 1\) if and only if \(h=h{\Delta}\) and \(h\) belongs to the interval \(\left(0,\left(\frac{4\Gamma (1+\theta )}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta}}\right)\).
Proof. Let \(p(\lambda)=\lambda^2-\tau\lambda+\Delta\) be the characteristic polynomial for the jacobian matrix \(\bar{J}\), where \[\tau=2+\frac{h^{\theta}}{\Gamma[1+\theta]}\left(x\left(-1+\frac{k}{(c+x)^2}+\frac{ay}{(m+x)^2}\right)-r\right)\] and \[\Delta=1+\frac{h^{\theta}}{\Gamma[1+\theta]}\left(x\left(-1+\frac{ay}{(m+x)^2}+\frac{k}{(c+x)^2}\right)-r\right)+rx\left(\frac{k}{(c+x)^2}-1\right)\frac{h^{2\theta } }{\Gamma [1+\theta ]^2}.\] Then by definition of \(h_1\) and \(h_2\), if \(k>(c+x)^2\) then \(h_{1,2}\in\mathbb{R}\) if \(\left(r+x-\frac{k x}{(c+x)^2}-\frac{a x y}{(m+x)^2}\right)^2\geq4rx\left(\frac{k}{(c+x)^2}-1\right)\) and \(p(-1)=0\) if and only if \(h = h_1\) or \(h_2\); \(p(-1) < 0\) if and only if \(h \in \left(h_1, h_2\right)\); \(p(-1) > 0\) if and only if \(h \in \left(0, h_1\right) \cup \left(h_2, \infty \right)\). On the other hand, if \(k<(c+x)^2\) then \(h_{1,2} \in \mathbb{R}\) and \(p(-1) = 0\) if and only if \(h = h_1\) or \(h_2\); \(p(-1) > 0\) if and only if \(h \in \left(h_1, h_2\right)\); \(p(-1) < 0\) if and only if \(h \in \left(0, h_1\right) \cup \left(h_2, \infty \right)\) and \(\tau \neq -2, 0\) if and only if \(h\notin \left\{\left(\frac{2\Gamma (1+\theta )}{r-x \left(-1+\frac{k}{(c+x)^2}+\frac{ay}{(m+x)^2}\right)}\right)^{\frac{1}{\theta }}, \left(\frac{4\Gamma (1+\theta )}{r-x \left(-1+\frac{k}{(c+x)^2}+\frac{a y}{(m+x)^2}\right)}\right)^{\frac{1}{\theta }}\right\}.\) Finally, \(-2<\tau <2\) if \(0<h<\left(\frac{4\Gamma(1+\theta )}{r-x \left(\frac{a y}{(m+x)^2}+\frac{k}{(c+x)^2}-1\right)}\right)^{\frac{1}{\theta }}\) and \(\Delta=1\) if \(h = h_{\Delta }\); \(\Delta > 1\) if \(h > h_{\Delta}\); \(\Delta < 1\) if \(h < h_{\Delta }\). Thus,
If the value of \(k\) is greater than \((c+x)^2\), then the interior fixed point is locally asymptotically stable if \(h\) belongs to the interval \((0, h_{\Delta})\) and is either in the interval \((0, h_1)\) or \((h_2, \infty)\), otherwise it is locally asymptotically stable if \(h\) belongs to the interval \((h_1, h_2)\cap(0, h_{\Delta})\).
The interior fixed point is locally unstable if \(h\) belongs to the interval \((h_{\Delta}, \infty)\cap(0, h_1)\cup(h_2, \infty)\).
The interior fixed point is a saddle point if \(h\) belongs to the interval \((h_1, h_2)\).
The interior fixed point is non-hyperbolic and has eigenvalues such that \(\lambda_1=-1\) and \(\left| \lambda 2\right| \neq 1\), if and only if \(h\) equals \(h_1\) or \(h_2\) and is not equal to either \(\left(\frac{2\Gamma(1+\theta)}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta}}\) or \(\left(\frac{4\Gamma(1+\theta)}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta}}\).
The interior fixed point is non-hyperbolic and has complex conjugate eigenvalues such that \(\left|\lambda_1\right|=\left|\lambda_2\right|=1\), if and only if \(h\) equals \(h{\Delta}\) and belongs to the interval \((0, \left(\frac{4\Gamma(1+\theta)}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta}})\).
◻
Bifurcation is a fundamental concept in dynamical systems theory that describes the qualitative changes that occur in a system as a parameter is varied. The basic idea is that the behavior of the system can change abruptly as the parameter crosses a certain threshold value. There are several types of bifurcations that can occur, including saddle-node bifurcation, pitchfork bifurcation, transcritical bifurcation, Hopf bifurcation, and period-doubling bifurcation. Each type of bifurcation has its own characteristic behavior and can lead to different types of dynamical behavior, such as limit cycles, chaos, and multistability. Understanding bifurcations is crucial for analyzing the behavior of complex systems and predicting how they will respond to changes in their environment or parameters [39,40].
Let \(M_{PD}=\left\{(a, b, c,h, k,m, r,
\theta )\in \mathbb{R}_+^7:h \in \left\{h_1, h_2\right\}, h\notin
\left\{\left(\frac{2\Gamma (1+\theta )}{r+x-\frac{a x
y}{(m+x)^2}}\right)^{\frac{1}{\theta }}, \left(\frac{4\Gamma (1+\theta
)}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta
}} \right\}\right\}\). Let \(h\)
be the bifurcation parameter. Then, variation of parameters in small
neighborhood of \(M_{PD}\) gives
emergence of period doubling bifurcation. Let \(k\in M_{PD}\) and let \(H\) be the perturbation of \(h\) where \(|H|
< < < 1\). The system can be written as \[\left(
\begin{array}{c}
x \\
y \\
\end{array}
\right) \to \left(
\begin{array}{c}
x+\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}x\left(1- x – \frac{a y}{m
+ x}- \frac{k}{c+ x}\right) \\
y+\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}r y\left(1-\frac{b y}{m +
x}\right) \\
\end{array}
\right).\] Translate the fixed point to \((0, 0).\) Define \(X=x-\bar{x}\) and \(Y =y-\bar{y}\). Then, the above system can
be written as \[\left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) \to \left(
\begin{array}{c}
X+\frac{(h+H)^{\theta } \left(X+\bar{x}\right)
\left(1-X-\bar{x}-\frac{k}{c+X+\bar{x}}-\frac{a
\left(Y+\bar{y}\right)}{m+X+\bar{x}}\right)}{\Gamma
[1+\theta ]} \\
Y+\frac{(h+H)^{\theta } r \left(Y+\bar{y}\right) \left(1-\frac{b
\left(Y+\bar{y}\right)}{m+X+\bar{x}}\right)}{\Gamma [1+\theta ]} \\
\end{array}
\right).\] If we define,
\(a_{11}=1+\frac{h^{\theta }}{\Gamma [1+\theta
]}\bar{x} \left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^2}\right);\)
\(a_{12}=-\frac{h^{\theta}}{\Gamma[1+\theta]}\frac{a\bar{x}}{\left(m+\bar{x}\right)};\)
\(b_1=\frac{h^{\theta }}{\Gamma [1+\theta
]}\left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^2}+\bar{x}
\left(-\frac{k}{\left(c+\bar{x}\right)^3}-\frac{a
\bar{y}}{\left(m+\bar{x}\right)^3}\right)\right);\)
\(b_2=-\frac{h^{\theta } }{\Gamma [1+\theta
]}\frac{a m}{\left(m+\bar{x}\right)^2};\)
\(b_3=\frac{h^{-2+\theta } (-1+\theta )
\theta \left(\bar{x}
\left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^2}\right)\right)}{2\Gamma [1+\theta
]}\);
\(b_4 =-\frac{a h^{-1+\theta }
\theta \bar{x}}{\left(m+\bar{x}\right) \Gamma [1+\theta
]}\);
\(b_5=0;\)
\(b_6 = \frac{h^{\theta}}{\Gamma [1+\theta
]}\left(-\frac{k}{\left(c+\bar{x}\right)^3}-\frac{a
\bar{y}}{\left(m+\bar{x}\right)^3}+\bar{x}
\left(\frac{k}{\left(c+\bar{x}\right)^4}+\frac{a\bar{y}}{\left(m+\bar{x}\right)^4}\right)\right);\)
\(b_7=\frac{h^{\theta}}{\Gamma[1+\theta]}\frac{am}{\left(m+\bar{x}\right)^3};\)
\(b_8 = \frac{h^{-1+\theta }
\theta \left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^2}+\bar{x}
\left(-\frac{k}{\left(c+\bar{x}\right)^3}-\frac{a\bar{y}}{\left(m+\bar{x}\right)^3}\right)\right)}{\Gamma
[1+\theta ]};\)
\(b_9 = -\frac{h^{\theta } }{\Gamma [1+\theta
]}\frac{a h^{-1} m \theta}{\left(m+\bar{x}\right)^2};\)
\(b_{10} = \frac{h^{-2+\theta } (-1+\theta )
\theta \left(\bar{x}
\left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^2}\right)\right)}{2 \Gamma [1+\theta
]};\)
\(b_{11}=-\frac{a h^{-2+\theta } (-1+\theta )
\theta \bar{x}}{2 \left(m+\bar{x}\right)\Gamma [1+\theta
]};\)
\(b_{12}=0;\)
\(b_{13}=0;\)
\(b_{14}=0;\)
Then, \[\begin{aligned}
f^1_{PD}(X, Y, H) =& b_1 X^2+ b_2 X Y+ b_3 H X + b_4 H
Y+b_5Y^2+b_6X^3+ b_7X^2 Y + b_8 H X^2+ b_9H
X Y \\&+ b_{10}H^2 X + b_{11}H^2Y + b_{12} X Y^2+ b_{13}H Y^2
+b_{14}Y^3+ O\left(\left|H + X + Y|^4\right.\right),
\end{aligned}\] and \[X\to a_{11} X
+a_{12}Y + f^1_{ PD}(X, Y, H).\] Similarly, we can write \(Y\to a_{21}X+a_{22}Y+f^2_{ PD}(X, Y, H)\)
by defining
\(a_{21} =\frac{h^{\theta }}{\Gamma [1+\theta
]}\frac{b r \bar{y}^2}{\left(m+\bar{x}\right)^2}\);
\(a_{22} = 1-\frac{h^{\theta }}{\Gamma
[1+\theta]}r;\)
\(b_{15} = -\frac{h^{\theta }}{\Gamma
[1+\theta ]}\frac{b r
\bar{y}^2}{\left(m+\bar{x}\right)^3};\)
\(b_{16}=\frac{h^{\theta }}{\Gamma[1+\theta
]}\frac{2 b r \bar{y}}{\left(m+\bar{x}\right)^2};\)
\(b_{17}=\frac{h^{-1+\theta }}{\Gamma
[1+\theta ]}\frac{br\theta
\bar{y}^2}{\left(m+\bar{x}\right)^2};\)
\(b_{18} = -\frac{h^{-1+\theta }}{\Gamma
[1+\theta ]}r \theta ;\)
\(b_{19} = -\frac{b h^{\theta}
r}{\left(m+\bar{x}\right) \Gamma [1+\theta ]};\)
\(b_{20} = \frac{h^{\theta }}{\Gamma [1+\theta
]}\frac{b r \bar{y}^2}{\left(m+\bar{x}\right)^4};\)
\(b_{21} = -\frac{h^{\theta }}{\Gamma
[1+\theta]}\frac{2 b r
\bar{y}}{\left(m+\bar{x}\right)^3};\)
\(b_{22} =-\frac{h^{-1+\theta }}{\Gamma
[1+\theta ]}\frac{b r
\theta \bar{y}^2}{\left(m+\bar{x}\right)^3}\);
\(b_{23} = \frac{h^{-1+\theta }}{\Gamma
[1+\theta ]}\frac{2 b r
\theta \bar{y}}{\left(m+\bar{x}\right)^2};\)
\(b_{24} = \frac{h^{-2+\theta
}}{\Gamma[1+\theta ]}\frac{b r (-1+\theta ) \theta \bar{y}^2}{2
\left(m+\bar{x}\right)^2};\)
\(b_{25} = -\frac{h^{-2+\theta }}{2\Gamma
[1+\theta ]}r (-1+\theta) \theta ;\)
\(b_{26} = \frac{h^{\theta }}{\Gamma [1+\theta
]}\frac{b r}{\left(m+\bar{x}\right)^2};\)
\(b_{27} = -\frac{b h^{-1+\theta } r \theta
}{\left(m+\bar{x}\right)\Gamma [1+\theta ]}\);
\(b_{28} = 0;\)
and
\[\begin{aligned}
f^2_{PD}(X, Y, H)=&b_{15}X^2+ b_{16}X Y+ b_{17}H X + b_{18}H
Y+b_{19}Y^2+b_{20}X^3+ b_{21}X^2 Y + b_{22}H X^2+ b_{23}H X Y
\\&+ b_{24}H^2 X + b_{25}H^2Y + b_{26}X Y^2+ b_{27}H Y^2 +b_{28}Y^3+
O\left(\left|H + X + Y|^4\right.\right).
\end{aligned}\] Thus, the system can be written as \[\left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) \to \left(
\begin{array}{cc}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{array}
\right) \left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) + \left(
\begin{array}{c}
f^1_{ PD}(X, Y, H) \\
f^2_{ PD}(X, Y, H) \\
\end{array}
\right).\] Let \(T =\left(
\begin{array}{cc}
a_{12} & a_{12} \\
-1- a_{11} & \lambda _2 – a_{22} \\
\end{array}
\right)\) be an invertable transformation matrix such that \(\left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) \to T\left(
\begin{array}{c}
\mu \\
\eta \\
\end{array}
\right)\)
The transformed system is given by \[\left(
\begin{array}{c}
\mu \\
\eta \\
\end{array}
\right) \to \left(
\begin{array}{cc}
-1 & 0 \\
0 & \lambda _2 \\
\end{array}
\right)\left(
\begin{array}{c}
\mu \\
\eta \\
\end{array}
\right) + \left(
\begin{array}{c}
g^1_{ PD}(X, Y, H) \\
g^2_{ PD}(X, Y, H) \\
\end{array}
\right)\] where \[\begin{aligned}
g^1_{ PD}(\mu , \eta ,H) =& d_1 \mu ^2 + d_2 \mu \eta + d_3 H
\mu + d_4 H \eta + d_5 H^2+d_6 \eta ^2 + d_7 \mu ^3 + d_8 \mu ^2\eta
+ d_9 H \mu ^2 + d_{10} H \mu \eta \\
&+ d_{11}H^2 \mu + d_{12} H^2 \eta + d_{13} \mu \eta ^2 +
d_{14}H \eta ^2 + d_{15} \eta ^3
+ O\left(\left|H + \mu + \eta |^4\right.\right)\\
g^2_{ PD}(\mu , \eta ,H) =& d_{16} \mu ^2 + d_{17} \mu \eta +
d_{18} H \mu + d_{19} H \eta +d_{20} H^2+d_{21} \eta ^2 + d_{22} \mu
^3 + d_{23} \mu ^2\eta + d_{24} H \mu ^2 \\
&+ d_{25} H \mu \eta + d_{26}H^2 \mu + d_{27} H^2 \eta + d_{28}
\mu \eta ^2 + d_{29}H
\eta ^2 + d_{30} \eta ^3 + O\left(\left|H + \mu + \eta
|^4\right.\right)
\end{aligned}\] and \[\begin{aligned}
d_1 = & a_{12}^2 c_1 \left(-b_{15}+b_1
c_2\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{16}+b_2
c_2\right)+\left(-1-a_{11}\right){}^2 c_1
\left(-b_{19}+b_5 c_2\right);\\
d_2 =& 2 a_{12}^2 c_1 \left(-b_{15}+b_1
c_2\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{16}+b_2
c_2\right)+a_{12} c_1 \left(-b_{16}+b_2
c_2\right) \left(-a_{22}+\lambda _2\right)\\&
+ 2 \left(-1-a_{11}\right) c_1 \left(-b_{19}+b_5 c_2\right)
\left(-a_{22}+\lambda _2\right);\\
d_3=& a_{12} c_1 \left(-b_{17}+b_3 c_2\right)+\left(-1-a_{11}\right)
c_1 \left(-b_{18}+b_4 c_2\right);\\
d_4 =& a_{12} c_1 \left(-b_{17}+b_3 c_2\right)+c_1 \left(-b_{18}+b_4
c_2\right) \left(-a_{22}+\lambda _2\right);\\
d_5 =& 0;\\
d_6 =& a_{12}^2 c_1 \left(-b_{15}+b_1 c_2\right)+a_{12} c_1
\left(-b_{16}+b_2 c_2\right) \left(-a_{22}+\lambda _2\right)+c_1
\left(-b_{19}+b_5
c_2\right) \left(-a_{22}+\lambda _2\right)^2;\\
d_7 =& a_{12}^3 c_1 \left(-b_{20}+b_6
c_2\right)+\left(-1-a_{11}\right) a_{12}^2 c_1 \left(-b_{21}+b_7
c_2\right)+\left(-1-a_{11}\right){}^2
a_{12} c_1 \left(-b_{26}+b_{12} c_2\right)\\&
+\left(-1-a_{11}\right){}^3 c_1 \left(-b_{28}+b_{14} c_2\right);\\
d_8 = & 3 a_{12}^3 c_1 \left(-b_{20}+b_6 c_2\right)+2
\left(-1-a_{11}\right) a_{12}^2 c_1 \left(-b_{21}+b_7
c_2\right)+\left(-1-a_{11}\right)^2
a_{12} c_1 \left(-b_{26}+b_{12} c_2\right)\\&
+a_{12}^2 c_1 \left(-b_{21}+b_7 c_2\right) \left(-a_{22}+\lambda
_2\right)+2 \left(-1-a_{11}\right) a_{12}
c_1 \left(-b_{26}+b_{12} c_2\right) \left(-a_{22}+\lambda
_2\right)\\&
+3 \left(-1-a_{11}\right)^2 c_1 \left(-b_{28}+b_{14} c_2\right)
\left(-a_{22}+\lambda _2\right);\\
d_9 = & a_{12}^2 c_1 \left(-b_{22}+b_8
c_2\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{23}+b_9
c_2\right)+\left(-1-a_{11}\right){}^2 c_1
\left(-b_{27}+b_{13} c_2\right);\\
d_{10} = & 2 a_{12}^2 c_1 \left(-b_{22}+b_8
c_2\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{23}+b_9
c_2\right)+a_{12} c_1 \left(-b_{23}+b_9
c_2\right) \left(-a_{22}+\lambda _2\right)\\&
+2 \left(-1-a_{11}\right) c_1 \left(-b_{27}+b_{13} c_2\right)
\left(-a_{22}+\lambda _2\right);\\
d_{11} = & a_{12} c_1 \left(-b_{24}+b_{10}
c_2\right)+\left(-1-a_{11}\right) c_1 \left(-b_{25}+b_{11} c_2\right);\\
d_{12} =& a_{12} c_1 \left(-b_{24}+b_{10} c_2\right)+c_1
\left(-b_{25}+b_{11} c_2\right) \left(-a_{22}+\lambda _2\right);\\
d_{13}=& 3 a_{12}^3 c_1 \left(-b_{20}+b_6
c_2\right)+\left(-1-a_{11}\right) a_{12}^2 c_1 \left(-b_{21}+b_7
c_2\right)+2 a_{12}^2 c_1 \left(-b_{21}+b_7
c_2\right) \left(-a_{22}+\lambda _2\right)\\&+
2 \left(-1-a_{11}\right) a_{12} c_1 \left(-b_{26}+b_{12}
c_2\right) \left(-a_{22}+\lambda _2\right)+a_{12}
c_1 \left(-b_{26}+b_{12} c_2\right) \left(-a_{22}+\lambda
_2\right)^2\\&+
3 \left(-1-a_{11}\right) c_1 \left(-b_{28}+b_{14} c_2\right)
\left(-a_{22}+\lambda _2\right)^2;\\
d_{14} =& a_{12}^2 c_1 \left(-b_{22}+b_8 c_2\right)+a_{12} c_1
\left(-b_{23}+b_9 c_2\right) \left(-a_{22}+\lambda _2\right)+c_1
\left(-b_{27}+b_{13}
c_2\right) \left(-a_{22}+\lambda _2\right){}^2;\\
d_{15}=& a_{12}^3 c_1 \left(-b_{20}+b_6 c_2\right)+a_{12}^2 c_1
\left(-b_{21}+b_7 c_2\right) \left(-a_{22}+\lambda _2\right)+a_{12}c_1
\left(-b_{26}+b_{12}c_2\right) \left(-a_{22}+\lambda
_2\right){}^2\\&
+c_1 \left(-b_{28}+b_{14} c_2\right) \left(-a_{22}+\lambda
_2\right){}^3;\\
d_{16} = & a_{12}^2 c_1 \left(-b_{15}+b_1
c_3\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{16}+b_2
c_3\right)+\left(-1-a_{11}\right){}^2
c_1 \left(-b_{19}+b_5 c_3\right);\\
d_{17} =& 2 a_{12}^2 c_1 \left(-b_{15}+b_1
c_3\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{16}+b_2
c_3\right)+a_{12} c_1 \left(-b_{16}+b_2
c_3\right) \left(-a_{22}+\lambda _2\right)\\&+
2 \left(-1-a_{11}\right) c_1 \left(-b_{19}+b_5 c_3\right)
\left(-a_{22}+\lambda _2\right);\\
d_{18} =& a_{12} c_1 \left(-b_{17}+b_3
c_3\right)+\left(-1-a_{11}\right) c_1 \left(-b_{18}+b_4 c_3\right);\\
d_{19} =& a_{12} c_1 \left(-b_{17}+b_3 c_3\right)+c_1
\left(-b_{18}+b_4 c_3\right) \left(-a_{22}+\lambda _2\right);\\
d_{20} =& 0;\\
d_{21} =& a_{12}^2 c_1 \left(-b_{15}+b_1 c_3\right)+a_{12} c_1
\left(-b_{16}+b_2 c_3\right) \left(-a_{22}+\lambda _2\right)+c_1
\left(-b_{19}+b_5
c_3\right) \left(-a_{22}+\lambda _2\right){}^2;\\
d_{22} =& a_{12}^3 c_1 \left(-b_{20}+b_6
c_3\right)+\left(-1-a_{11}\right) a_{12}^2 c_1 \left(-b_{21}+b_7
c_3\right)\\&
+\left(-1-a_{11}\right){}^2a_{12} c_1 \left(-b_{26}+b_{12}
c_3\right)+\left(-1-a_{11}\right){}^3 c_1 \left(-b_{28}+b_{14}
c_3\right);\\
d_{23} =& 3 a_{12}^3 c_1 \left(-b_{20}+b_6 c_3\right)+2
\left(-1-a_{11}\right) a_{12}^2 c_1 \left(-b_{21}+b_7
c_3\right)+\left(-1-a_{11}\right){}^2
a_{12} c_1 \left(-b_{26}+b_{12} c_3\right)\\&
+a_{12}^2 c_1 \left(-b_{21}+b_7 c_3\right) \left(-a_{22}+\lambda
_2\right)+2 \left(-1-a_{11}\right) a_{12}
c_1 \left(-b_{26}+b_{12} c_3\right) \left(-a_{22}+\lambda
_2\right)\\
&+3 \left(-1-a_{11}\right){}^2 c_1 \left(-b_{28}+b_{14}
c_3\right) \left(-a_{22}+\lambda _2\right);\\
d_{24} =& a_{12}^2 c_1 \left(-b_{22}+b_8
c_3\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{23}+b_9
c_3\right)+\left(-1-a_{11}\right){}^2
c_1 \left(-b_{27}+b_{13} c_3\right);\\
d_{25} =& 2 a_{12}^2 c_1 \left(-b_{22}+b_8
c_3\right)+\left(-1-a_{11}\right) a_{12} c_1 \left(-b_{23}+b_9
c_3\right)+a_{12} c_1 \left(-b_{23}+b_9
c_3\right) \left(-a_{22}+\lambda _2\right)\\
&+2 \left(-1-a_{11}\right) c_1 \left(-b_{27}+b_{13}
c_3\right) \left(-a_{22}+\lambda _2\right);\\
d_{26} = &a_{12} c_1 \left(-b_{24}+b_{10}
c_3\right)+\left(-1-a_{11}\right) c_1 \left(-b_{25}+b_{11} c_3\right);\\
d_{27} = &a_{12} c_1 \left(-b_{24}+b_{10} c_3\right)+c_1
\left(-b_{25}+b_{11} c_3\right) \left(-a_{22}+\lambda _2\right);\\
d_{28} = &3 a_{12}^3 c_1 \left(-b_{20}+b_6
c_3\right)+\left(-1-a_{11}\right) a_{12}^2 c_1 \left(-b_{21}+b_7
c_3\right)+2 a_{12}^2 c_1 \left(-b_{21}+b_7
c_3\right) \left(-a_{22}+\lambda _2\right)\\
&+2 \left(-1-a_{11}\right) a_{12} c_1 \left(-b_{26}+b_{12}
c_3\right) \left(-a_{22}+\lambda _2\right)+a_{12}
c_1 \left(-b_{26}+b_{12} c_3\right) \left(-a_{22}+\lambda
_2\right)^2\\
&+3 \left(-1-a_{11}\right) c_1 \left(-b_{28}+b_{14}
c_3\right) \left(-a_{22}+\lambda _2\right){}^2;\\
d_{29} =& a_{12}^2 c_1 \left(-b_{22}+b_8 c_3\right)+a_{12} c_1
\left(-b_{23}+b_9 c_3\right) \left(-a_{22}+\lambda _2\right)+c_1
\left(-b_{27}+b_{13}
c_3\right) \left(-a_{22}+\lambda _2\right){}^2;\\
d_{30} =& a_{12}^3 c_1 \left(-b_{20}+b_6 c_3\right)+a_{12}^2 c_1
\left(-b_{21}+b_7 c_3\right) \left(-a_{22}+\lambda _2\right)+a_{12} c_1
\left(-b_{26}+b_{12}c_3\right) \left(-a_{22}+\lambda _2\right){}^2\\
&+c_1 \left(-b_{28}+b_{14} c_3\right) \left(-a_{22}+\lambda
_2\right){}^3,
\end{aligned}\] and \[X = a_{12}(\mu
+\eta ), Y = -\left(1+ a_{11}\right)\mu + \left(\lambda _2 –
a_{22}\right)\eta .\] Define \(M_C=
\{(\mu , \eta ,H) | \eta = \mathcal{G}(\mu ,H)\},\) \(|\mu | < \delta _1,\) \(|H| < \delta _2,\) \(f_c(0,0) = 0,\) \(D f_c(0,0)=0\) and \[\mathcal{F}(\mathcal{G}(\mu ,H),H) =
\mathcal{G}\left(-\mu + g^1_{ PD}(\mu , \mathcal{G}(\mu ,H)
,H),H\right) – \lambda
_2 \mathcal{G}(\mu ,H) – g^2_{ PD}(\mu , \mathcal{G}(\mu ,H)
,H)\] Assume \(f_c(\mu ,H)= m_1 \mu ^2
+ m_2 H \mu + m_3 H^2 + O\left(\left|\mu +
H|^3\right.\right).\) By solving and comparing coefficients, we
get
\[m_1 = \frac{d_{16}}{1-\lambda _2}; m_2 = -\frac{d_{18}}{1+\lambda _2}; m_3 = 0.\]
Thus, \(f_c(\mu ,H)= \frac{d_{16}}{1-\lambda _2} \mu ^2 -\frac{d_{18}}{1+\lambda _2} H \mu + O\left(\left|\mu + H|^3\right.\right)\). The dynamics restricted to \(M_c\) are given locally by the map \[\begin{aligned} \label{e4}F_c :& \mu \rightarrow -\mu + d_1\mu ^2 +d_3H \mu +\left(d_7+\frac{d_2 d_{16}}{1-\lambda _2}\right)\mu ^3 +\left(d_9+\frac{d_4 d_{16}}{1-\lambda _2}-\frac{d_2 d_{18}}{1+\lambda _2}\right)H \mu ^2\notag\\ & +H^2 \mu \left(d_{11}-\frac{d_4 d_{18}}{1+\lambda _2}\right)+ O\left(\left|\mu + H|^4\right.\right). \end{aligned}\] Define \[\begin{aligned} l_1 =& \left(\frac{\partial ^2F_c}{\partial \mu \partial H} + \frac{1}{2}\frac{\partial F_c}{\partial H}\frac{\partial ^2F_c}{\partial \mu ^2}\right)_{(0,0)} = d_3 \neq 0,\\ l_2 =& \left(\frac{1}{6}\frac{\partial ^3F_c}{\partial \mu ^3} + \left(\frac{1}{2}\frac{\partial ^2F_c}{\partial \mu ^2}\right){}^2\right){}_{(0, 0)} = d_1{}^2+d_7+\frac{d_2 d_{16}}{1-\lambda _2} \neq 0. \end{aligned}\]
Theorem 4. [Period – Doubling Bifurcation] If \(1_1\neq0\) and \(1_2\neq2\), then system undergoes period – doubling bifurcation at the unique positive equilibrium point when parameters vary in small neighborhood of \(\Psi_{PD}\). Moreover, the period – two orbits that bifurcate from positive equilibrium are stable if \(l_2>0\) and unstable if \(l_2<0\).
Let \(M_{ NS}=\left\{(a, b, c,h, k,m, r,
\theta )\in \mathbb{R}_+^{7}:h =
h_{\Delta}\in\left(0,\left(\frac{4\Gamma
(1+\theta )}{r+x-\frac{a x y}{(m+x)^2}}\right)^{\frac{1}{\theta
}}\right)\right\}\) and h be the bifurcation parameter. Then
variation of parameters in small neighborhood of \(\Psi _{ NS}\) gives emergence of
Neimarck-Sacker bifurcation. Let \(h \in \Psi
_{ NS}\) and let H be the perturbation of h, where \(|H| < < < 1.\) The system can be
written as \[\left(
\begin{array}{c}
x \\
y \\
\end{array}
\right) \to \left(
\begin{array}{c}
x+\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}x\left(1- x – \frac{a y}{m
+ x}- \frac{k}{c+ x}\right) \\
y+\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}r y\left(1-\frac{b y}{m +
x}\right) \\
\end{array}
\right).\] As is done in the period- doubling subsection, the
system’s fixed point will be translated to (0,0) and we will get \[\left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) \to \left(
\begin{array}{c}
X+\frac{(h+H)^{\theta } \left(X+\bar{x}\right)
\left(1-X-\bar{x}-\frac{k}{c+X+\bar{x}}-\frac{a
\left(Y+\bar{y}\right)}{m+X+\bar{x}}\right)}{\Gamma
[1+\theta ]} \\
Y+\frac{(h+H)^{\theta } r \left(Y+\bar{y}\right) \left(1-\frac{b
\left(Y+\bar{y}\right)}{m+X+\bar{x}}\right)}{\Gamma [1+\theta ]} \\
\end{array}
\right).\] If we define,
\(A_1 = \bar{x}
\left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^2}\right);\)
\(A_2 = -\frac{a
\bar{x}}{\left(m+\bar{x}\right)}\);
\(A_3= \frac{b r
\bar{y}^2}{\left(m+\bar{x}\right)^2};\)
\(A_4 = r \left(\frac{2 b
\bar{y}}{m+\bar{x}}-1\right);\)
\(b_1
=-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^2}+\bar{x}
\left(-\frac{k}{\left(c+\bar{x}\right)^3}-\frac{a
\bar{y}}{\left(m+\bar{x}\right)^3}\right);\)
\(b_2 = -\frac{a m}{\left(m+\bar{x}\right)^2}
;\)
\(b_3 = 0;\)
\(b_4 =
-\frac{k}{\left(c+\bar{x}\right)^3}-\frac{a
\bar{y}}{\left(m+\bar{x}\right)^3}+\bar{x}
\left(\frac{k}{\left(c+\bar{x}\right)^4}+\frac{a
\bar{y}}{\left(m+\bar{x}\right)^4}\right);\)
\(b_5= \frac{a m
}{\left(m+\bar{x}\right)^3};\)
\(b_6 = 0;\)
\(b_7 = 0;\)
\(b_8 =-\frac{y r}{(m+x)^2} ;\)
\(b_9 = \frac{2 r}{m+x} ;\)
\(b_{10} = -\frac{b r}{m+x} ;\)
\(b_{11} = \frac{r y}{(m+x)^3}
;\)
\(b_{12} = -\frac{2
r}{(m+x)^2}\);
\(b_{13} = \frac{b r}{(m+x)^2}\);
\(b_{14} = 0.\) Then we can write our
system as \[\left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) \to \left(
\begin{array}{cc}
1+\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}A_1 &
-\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}A_2 \\
\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}A_3 &
1-\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]} A_4 \\
\end{array}
\right) \left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) + \left(
\begin{array}{c}
f_{NS}(X, Y) \\
g_{NS}(X, Y) \\
\end{array}
\right)\] where,
\[\begin{aligned}
f_{ NS}(X, Y) =& \frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}b_1 X^2 +
\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}b_2 X Y + \frac{(h+H)^{\theta
}}{\Gamma [1+\theta ]}b_3 Y^2 + \frac{(h+H)^{\theta }}{\Gamma [1+\theta
]} b_4 X^3 + \frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}b_5 X^2Y +\\
&\frac{(h+H)^{\theta}}{\Gamma [1+\theta ]}b_6 X Y^2 +
\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}b_7 Y^3 +
O\left(\left|X+Y|^4\right.\right)
\end{aligned}\] and \[\begin{aligned}
g_{ NS}(X, Y) =&\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]} b_8 X^2 +
\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}b_9 X Y +\frac{(h+H)^{\theta
}}{\Gamma [1+\theta ]} b_{10} Y^{ 2} +\frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]} b_{11} X^3 +\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}
b_{12} X^2 Y\\
&+\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]} b_{13} X Y^2 +
\frac{(h+H)^{\theta
}}{\Gamma [1+\theta ]} b_{14} Y^3 + O\left(\left|X+Y|^4\right.\right).
\end{aligned}\]
Let the characteristic polynomial of the above matrix at \((0, 0)\) be \(p_{ NS}( \lambda )=\lambda^2 – P( H)\lambda + Q(H)\). Thus, \[P(H) = \left(c_{11} + c_{22}\right) = 2+\frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}\left(A_1-A_4\right)\] and \[\begin{aligned} Q(H) =& c_{11}c_{22} – c_{21}c_{12} = \frac{(h+H)^{2\theta }}{\Gamma [1+\theta ]^2}\left.( A_3A_2-A_1A_4\right) + \frac{(h+H)^{\theta }}{\Gamma [1+\theta ]}\left(A_1-A_4\right) + 1,\\ Q(0) =& \frac{h^{2\theta }}{\Gamma [1+\theta ]^2}\left.( A_3A_2-A_1A_4\right) + \frac{h^{\theta }}{\Gamma [1+\theta ]}\left(A_1-A_4\right) + 1. \end{aligned}\] Since, parameters \((a,b,c,h,k,m,r,\theta)\in M_{NS},\) therefore the roots of \(p_{ NS}(\lambda)\) are complex numbers \(\lambda_1\) and \(\lambda_2\) with \(\lambda_2 = \bar{\lambda }_1\) and \(\left|\lambda_1\right| = \left|\lambda _2\right| = 1.\) It follows that, \(\lambda _1,\lambda _2 = \frac{P(H)}{2}\pm \frac{i}{2}\sqrt{4Q(H) – P(H)^2}\) and \(Q(H) = 1\) for any \(H > 0\). Also, \(P(H) \in(-2, 2)\) and \(\left(\frac{d \left|\lambda _1\right|}{ dH}\right)_{H=0} = \left(\frac{d \left|\lambda _2\right|}{dH}\right)_{H=0} =\frac{h^{\theta -1}}{\Gamma [1+\theta ]}\theta \left(\frac{h^{\theta }}{\Gamma [1+\theta ]}\left(A_2A_3 – A_1A_4\right)+\frac{A_1 – A_4}{2}\right)\) Thus, \(\left(\frac{d \left|\lambda _1\right|}{d H}\right)_{H=0}=\left(\frac{d \left|\lambda _2\right|}{d H}\right)_{H=0} \neq 0\) if \(r \left(\frac{2 b \bar{y}}{m+\bar{x}}-1\right)-\bar{x} \left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a \bar{y}}{\left(m+\bar{x}\right)^2}\right)\neq0.\)
In order to ensure that the roots of the charatceristic polynomial do
not lie in the intersection of unit circle of co- ordinate axis when
\(H=0\), we need to check that\(\lambda _1^n\) and \(\lambda _2^n \neq1\), for all \(n = 1, 2, 3, 4\) at \(H = 0\). This is equivalent to checking
\(\tau (0) \neq -2, 0, 1, 2\). Since,
parameters \((a,b,c,h,k,m,r,\theta)\in
M_{NS}\), we already know that \(P(0)
\neq-2, 0, 2.\) Also if \(h
\neq\left(\frac{\Gamma [1+\theta ]}{A_4-A_1}\right)^{\frac{1}{\theta
}}\), then \(P(0) \neq 1\). To
convert the above system to the normal form of Neimark- Sacker, when
\(H = 0\), let \(R = \frac{P(0)}{2}\) and \(S = \frac{1}{2}\sqrt{4Q(0) – P(0)^2}\) We
use the following transformation, \[\left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right)= T\left(
\begin{array}{c}
\mu \\
\eta \\
\end{array}
\right) =\left(
\begin{array}{cc}
0 & 1 \\
S & R \\
\end{array}
\right)\left(
\begin{array}{c}
\mu \\
\eta \\
\end{array}
\right)\] where \(T = \left(
\begin{array}{cc}
0 & 1 \\
S & R \\
\end{array}
\right)\), whcih is an invertible matrix. Using \(T\) we can write \[\left(
\begin{array}{c}
\mu \\
\eta \\
\end{array}
\right)= \left(
\begin{array}{cc}
R & -S \\
S & R \\
\end{array}
\right)\left(
\begin{array}{c}
\mu \\
\eta \\
\end{array}
\right) + \left(
\begin{array}{c}
\tilde{f}_{ NS}(u, v) \\
\tilde{g}_{ NS}(u, v) \\
\end{array}
\right)\] where, \[\tilde{f}_{ NS}(u,
v) = e_1 u^2 + e_2 u v + e_3 v^2 + e_4 u^3 + e_5 u^2v + e_6 u v^2 + e_7
v^3 + O\left(\left|u + v|^4\right.\right)\] and, \[\tilde{g}_{ NS}(u, v) = f_{ NS}(u, v) = e_8 u^2 +
e_9 u v + e_{10} v^2 + e_{11} u^3 + e_{12} u^2v + e_{13} u v^2 + e_{14}
v^3 +
O\left(\left|u + v|^4\right.\right)\] and,
\(e_1 = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}\frac{1}{S}\left(b_8+S \left(b_9+S b_{10}\right)-R
\left(b_1+S \left(b_2+S b_3\right)\right)\right);\)
\(e_2 = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}\frac{R}{S}\left(b_9+2 S b_{10}-R \left(b_2+2 S
b_3\right)\right);\)
\(e_3 = \frac{(h+H)^{\theta }}{\Gamma[1+\theta
]}\frac{R^2}{S}\left(b_{10}-R b_3\right);\)
\(e_4 = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}\frac{1}{S}\left(b_{11}+S \left(b_{12}+S \left(b_{13}+S
b_{14}\right)\right)-R \left(b_4+S \left(b_5+S
\left(b_6+S b_7\right)\right)\right)\right);\)
\(e_5 = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}\frac{R}{S}\left(\left(b_{12}+S \left(2 b_{13}+3 S
b_{14}\right)\right)-R\left(b_5+S
\left(2 b_6+3 S b_7\right)\right)\right);\)
\(e_6 = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}\frac{R^2}{S}\left(b_{13}+3 S b_{14} – R\left(b_6+3 S
b_7\right)\right);\)
\(e_7 = \frac{(h+H)^{\theta
}}{\Gamma [1+\theta ]}\frac{R^3}{S}\left(b_{14}-R
b_7\right);\)
\(e_8 = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}\left(b_1+S \left(b_2+S b_3\right)\right);\)
\(e_9 = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}R b_2;\)
\(e_{10} = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}R^2b_3;\)
\(e_{11} = \frac{(h+H)^{\theta }}{\Gamma
[1+\theta ]}\left(b_4 + S \left(b_5 + S\left(b_6 + S
b_7\right)\right)\right);\)
\(e_{12} = \frac{(h+H)^{\theta}}{\Gamma
[1+\theta ]}R \left(b_5+S \left(2 b_6+3 S b_7\right)\right); e_{13} = 0;
e_{14}=0.\)
Let,
\(\varpi _{20} =
\frac{1}{8}\left(\frac{\partial^2}{\partial u^2}\left(\tilde{f}_{
NS}\right)-\frac{\partial ^2}{\partial v^2}\left(\tilde{f}_{
NS}\right)+2\frac{\partial^2}{\partial u\partial
v}\left(\tilde{g}_{NS}\right) + \iota \left(\frac{\partial ^2}{\partial
u^2}\left(\tilde{g}_{NS}\right)-\frac{\partial^2}{\partial
v^2}\left(\tilde{g}_{NS}\right)-2\frac{\partial ^2}{\partial u\partial
v}\left(\tilde{f}_{ NS}\right)\right)\right);\)
\(\varpi _{11} =
\frac{1}{4}\left(\frac{\partial^2}{\partial u^2}\left(\tilde{f}_{
NS}\right)-\frac{\partial ^2}{\partial v^2}\left(\tilde{f}_{NS}\right)
+ \iota \left(\frac{\partial^2}{\partial u^2}\left(\tilde{g}_{
NS}\right)-\frac{\partial ^2}{\partial v^2}\left(\tilde{g}_{
NS}\right)\right)\right);\)
\(\varpi _{02}
=\frac{1}{8}\left(\frac{\partial ^2}{\partial u^2}\left(\tilde{f}_{
NS}\right) – \frac{\partial ^2}{\partial v^2}\left(\tilde{f}_{
NS}\right)
– 2\frac{\partial ^2}{\partial u\partial v}\left(\tilde{g}_{ NS}\right)
+ \iota \left(\frac{\partial ^2}{\partial
u^2}\left(\tilde{g}_{NS}\right)
– \frac{\partial ^2}{\partial v^2}\left(\tilde{g}_{ NS}\right) +
2\frac{\partial ^2}{\partial u\partial
v}\left(\tilde{f}_{NS}\right)\right)\right);\)
\(\varpi _{21} =
\frac{1}{16}\left(\frac{\partial^3}{\partial u^3}\left(\tilde{f}_{
NS}\right)+\frac{\partial^3}{\partial u\partial v^2}\left(\tilde{f}_{
NS}\right)+\frac{\partial
^3}{\partial u^2\partial v}\left(\tilde{g}_{
NS}\right)+\frac{\partial^3}{\partial
v^3}\left(\tilde{g}_{NS}\right)+\iota \left(\frac{\partial
^3}{\partial u^3}\left(\tilde{g}_{NS}\right)+\frac{\partial^3}{\partial
u\partial v^2}\left(\tilde{g}_{NS}\right)\right.\right.\)
\(\;\;\;\;\;\;\;\left.\left.-\frac{\partial
^3}{\partial
u^2\partial v}\left(\tilde{f}_{NS}\right)-\frac{\partial^3}{\partial
v^3}\left(\tilde{f}_{NS}\right)\right)\right).\)
In order to undergo Neimark-Sacker bifurcation for (48), we require that
the following discriminatory quantity is not zero. \[\mho=\left(- Re\left[\varpi _{20}\varpi
_{11}\frac{\left(1 – 2 \lambda _1\right)\lambda _{2}^2}{1 – \lambda
_1}\right] – \frac{1}{2}|\varpi
_{11}|^2 – \left|\varpi _{02}|^2 + Re\left[\varpi _{21}\lambda
_2\right]\right.\right)_{H = 0}\neq 0.\]
Theorem 5. [Neimark-Sacker Bifurcation] Suppose \((a,b,c,h,k,m,r,\theta )\in M_{NS}, r \left(\frac{2 b \bar{y}}{m+\bar{x}}-1\right)-\bar{x} \left(-1+\frac{k}{\left(c+\bar{x}\right)^2}+\frac{a \bar{y}}{\left(m+\bar{x}\right)^2}\right) \neq 0, h \neq \left(\frac{\Gamma [1+\theta ]}{A_4-A_1}\right)^{\frac{1}{\theta }}\) and \(\mho \neq 0.\) Then the model (1) undergoes Neimark-Sacker bifurcation at the equilibrium point \(\left(\bar{x}, \bar{y}\right)\) provided that parameter h changes in the small neighborhood of \(h_{\Delta }\). Moreover, if \(\mho <0 ( resp.,\mho >0),\) then an attracting ( resp., repelling) invariant closed curve bifurcate from the fixed point \(\left(\bar{x}, \bar{y}\right)\) for \(h>h_{\Delta } \left( resp.,h<h_{\Delta }\right)\).
In this section, we utilize Mathematica to perform numerical simulations that validate the analytical results presented in sections §2.5, §3.1, and §3.2. The simulations not only confirm the analytical findings but also provide further insights into the local stability of the positive interior fixed point.
It is well-known that slight variations in the parameter values can result in significant changes in the system’s trajectories, making its dynamics more intricate. To demonstrate this phenomenon, we select specific parameter values \(\left(\alpha, \beta, \theta, h\right)\) and present multiple numerical examples that illustrate the occurrence of period-doubling and Neimark-Sacker bifurcations in the system described by (1). Additionally, we provide an example that demonstrates the occurrence of only the Neimark-Sacker bifurcation in the same system.
To visualize the bifurcations, we utilize phase portraits and bifurcation diagrams. These numerical examples serve to confirm the validity of Theorems 4 and 5.
In summary, the numerical simulations presented in this section provide further evidence of the complex dynamics exhibited by the discrete fractional modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting. These results complement the analytical findings and enhance our understanding of the behavior of real-world predator-prey systems.
Example 1. We consider the system (1) with the parameters \(\left(a, b, k, m, c, r, h, \theta\right)\) \(=\) \(\left(0.01, 0.6, 0.2, 0.4, 0.1, 1.9, 0.8843446, 0.5\right)\) and initial values \((x_0, y_0) = \left(0.3, 0.4\right)\). The local stability of the interior fixed point is analyzed by investigating the eigenvalues of the Jacobian matrix evaluated at the fixed point. The Jacobian matrix is, \[\left( \begin{array}{cc} 0.439471 & -0.00691164 \\ 3.36022 & -1.01613 \\ \end{array} \right)\,.\] The eigenvalues of the Jacobian matrix corresponding to the fixed point \(\left(0.747285, 1.91214\right)\) are \(\lambda_1 = -1\) and \(\lambda_2 = 0.423337\). Figure 1(a) displays the phase portraits of map (4) for \(h=0.83\), which reveals that the fixed point is stable for \(h < h_0\). A period-doubling bifurcation occurs around \(h_0\), as evidenced by the appearance of another stable period-doubling bifurcation at approximately \(h = 0.85\). At approximately \(h = 1.955\), there are eight paths of the system. These observations are further corroborated by the bifurcation diagrams in Figure 1(b). The maximum Lyapunov Exponent for the system with initial conditions \((x_0, y_0) = (0.3, 0.4)\) and \(h \in [0.85, 1.58]\) is shown in Figure 1(c).
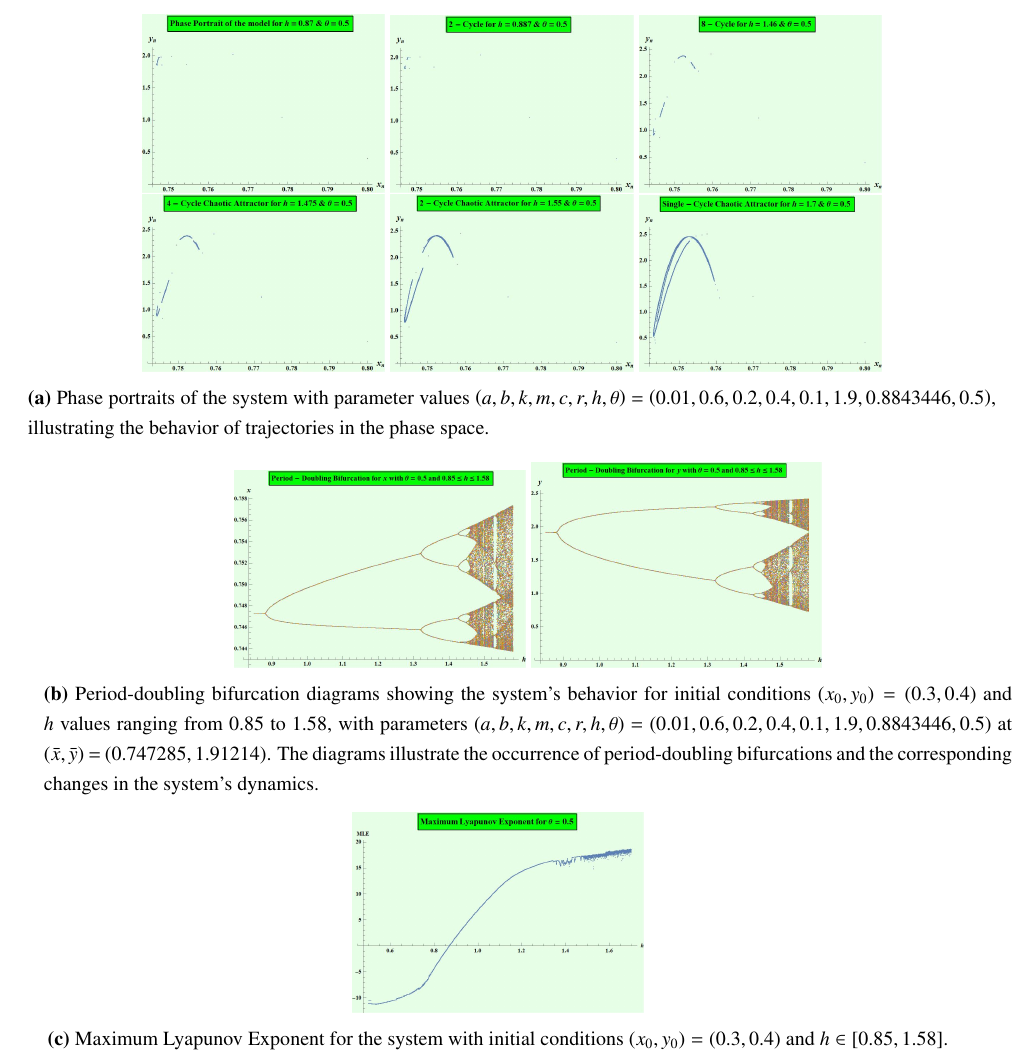
Example 2. Let \(\left(a, b, k, m, c, r, h, \theta\right)\) \(=\) \(\left(0.01, 0.6, 0.2, 0.4, 0.1, 1.9, 0.8497418, 0.3\right)\), \(h\) be in the interval \([0.8, 2.01]\), and consider the initial values \((x_0, y_0) = \left(0.3, 0.4\right)\). The interior fixed point exhibits different stability behaviors depending on the value of \(h\). Specifically, it is locally asymptotically stable for \(h \in (0, 0.8497418)\), locally unstable for \(h \in (53.65958, \infty)\), and a saddle for \(h \in (0.8497418, 53.65958)\). The corresponding Jacobian matrix is given by, \[\left( \begin{array}{cc} 0.439471 & -0.00691164 \\ 3.36022 & -1.01613 \\ \end{array} \right)\,.\] The eigenvalues corresponding to the system are \(\lambda_1 = -1\) and \(\lambda_2 = 0.423337\). The phase portrait displayed in Figure 2(a) indicates that the fixed point \(\left(0.747285, 1.91214\right)\) of map (4) is stable for values of \(h\) less than \(h_0\), where \(h_0 \approx 0.887\), and the system undergoes a period-doubling bifurcation around \(h_0\). Additionally, another stable period-doubling bifurcation is observed at approximately \(h = 0.887\), leading to the emergence of 8 system paths around \(h = 1.46\). These observations are consistent with the bifurcation diagrams depicted in Figure 2(a).
The aforementioned results illustrate the sensitivity of the system’s behavior to slight variations in the parameter values, leading to the occurrence of period-doubling and bifurcations. By employing phase portraits and bifurcation diagrams, we can visualize these complex dynamical behaviors and verify the validity of Theorems 4 and 5. Overall, these numerical simulations serve to further our understanding of the discrete fractional modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting and its behavior in real-world predator-prey systems.
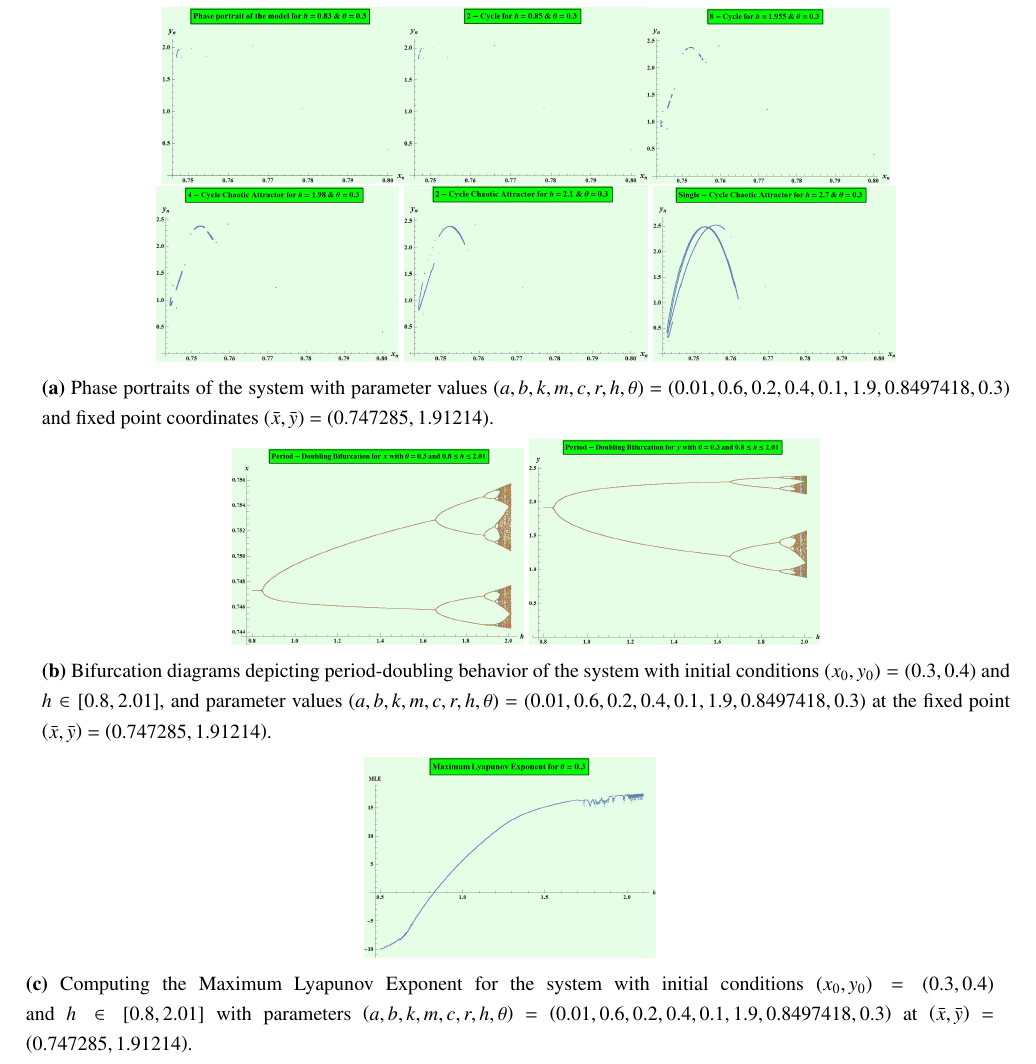
Example 3. Consider the values of the parameters \(\left(a, b, k, m, c, r, h, \theta\right)\) \(=\) \(\left(0.05, 2.3, 0.001, 0.05, 0.5, 1.275, 2.5196, 0.5\right)\), the initial value \((x_0, y_0) = \left(0.9, 0.35\right)\), and \(h\) in the interval \([2.47, 3.22]\). At the value \(h_0 = 2.5196\), the Jacobian matrix is given by: \[\left( \begin{array}{cc} -0.713118 & -0.085198 \\ 0.992899 & -1.28367 \\ \end{array} \right)\,.\] The system with \(\left(a, b, k, m, c, r, h, \theta\right)\) \(=\) \(\left(0.05, 2.3, 0.001, 0.05, 0.5, 1.275, 2.5196, 0.5\right)\) and initial value \((x_0, y_0) = \left(0.9, 0.35\right)\) undergoes a Neimark-Sacker bifurcation at \(\left(\bar{x}, \bar{y}\right)\) \(=\) \(\left(0.9775840891319717, 0.44677569092694425\right)\) when \(h\) is increased beyond the threshold value of \(2.5196\). At the bifurcation point, both eigenvalues are on the unit circle, with \(\lambda_1 = -0.99839308 + 0.05666797\iota\) and \(\lambda_2 = -0.99839308 – 0.05666797\iota\). Additionally, \(tr\left(J\right) = -1.99679\) and \(\left\vert J\right\vert = 1\) at \(h = h_0\). The fixed point exhibits an attracting invariant closed curve with rough edges as can be seen in Figure 3(a). The parameters \(\left(\frac{d\left|\lambda_{1}\right|}{d \mathcal{H}}\right){\mathcal{H}=0} = \left(\frac{d\left|\lambda{2}\right|}{d\mathcal{H}}\right)_{\mathcal{H}=0} = 2.23145 \neq 0\) and \(\mho = -1.88841 \times 10^{18} \neq 0\) confirm the occurrence of the Neimark-Sacker bifurcation.
As shown in Figure 3(b), as \(h\) increases from \(2.4\), the stable fixed point changes from a stable spiral point to an attracting invariant closed curve with rough edges. At \(h = 2.54\), the spiral and edges can be seen, and as \(h\) is further increased, the rough edges disappear, leaving only the attracting invariant closed curve.
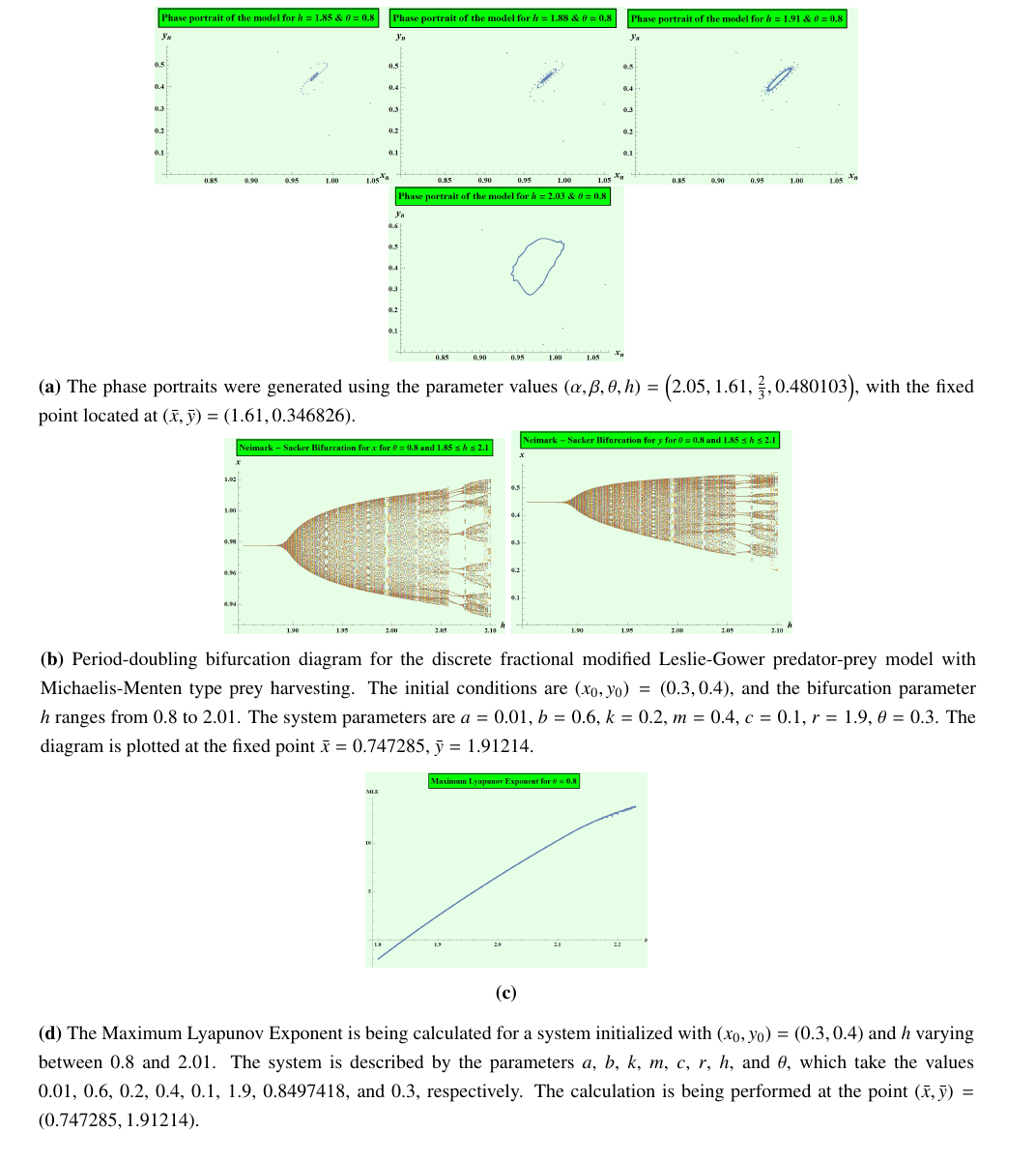
Example 4. Take \(\left(a, b, k, m, c, r, h, \theta\right)\) \(=\) \(\left(0.05, 2.3, 0.001, 0.05, 0.5, 1.275, 1.895895, 0.8\right)\), \(h\) ranging from 1.85 to 2.1, and the initial condition \((x_0, y_0) = \left(0.9, 0.35\right)\). In Figure 4, it can be observed that for \(h > 1.895895\), an attracting invariant closed curve emerges from the fixed point.
As shown in Figure 4(a), the stable fixed point becomes unstable beyond the threshold value \(1.895895\) due to the Neimark-Sacker bifurcation. At \(h = 1.85\), the fixed point can be identified as a stable spiral point. With increasing \(h\), the stable spiral grows in size. As \(h\) approaches the threshold value \(h_0 = 1.895895\), the spiral transforms into an attracting invariant closed curve with rough edges because of the Neimark-Sacker bifurcation. For \(h = 1.91\), the spiral and edges are plotted. When \(h\) surpasses \(h_0\), all the rough edges disappear, leaving behind only the attracting invariant closed curve.
In this paper, we have investigated the dynamics of the discrete fractional modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting with a piece-wise constant argument. Our study has resulted in several significant findings that can be extended and applied to real-world predator-prey systems.
Firstly, we have shown that the system has a unique solution, and the stability of fixed points and their topological properties have been discussed. Furthermore, we have demonstrated that the system exhibits period-doubling and Neimark-Sacker bifurcations for certain values of the chosen bifurcation parameter. We have discussed and proved the bifurcation scenarios for the unique interior fixed point using the center limit theorem. Additionally, our numerical examples have depicted the period-doubling bifurcation for different fractional orders, highlighting the importance of considering fractional order models in predator-prey studies.
Our results have important implications for the understanding and management of real-world predator-prey systems. By providing insight into the dynamics of the modified Leslie-Gower predator-prey model, our findings can inform the development of management strategies for these systems. Moreover, our study highlights the need to consider fractional order models, as they can exhibit complex dynamics not seen in integer-order models.
Overall, our study contributes to the body of knowledge on predator-prey dynamics and provides a foundation for further research in this area. By continuing to investigate the dynamics of predator-prey systems, we can gain a better understanding of these complex ecological interactions and develop more effective management strategies to ensure their sustainability.
some potential future directions related to the paper are; 1) Investigating the effect of different forms of prey harvesting on the behavior of the modified Leslie-Gower predator-prey model, such as continuous or time-dependent harvesting. 2) Studying the impact of different forms of functional response, such as Holling type II or III, on the dynamics of the model. 3) Exploring the behavior of the model in a spatially explicit setting, where the predators and prey can move and interact in a heterogeneous environment. 4) Extending the model to include additional trophic levels and studying the effects of top-down and bottom-up regulation on the ecosystem dynamics. 5) Investigating the effects of stochasticity on the model, such as incorporating random fluctuations in population sizes or environmental parameters. 6) Developing control strategies to manage or mitigate the negative impacts of predator-prey interactions on natural ecosystems or agricultural systems. 7) Examining the impact of external factors such as climate change or habitat destruction on the predator-prey dynamics and exploring ways to mitigate their negative effects.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.