A graph G(V, E) is Γ-harmonious when there is an injection f from V to an Abelian group Γ such that the induced edge labels defined as w(xy) = f(x) + f(y) form a bijection from E to Γ. We study Γ-harmonious labelings of several cycles-related classes of graphs, including Dutch windmills, generalized prisms, generalized closed and open webs, and superwheels.
Harmonious graphs have been extensively studied since 1980, when Graham and Sloane [1]first defined the notion.
A graph \(G=(V,E)\) with \(q\) edges is harmonious if there exists an injection \(f\) from the set of vertices of \(G\) to the additive group \({Z}_q\), \(f: V\to{Z}_q\) such that the induced edge labels \(w(e)\) of all edges, defined as \(w(xy)=(f(x)+f(y))\mod q\), are all distinct.
That is, the induced function \(w:E\to{Z}_q\) is a bijection. When \(G\) is a tree, exactly one vertex label is repeated. Graham and Sloane proved that almost all graphs are not harmonious. They also proved that if a harmonious graph has an even number of edges \(q\) and the degree of every vertex is divisible by \(2k\) then \(q\) is divisible by \(2k+1\). Liu and Zhang [2]generalized this condition and also proved that there is no forbidden subgraph condition for harmonious graphs, that is, that every graph is a subgraph of a harmonious graph.
In this paper, we study the concept of \(\Gamma\)-harmonious graphs by extending the notion of harmonious graphs to any Abelian group \(\Gamma\). We say that a graph \(G\) with \(q\) edges is \(\Gamma\)-harmonious for a given Abelian group \(\Gamma\) of order \(q\) if there exists an injection \(f: V\to\Gamma\) such that the induced labels \(w(e)\) of all edges, defined as \(w(xy)=f(x)+f(y)\) (where the addition is performed in \(\Gamma\)), are again all distinct. In other words, the induced function \(w:E\to\Gamma\) is a bijection. This notion was introduced by Montgomery, Pokrovskiy and Sudakov in [3], but their results were all dealing just with cyclic groups. We are not aware of any results for non-cyclic groups whatsoever.
We will present several classes of cycles-related graphs that are \(\Gamma\)-harmonious for various Abelian groups \(\Gamma\). All groups in this paper are finite.
We will use \(A, H\) for subgroups, and the group operation will be the usual component-wise addition. A coset determined by a subgroup \(A\) of \(\Gamma\) and a coset representative \(\alpha\) will then be denoted by \(\alpha+A\). A cyclic subgroup of \(Z_n\) generated by an element \(a\) will be denoted by \(\langle a\rangle_n\) or simply \(\langle a\rangle\) if no confusion can arise.
First we repeat the formal definition of \(\Gamma\)-harmonious graphs.
Definition 1. Let \(G=(V,E)\) be a graph with \(q\) edges and \(\Gamma\) an Abelian group of order \(q\). We say that \(G\) is \(\Gamma\)-harmonious if there exists an injection \(f: V\to\Gamma\) (called \(\Gamma\)-harmonious labeling) with the property that the induced labels \(w(e)\) of all edges, defined as \(w(xy)=f(x)+f(y)\) (where the addition is performed in \(\Gamma\)), are all distinct. In other words, the induced function \(w:E\to\Gamma\) is a bijection.
When \(\Gamma=Z_q\), then a \(Z_q\)-harmonious graph is simply called harmonious.
Definition 2. A graph \(G\) with \(q\) edges is strongly \(\Gamma\)-harmonious if it is \(\Gamma\)-harmonious for all Abelian groups of order \(q\).
Now we present definitions of the classes of graphs studied in the following sections.
Definition 3. The wheel graph \(W_n\) arises from the cycle \(C_n\) by adding a single vertex and joining it by an edge to every vertex of the cycle.
The wheel graph is often described as \(C_n + K_1\).
Definition 4. The superwheel \(SW_{k,n}\) is a graph arising from the cycle \(C_n\) by adding \(k\) vertices not adjacent to each other but adjacent to every vertex in \(C_n\).
The number of edges in \(SW_{k,n}\) is \((k+1)n\). It can be also described as \(C_n + kK_1\) or \(C_n + \overline{K_k}\). When \(k=1\), \(SW_{1,n}\) is just the wheel \(W_n\).
Definition 5. The Dutch windmill graph \(D_n^m\) is a graph consisting of \(m\) copies of \(C_n\) with a common vertex, called the central vertex. The \(n\)-cycles in \(D_n^m\) are also called blades.
The number of edges of \(D_n^m\) is \(nm\). When \(m=1\), \(D_n^1\) is a cycle; thus, in our examination, \(m>1\). For \(n=3\), the graph \(D^m_3\) is also called the friendship graph.
Definition 6. The generalized prism \(Y_{m,n}\) is the Cartesian product of the path \(P_m\) and the cycle \(C_n\).
The number of edges in \(Y_{m,n}\) is \((2m-1)n\). When \(m=2\), we obtain the usual prism. The cycle \(C_n\) can also be seen as the degenerate generalized prism \(Y_{1,n}\).
Definition 7. The generalized closed web \(CW_{m,n}\) is a graph arising from the generalized prism \(Y_{m,n}\) by adding a new vertex and joining it by an edge to every vertex of degree three of the top cycle of \(Y_{m,n}\).
The number of edges in \(CW_{m,n}\) is \(2mn\). The closed web \(CW_{2,n}\) is sometimes also called the closed helm (see below). The wheel \(W_n\) is \(CW_{1,n}\).
Definition 8. The generalized open web \(OW_{m,n}\) is a graph arising from the generalized closed web \(CW_{m,n}\) by removing the edges of the bottom cycle \(C_n\).
The number of edges in \(OW_{m,n}\) is \((2m-1)n\). The generalized open web \(OW_{m,n}\) is sometimes called just the generalized web. The open web \(OW_{2,n}\) is better known as the helm graph. The usual web graph is then \(OW_{3,n}\).
For the sake of completeness, we first state some well known group theory results, which we will use later, starting with The Fundamental Theorem of Finite Abelian Groups. Although the reader is probably familiar with the theorems, we include them primarily because of introducing notation that will be used throughout the paper.
Theorem 1 (The Fundamental Theorem of Finite Abelian Groups). Let \(\Gamma\) be an Abelian group of order \(n=p^{s_1}_1 p^{s_2}_2\dots p^{s_k}_k\), where \(k\geq1\), \(p_1,p_2,\dots,p_k\) are primes, not necessarily distinct, and \(s_1,s_2,\dots,s_k\) positive integers.
Then \(\Gamma\) is isomorphic to \(Z_{p^{s_1}_1}\oplus Z_{p^{s_2}_2}\oplus\dots\oplus Z_{p^{s_k}_k}\) and if we moreover require that for every \(i=1,2,\dots,k-1\) we have \(p_i\leq p_{i+1}\) and if \(p_i=p_{i+1}\), then \(s_i\leq s_{i+1}\), then the expression determined by the \(k\)-tuple \((p^{s_1}_1,p^{s_2}_2,\dots,p^{s_k}_k)\) is unique and we call it the canonical form of the group \(\Gamma\).
Sometimes it is useful to express an Abelian group in a different way.
Theorem 2. Let \(\Gamma=Z_{p^{s_1}_1}\oplus Z_{p^{s_2}_2}\oplus\dots\oplus Z_{p^{s_k}_k}\) of order \(n\) be as in Theorem 1. Then it can be written in a unique way in nested form as \(\Gamma=Z_{n_1}\oplus Z_{n_2}\oplus\dots\oplus Z_{n_t}\), where \(n_t\geq2, \ n= n_1 n_2\dots n_t,\) and \(n_{i+1}\mid n_i\) for \(i=1,2,\dots,t-1\).
Another well known theorem is the following.
Theorem 3. An Abelian group \(\Gamma%(p^{s_1}_1,p^{s_2}_2,\dots,p^{s_k}_k) =Z_{p^{s_1}_1}\oplus Z_{p^{s_2}_2}\oplus\dots\oplus Z_{p^{s_k}_k}\) is cyclic if and only if all primes \(p_i\), \(i=1,2,\dots,k\) are distinct.
The following observation will be useful.
Observation 4. Let \(\Gamma=Z_{n_1}\oplus Z_{n_2}\oplus\dots\oplus Z_{n_t}\) of order \(n\) satisfy conclusion of Theorem 2 and \(H\) be its cyclic subgroup of order \(m\). Then \(m\mid n_1\) and \(Z_{n_1}\) has a cyclic subgroup of order \(m\).
Proof. Let \(Z_{q^{z_1}_1}\oplus Z_{q^{z_2}_2}\oplus\dots\oplus Z_{q^{z_r}_r}\) be the canonical form of \(Z_{n_1}\). Then by Theorem 3 \(q_1,q_2,\dots,q_r\) are all distinct. Moreover, \(q_1,q_2,\dots,q_r\) are all primes in the multiset \(\{p_1,p_2,\dots,p_k\}\) defining the canonical form of \(\Gamma\). For if not, then there is \(p_i\) which appears in the canonical form of some \(Z_{n_j}, j>1\) but not in \(\{q_1,q_2,\dots,q_r\}\). But then \(n_j\) does not divide \(n_1\), which contradicts Theorem 2. Therefore, we can write \(H\) as \(Z_{q^{u_1}_1}\oplus Z_{q^{u_2}_2}\oplus\dots\oplus Z_{q^{u_r}_r}\), where we allow each \(u_i\) to be a non-negative integer.
For the same reason as above we must have \(u_i\leq z_i\) for every \(i=1,2,\dots,r\), since otherwise \(q^{u_i}_i\) appears in the canonical form of some \(Z_{n_j}, j>1\) and \(n_j\nmid n_1\), a contradiction. ◻
Another well-known result will be useful.
Theorem 5. Let \(\Gamma\) be a finite Abelian group. Then
if \(H\) is a subgroup of \(\Gamma\), then the quotient group \(\Gamma/H\) is isomorphic to some subgroup \(K\) of \(\Gamma\), and conversely,
if \(K\) is a subgroup of \(\Gamma\), then there exists a subgroup \(H\) such that \(K\cap H=\{e\}\) and the quotient group \(\Gamma/H\) is isomorphic to \(K\).
The main building block we will be using in our constructions is a theorem that follows as a direct corollary form a group theory result proved by Beals, Gallian, Headly and Jungreis [4]. They studied harmonious groups.
Definition 9. A finite group \(\Gamma\) of order \(n\) is harmonious if the elements can be ordered \((g_1,g_2,\dots,g_n)\) so that the set of element products \(\{g_1g_2,g_2g_3,\dots,g_{n-1}g_n,g_ng_1\}\) is equal to the set of all elements of \(\Gamma\). The ordered list \((g_1,g_2,\dots,g_n)\) is called the harmonious sequence of \(\Gamma\).
They proved the following characterization of harmonious groups.
Theorem 6 (Beals et al. [4]). If \(\Gamma\) is a finite, non-trivial Abelian group, then \(\Gamma\) is harmonious if and only \(\Gamma\) has a non-cyclic or trivial Sylow \(2\)-subgroup and \(\Gamma\) is not an elementary \(2\)-group.
In other words, all non-trivial Abelian groups of odd order are harmonious, and a harmonious group of even order must contain a subgroup isomorphic to \(Z_{2}\oplus Z_{2}\) but cannot be equal to \(Z_2\oplus Z_2\oplus\dots\oplus Z_2\). That is, it must contain a subgroup isomorphic to \(Z_2\oplus Z_{2s}\) where \(s\geq2\).
An immediate consequence of Theorem 6 is a result on \(\Gamma\)-harmonious labeling of cycles, which we state in the next section.
The first result on cycle-related harmonious graphs was proved by Graham and Sloane [1]. Note that “harmonious” here means “\(Z_n\)-harmonious.”
Theorem 7 (Graham and Sloane [1]). The cycle \(C_n\) with \(n\geq 3\) is harmonious if and only if \(n\) is odd.
A more general theorem is a direct consequence of Theorem 6. Although it is technically speaking a new result, as it was not formally stated and proved in [4], we state it here because we believe that the authors were aware of it.
Theorem 8. The cycle \(C_n\) is \(\Gamma\)-harmonious if and only if \(\Gamma\) is of order \(n\), and
\(n\) is odd, or
\(n\) is even and \(\Gamma\) has a subgroup isomorphic to \(Z_2\oplus Z_{2s}\) where \(s\geq2\).
Proof. This follows directly from Theorem 6. Label the vertices consecutively with the elements of \(\Gamma\) in their harmonious sequence order. ◻
Graham and Sloane [1]further proved the following result on wheel graphs.
Theorem 9 (Graham and Sloane [1]). All wheels \(W_n\) are harmonious.
We generalize their result in the Section 7. We prove that odd wheels \(W_{2k+1}\) are strongly \(\Gamma\)-harmonious, and even wheels are \(\Gamma\)-harmonious for certain groups \(\Gamma\).
Gallian [5]cites [6]which has the following two results on superwheel graphs.
Theorem 10 (Gnanajothi [6]). The superwheel graph \(S_{k,n}\) is harmonious if \(n\) is odd and \(k=2\).
Theorem 11 (Gnanajothi [6]). The superwheel graph \(S_{k,n}\) is not harmonious if \(n \equiv 2,4,6 \mod 8\) and \(k=2\).
We will show that all odd superwheel graphs are strongly \(\Gamma\)-harmonious and even superwheel graphs are \(\Gamma\)-harmonious for some groups.
Graham and Sloane [1] also established the following result on Dutch windmill graphs.
Theorem 12 (Graham and Sloane [1]). The Dutch windmill graph \(D_3^m\) is harmonious if and only if \(m\not \equiv 2 \mod 4\).
We will prove that when both \(m\) and \(n\) are odd, \(D_n^m\) is strongly \(\Gamma\)-harmonious. Moreover, we will show for \(m\) odd and \(n\) even, \(D_n^m\) is \(\Gamma\)-harmonious for certain groups.
Also, Graham and Sloane [1]proved the following result on generalized prisms.
Theorem 13 (Graham and Sloane [1]). The generalized prism \(Y_{m,n}\) is harmonious whenever \(n\) is odd and \(m\geq 2\).
Later, Gallian, Prout and Winters [7]showed the following result on even prisms.
Theorem 14 (Gallian et al. [7]). The prism \(Y_{2,n}\) is harmonious except when \(n=4\).
Jungreis and Reid [8]showed the following results on type harmonious prisms. \(Y_{2m,4n}\) and \(Y_{2m+1,4m}\)
Theorem 15 (Jungreis and Reid [8]). The generalized prism \(Y_{m,n}\) is harmonious if:
\(m=2k\) and \(n=4l\) except when \((k,l)=(1,1)\)
\(m=2k+1\) and \(n=4l\)
\(m=2k\) and \(n=4l+2\)
\(n=2l+1\)
We prove results on generalized prisms showing \(Y_{m,n}\) is \(\Gamma\)-harmonious for some \(\Gamma\).
Seoud and Youssef [9]proved the following two results on open webs (or helm graphs) \(OW_{2,n}\) and closed webs (or closed helms) \(CW_{2,n}\).
Theorem 16 (Seoud and Youssef [9]). The open web \(OW_{2,n}\) is harmonious for all \(n\geq 3\).
Theorem 17 (Seoud and Youssef [9]). The closed web \(CW_{2,n}\) is harmonious for all odd \(n\geq 3\).
In [5], Gallian cites [6]which states the following result on open webs \(OW_{3,n}\).
Theorem 18 (Gnanajothi [6]). The open web \(OW_{3,n}\) is harmonious when \(n\) is odd and \(n\geq 3\).
We will generalize results on \(OW(m,n)\) and \(CW(m,n)\) by showing that they are \(\Gamma\)-harmonious for certain \(\Gamma\).
The superwheel \(SW_{k,n}\) is a graph with a cycle of length \(C_n\) and has \(k\) vertices not adjacent to each other but all adjacent to every vertex in \(C_n\). The number of edges of \(SW_{k,n}\) is \(n(k+1)\). When \(k=1\), then \(SW_{k,n}\) is the wheel \(W_n\).
Theorem 19. The superwheel \(SW_{k,n}\) is \(\Gamma\)-harmonious with \(\Gamma\) of order \(n(k+1)\) if there exists a subgroup \(H\) of order \(n\) that satisfies conditions in Theorem 8.
Proof. Let \(v_1,v_2,\dots,v_n\) be the vertices of the \(C_n\) in \(SW_{k,n}\) and \(u_1,u_2,\dots,u_k\) be the the vertices in its center. For \(1\leq j\leq k\), let \(E_j=\{u_jv_i|v_i\in V(C_n)\}\).
Assume \(H\) is a subgroup of order \(n\) that satisfies Theorem 8. Then we can find a \(\Gamma\)-harmonious labeling of \(C_n\) with \(H\). Let \((h_1,h_2,\dots,h_n)\) be a \(H\)-harmonious labeling of \(C_n\), where for \(1\leq i\leq n, v_i\) is labeled with the element \(h_i\in H\). We can write \(\Gamma\) as the following disjoint union, \(\Gamma= H\cup g_1+H\cup g_2+H\cup\dots\cup g_k+H\) for \(g_1,g_2,\dots,g_k\) in \(G- H\). For \(1\leq j\leq k\), label the central vertex \(u_j\) with \(g_j\). Thus, for a fixed \(j\), the edge \(u_jv_i\) in \(E_j\) would be labeled with \(g_j+h_i\), which is an element of \(g_j +H\).
Since for a fixed \(j\), each \(g_j+h_i\) is distinct, there would be no repetition among the edge labels of the edges in \(E_j\). Hence, the edges of \(C_n\) are labeled with elements of \(H\) and the edges of \(E_j\) are labeled with those of \(g_j+H\). Since the cosets are disjoint, there would be no repetition in the edge labels across all edges of \(SW_{k,n}\) Thus, we have our \(\Gamma\)-harmonious labeling of \(SW_{k,n}\). ◻
We illustrate the method by two examples.
Example 1. A \(Z_{10}\oplus Z_2\) labeling of the superwheel \(SW_{3,5}\).
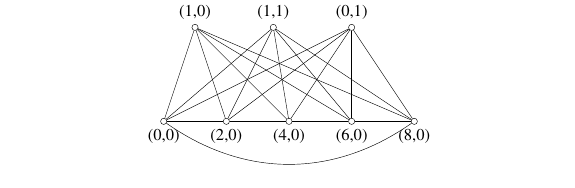
Example 2. A \(Z_4\oplus Z_2\oplus Z_4\) labeling of the superwheel \(SW_{3,8}\).
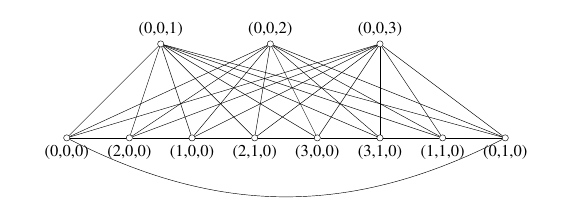
The Dutch windmill graph \(D_n^m\) is a graph consisting of \(m\) copies of \(C_n\) with a common vertex, called the central vertex. The \(n\)-cycles in \(D_n^m\) are also called blades. Therefore, the number of edges of \(D_n^m\) is \(nm\). When \(m=1\), \(D_n^m\) is a cycle; thus, in our examination, \(m>1\).
We know that \(m\mid|\Gamma|\). Therefore, there must be a subgroup \(H\) of order \(m\) and index \(n\). Because \(\Gamma\) is Abelian, \(H\) is normal. Therefore, \(K=\Gamma/H\) is a quotient group. Denote the coset representatives of \(K\) by \(\gamma_{0}=\mathbf{0}, \gamma_{1},\gamma_{2},\dots,\gamma_{n-1}\), where \(\mathbf{0}\) is the identity element of \(\Gamma\) (and thus of \(H\) as well). Since there are \(m\) copies of \(C_n\), we can denote each \(C_n\) as \(C^j\) where \(0\leq j\leq m-1\). Let \(u\) be the central vertex. In each \(C^j\), we denote other vertices by \(v^j_i\) for \(i=1,2,\dots,{n-1}\) such that the the edges in \(C^j\) are \(e^j_0=uv^j_1, e^j_i=v^j_i v^j_{i+1}\) for \(i=1,2,\dots, n-2\), and \(e^j_{n-1}=v^j_{n-1}u\).
Before we start constructing the vertex labeling of \(D^m_n\) with \(\Gamma\), it is convenient to prove the following observation. We will show that there exists a valid labeling of \(C^j\) with \(K\). The coset representatives of the elements of \(K\) in the vertex labeling of \(v_i^j\) in the \(K\)-harmonious labeling of \(C^j\) will be later used in the construction of a valid labeling of \(D_n^m\) with \(\Gamma\).
Observation 20. If \(n\) is odd then each \(C^j\) has a \(K\)-harmonious labeling where \(u\) is labeled with \(H\).
Proof. Since \(K\) is an Abelian group of order \(n\), there exists a \(K\)-harmonious labeling of each \(C^j\). Thus, we can find a \(K\)-harmonious labeling \(g\) of \(C^j\) such that \(u\) is labeled with \(H\) and \(v_i^j\) is labeled with \(g(v^j_i)=\gamma_i+H\) for \(\gamma_i+H\in K=\Gamma/H\), where \(\gamma_{i}\notin H\). The induced edge label of edge \(e\) is denoted by \(w_g(e)\). Notice that while we are labeling the cycle with cosets, the labeling is well-defined since they are elements of the group \(K\). Notice that we label the cycles with the cosets; this labeling is well-defined because they are elements of \(K\), which is a group.
Let \(\tilde {\gamma}_0+H=\gamma_1+H\) and \(\tilde {\gamma}_{n-1}+H=\gamma_{n-1}+H\) and for \(1\leq i\leq n-2\), \(\tilde {\gamma}_{i}+H=\gamma_i+\gamma_{i+1}+H\). In this scheme, \(w(e_i^j)=\tilde {\gamma}_i+H\). ◻
Let us look at a specific example how we would use this lemma to construct a vertex labeling of \(D_5^3\) with \(\Gamma={Z}_5\oplus {Z}_3\) that would induce a \(\Gamma\)-harmonious labeling. We realize that the group \(Z_5 \oplus Z_3\) is in fact isomorphic to \(Z_{15}\), but we are using this example to illustrate how the method works for a group of type \(Z_a \oplus Z_b\). It is independent on whether or not the numbers \(a\) and \(b\) are relatively prime.
Example 3. \(\Gamma\)-harmonious labeling of \(D_5^3\) with \(\Gamma={Z}_5\oplus {Z}_3\cong Z_{15}\).
Here, we have, \(H=\{0\}\oplus{Z}_3\) and \(K=\{H,(1,0)+H,(2,0)+H,(3,0)+H,(4,0)+H\}\). In Figure 3 (a), we have a \(K\)-harmonious labeling for each \(C^j\), where \(u\) is labeled with \(H\), and in each \(C^j\), \(v_i^j\) is labeled with \((i,0)+H\).
In Figure 3(b), \(u\) is labeled with \((0,0)\). We have chosen a distinct element of \(\{0\}\oplus {Z}_3\) for each \(C^j\) specifically, \(h_1=(0,0)\) for \(C^1\), \(h_2=(0,1)\) for \(C^2\), and \(h_3=(0,2)\) for \(C^3\). We labeled the vertices \(v_i^1\) with \((1,0)+(0,0),(2,0)+(0,0),(3,0)+(0,0),(4,0)+(0,0)\). Similarly, we labeled the vertices \(v_i^2\) with \(\{i,0)+(0,1)\}\) and vertices \(v_i^3\) with \(\{i,0)+(0,2)\}\). We can check that this construction produces a \(\Gamma\)-harmonious labeling of \(D_5^3\).
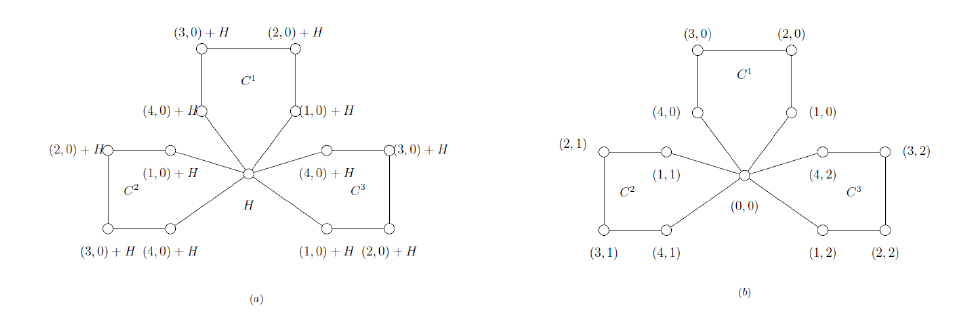
Theorem 21. When \(n\) and \(m\) are odd, then \(D_n^m\) is \(\Gamma\)-harmonious for any Abelian group \(\Gamma\) of order \(mn\).
Proof. We will use Observation 20 to construct a vertex labeling \(f\) of \(D_n^m\) with \(\Gamma\) that will induce a \(\Gamma\)-harmonious labeling of \(D_n^m\). For every \(n\)-cycle \(C^j\), choose a distinct element \(h_j\) in \(H\). This is possible because \(|H|=m\).
We start by labeling the central vertex \(u\) with \(\mathbf{0}\), the identity element of \(\Gamma\). If a vertex \(v_{i}^j\) in some \(C^j\) is labeled with \(g(v^j_i)=\gamma_i+H\) in the \(K\)-harmonious labeling of \(C^j\) constructed in Observation 20, then we label it with \(f(v^j_i)=\gamma_i+h_j\), where \(h_j\) is the chosen element of \(H\) for \(C^j\).
First we want to show that this construction produces a well-defined vertex labeling. Suppose that for some \(v^{j_1}_{i_1}\neq v^{j_2}_{i_2}\) we have \(f(v^{j_1}_{i_1})=f(v^{j_2}_{i_2})\).
\(f(v^{j_1}_{i_1})=\gamma_{i_1}+h_{j_1}= \gamma_{i_2}+h_{j_2}=f(v^{j_2}_{i_2})\) and
\[\label{eq:1} (\gamma_{i_1}+h_{j_1})+H=(\gamma_{i_2}+h_{j_2})+H.\tag{1}\] Because \(h_{j_1},h_{j_2}\in H\), we know that \[\label{eq:2} (\gamma_{i_1}+h_{j_1})+H= \gamma_{i_1}+H\tag{2}\]
and \[\label{eq:3} (\gamma_{i_2}+h_{j_2})+H= \gamma_{i_2}+H.\tag{3}\] Combining equations 1, 2 and 3, we obtain that \[\gamma_{i_1}+H=\gamma_{i_2}+H.\] But then \[g(v^{j_1}_{i_1})=\gamma_{i_1}+H=\gamma_{i_2}+H=g(v^{j_2}_{i_2})\]
and we have a contradiction, because in Observation 20 we have shown that \(g\) is injective. Moreover, if for some \(v^{j_0}_{i_0}\) we have \(f(v^{j_0}_{i_0})=\gamma_{i_0}+h_{j_0}= \mathbf{0},\) then \(\gamma_{i_0}\in H\), which again contradicts Observation 20. Therefore, this construction induces an injective vertex labeling.
Second, we must check if this construction induces a \(\Gamma\)-harmonious labeling of \(D_n^m\). We have to check whether there are any repetitions in the edge labels \(w_f(e)\) within a blade and across any two blades.
In \(C^j\) when \(w_g(e^j_i)=\tilde {\gamma}_i+H\), then \(w_f(e^j_i)=\tilde {\gamma}_i+kh_j\),where \(k\in \{1,2\}\). In particular, for edges \(uv^j_0\) and \(v^j_{n-1}\) we have \(k=1\), otherwise, \(k=2\).
For a fixed \(j\) and \(0\leq i\leq n-1\), we claim that each \(w_f(e^j_i)=\tilde {\gamma}_i+kh_j\) is distinct. For \(1\leq i\leq n-2\), each \(\tilde {\gamma}_i+2h_j\) is distinct because each label \(\tilde {\gamma}_i+H\) in \(C^j\) was distinct. Moreover, \(\tilde {\gamma}_0+h_j\neq \tilde {\gamma}_{n-1}+h_j\) for the same reason.
Now suppose that for a fixed \(j\) and some \(i\), \(1\leq i\leq n-2\), we have \(\tilde {\gamma}_0+h_j=\tilde {\gamma}_{i}+2h_j\). Then \(\tilde {\gamma}_{0}=\tilde {\gamma}_{i}+h_j\) and \[w_g(e_0)=\tilde {\gamma}_{0}+H=(\tilde {\gamma}_{i}+h_j)+H =\tilde {\gamma}_{i}+H =w_g(e_i),\] which is a contradiction by Observation 20. Similarly for \(2\leq i\leq n-2, w_f(e^j_{n-1})=\tilde {\gamma}_{n-1}+h_j\neq \tilde {\gamma}_{i}+2h_j=w_f(e^j_i)\).
Finally suppose for \(0\leq j_1<j_2\leq m\), and \(0\leq i_1\leq i_2\leq n-1\) two edge labels \(w_f(e^{j_1}_{i_1})\) and \(w_f(e^{j_2}_{i_2})\) across cycles \(C^{j_1}\) and \(C^{j_2}\) are the same.
Then \(\tilde {\gamma}_{i_1}+k_1 h_{j_1}= \tilde {\gamma}_{i_2}+k_2 h_{j_2}\), where \(k_1,k_2\in \{1,2\}\). Then similarly as above we have \[\tilde {\gamma}_{i_1}=\tilde {\gamma}_{i_2}+k_2h_{j_2}-k_1 h_{j_1} =\tilde {\gamma}_{i_2}+h^*\]
for some \(h^*\in H\). It follows that \[w_g(e_{i_1})=\tilde {\gamma}_{i_1}+H=(\tilde {\gamma}_{i_2}+h^*)+H =\tilde {\gamma}_{i^2}+H =w_g(e_{i_2}),\] a contradiction again. Thus, each edge label is distinct and the proof is complete. ◻
When \(n\) is even, we have a weaker theorem.
Theorem 22. For \(n\) even and \(m\) odd, \(D_n^m\) is \(\Gamma\)-harmonious when \(|\Gamma|=mn\), and \(\Gamma\) has a subgroup \(H\) or order \(m\) such that \(K=\Gamma/H\) satisfies the conditions in Theorem 8.
Proof. Let \(m\) be odd and \(n\) be even. If \(\Gamma\) has a subgroup of order \(m\) such that \(K=\Gamma/H\) satisfies the conditions in Theorem 8. Then, each \(C^j\) is \(K\)-harmonious labeling where \(u\) is labeled with \(H\). The construction then is same as in Theorem 21. ◻
When \(m\) is even, this construction does not work. As discussed in Theorem 21, the label of edge \(e_i^j\) is \(\tilde {\gamma}_i+kh_j\) for \(k=\{1,2\}\) and \(h_j\in H\). We know \(|H|=m\). Thus in \(H\), we can have two distinct elements \(h_j\) and \(h_{j'}\) such that \(2h_j=2h_{j'}\).
For generalized prisms, our result is again more general for \(n\) odd. This is because even cycles are not \(\Gamma\)-harmonious for all \(\Gamma\) of the proper order, while odd cycles are \(\Gamma\)-harmonious for all Abelian groups \(\Gamma\) of order \(n\) (see Theorem 6 or 8).
Recall that the number of edges of the generalized prism \(Y_{m,n}\) is \((2m-1)n\). The main idea of our construction is the following. Given a group \(\Gamma\) of order \((2m-1)n\) and a subgroup \(H\) of \(\Gamma\) of order \(n\) satisfying assumptions of Theorem 8 and assume that there is an \(H\)-harmonious labeling of \(C_n\). Then we label the vertices of each \(C_n\) by elements of a coset \(\beta+H\) where \(\beta\) is a generator of the cyclic quotient group \(\Gamma/H\) in a way corresponding to the original \(H\)-harmonious labeling. This way the edge labels of every “layer”, that is, either edges of a particular cycle or all edges between two consecutive cycles form a coset of \(\Gamma\).
We illustrate the method in two examples.
Example 4. We present a labeling of \(Y_{3,5}\) with \(Z_5\oplus Z_5\), starting with a labeling of \(C_5\) with \(Z_5\).
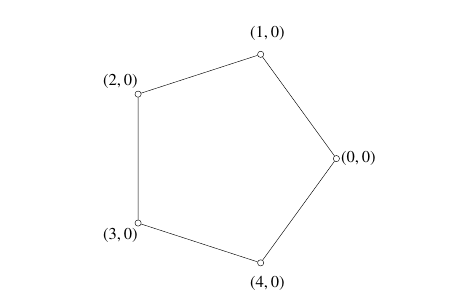
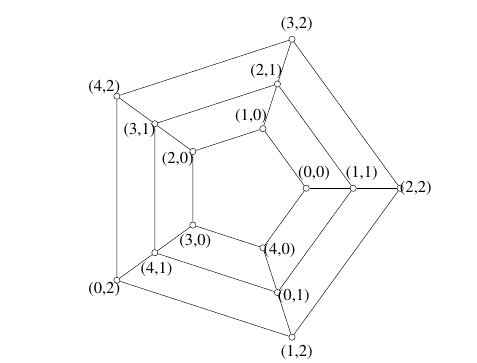
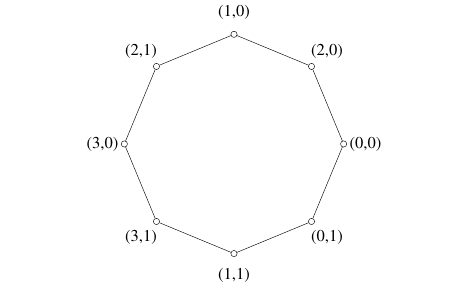
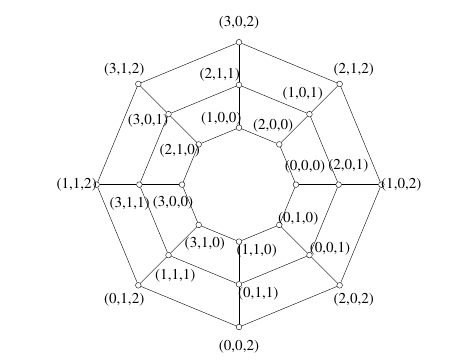
Example 5. We present a labeling of \(Y_{3,8}\) with \(Z_4\oplus Z_2\oplus Z_5\), starting with a labeling of \(C_8\) with \(Z_4\oplus Z_2\).
Theorem 23. Let \(n\geq3,m\geq2\) and \(\Gamma\) be an Abelian group of order \(n(2m-1)\). If \(\Gamma\) has a subgroup \(H\) of order \(n\) that satisfies the assumptions of Theorem 8, and the quotient group \(\Gamma/H\) is cyclic, then prism \(Y_{m,n}\cong P_m\Box C_n\) admits a \(\Gamma\)-harmonious labeling.
Proof. We will use the following notation. Each \(n\)-cycle \(C^j\) for \(j=0,1,\dots,m-1\) will consist of vertices \(x^j_i\) with \(i=1,2,\dots,n\) and edges \(x^j_ix^j_{i+1}\), where \(i=1,2,\dots, n\) and addition in the subscript is performed modulo \(n\). The paths \(P^i\) will consist of vertices \(x^0_i, x^1_{i+1},\dots,x^{m-1}_{i+m-1}\) and edges \(x^j_i x^{j+1}_{i+1}\) where \(i=1,2,\dots, n, j=0,1,\dots,m-2\) and addition in the subscript is again performed modulo \(n\). Thus, the path edges can be seen as “diagonal”, which is done for computational convenience.
Let \({H}\) be a subgroup \(\Gamma\) of order \(n\) that satisfies the assumptions of Theorem 8 and \(K=\Gamma/{H}\) be cyclic of order \(2m-1\) generated by a coset \(\beta+H\).
Hence there exists an \(H\)-harmonious labeling \(g\) of \(C_n=x_1,x_2,\dots,x_n\). For each \(x^j_i\) we now define \[f(x^j_i)=g(x_i) +j\beta.\] Then the label \(w(x^j_i x^j_{i+1})\) of an edge \(x^j_i x^j_{i+1}\) in cycle \(C^j\) is defined as \[\begin{aligned} w(x^j_i x^j_{i+1}) &= f(x^j_i) +f(x^j_{i+1})\\ &= (g(x_i) +j\beta) +(g(x_{i+1}) +j\beta)\\ &= g(x_i) +g(x_{i+1}) +2j\beta \\ &= w(x_i x_{i+1}) +2j\beta. \end{aligned}\] Now the set of all edge labels in \(C^j\) is \[\begin{aligned} W^j &=\{w(x^j_i x^j_{i+1})\mid i=1,2,\dots,n \} \\ &=\{w(x_i x_{i+1}) +2j\beta \mid i=1,2,\dots,n \}. \end{aligned}\]
Because \(g\) is an \(H\)-harmonious labeling, the set of all weights \(w(x_i x_{i+1})\) forms the subgroup \(H\) itself and \[\begin{aligned} W^j &=\{w(x_i x_{i+1}) +2j\beta \mid i=1,2,\dots,n \} =2j\beta+H, \end{aligned}\] an even coset in \(\Gamma/H\). Consequently, the labels of all edges in cycles \(C^0,C^1,\dots, C^m\) form all \(m\) even cosets \(H, 2\beta +H,\dots, 2(m-1)\beta +H\) of the cyclic group \(\Gamma/H\).
For paths, the label of \(x^j_i x^{j+1}_{i+1}\) is defined as \[\begin{aligned} w(x^j_i x^{j+1}_{i+1}) &= f(x^j_i) +f(x^{j+1}_{i+1})\\ &= (g(x_i) +j\beta) +(g(x_{i+1}) +(j+1)\beta) \\ &= g(x_i) +g(x_{i+1}) +(2j+1)\beta \\ &= w(x_i x_{i+1}) +(2j+1)\beta. \end{aligned}\] The set of labels of the path edges between cycles \(C^j\) and \(C^{j+1}\) for \(j=0,1,\dots,m-2\) is then \[\begin{aligned} U^j &=\{w(x^j_i x^{j+1}_{i+1})\mid i=1,2,\dots,n \} \\ &=\{w(x_i x_{i+1}) +(2j+1)\beta \mid i=1,2,\dots,n \} \end{aligned}\] the coset \((2j+1)\beta+H\). Therefore, the weights of all path edges form all \(m-1\) odd cosets \(\beta+H, 3\beta +H,\dots, (2m-3)\beta +H\) of \(\Gamma/H\).
Because we have \(j=0,1,\dots,m-1\), we obtained \(2m-1\) distinct cosets and their union forms the group \(\Gamma\). This completes the proof. ◻
For convenience, we express the above result in more explicit form, describing the group \(\Gamma\) in the nested form.
Corollary 1. Let \(n\geq3\) be odd, \(m\geq2\) and \(\Gamma\) an Abelian group of order \((2m-1)n\) with a cyclic subgroup \(K\) of order \(2m-1\). Then the prism \(Y_{m,n}\cong C_n\Box P_m\) admits a \(\Gamma\)-harmonious labeling.
Proof. By Theorem 5 part 2, there exists a subgroup \(H\) such that \(K\approx \Gamma/H\). Indeed, \(H\) is of order \(n\) and \(n\) is odd. Thus, by Theorem 8 there exists a \(H\)-harmonious labeling of \(C_n\). The result now follows from Theorem 23. ◻
Corollary 2. Let \(n\geq4\) be even, \(m\geq2\) and \(\Gamma\) an Abelian group of order \((2m-1)n\) written in the nested form as \(\Gamma=Z_{n_1}\oplus Z_{n_2}\oplus\dots\oplus Z_{n_t}\) where \(t\geq2\), with a cyclic subgroup \(K\) of order \(2m-1\). If
\(n_1\equiv0\pmod4\) and \(n_2\) is even, or
\(n_2\geq4\) is even,
then the prism \(Y_{m,n}\cong C_n\Box P_m\) admits a \(\Gamma\)-harmonious labeling.
Proof. By Observation 4, \(2m-1\) divides \(n_1\). By Theorem 5 part 2, there is a subgroup \(H\) such that \(K\approx \Gamma/H\). Moreover, \(H\) can be written as \(H=Z_{n'_1}\oplus Z_{n_2}\oplus\dots\oplus Z_{n_t}\), where \(n'_1=n_1/(2m-1)\).
When \(n_1\equiv0\pmod4\) and \(n_2\) is even, then also \(n'_1\equiv0\pmod4\) and \(H\) contains a subgroup isomorphic to \(Z_4\oplus Z_2\) and satisfies assumptions of Theorem 6. The result then follows from Theorems 8 and 23.
When \(n_2\geq4\) is even, then \(n_1\) is even as well. And because \(n_2\geq4\), \(H\) contains a subgroup isomorphic to \(Z_2\oplus Z_{2s}\) for \(s\geq2\). Therefore, the result follows again from Theorems 6, 8 and 23. ◻
For computation convenience, we slightly change the notation here and number the cycles of the generalized prism \(Y_{m,n}\) as \(C^1,C^2,\dots, C^m\).
A generalized closed web is then a graph arising from \(Y_{m,n}\) by adding a vertex \(x^0_{0}\) and joining it by an edge to every vertex of the top cycle \(C^1\) of \(Y_{m,n}\). The remaining vertices will follow the notation from Section 7.
The number of edges and order of \(\Gamma\) is now \(2mn\).
Theorem 24. Let \(n\geq3,m\geq2\) and \(\Gamma\) be an Abelian group of order \(2mn\). If \(\Gamma\) has a subgroup \(H\) of order \(n\) that satisfies assumptions of Theorem 8 and the quotient group \(\Gamma/H\) is cyclic, then the generalized closed web \(CW_{m,n}\) admits a \(\Gamma\)-harmonious labeling.
Proof. We will use the following notation. The central vertex of degree \(n\) will be denoted by \(x^0_{0}\). Each \(n\)-cycle \(C^j\) for \(j=1,2,\dots,m\) will consist of vertices \(x^j_i\) with \(i=1,2,\dots,n\) and edges \(x^j_ix^j_{i+1}\), where \(i=1,2,\dots, n\) and addition in the subscript is performed modulo \(n\). The paths \(P^i\) will consist of vertices \(x^0_0, x^1_{i},x^2_{i+1}\dots,x^{m-1}_{i+m-2}\) and edges \(x^0_0x^1_{i}\) and \(x^j_{i+j-1} x^{j+1}_{i+j}\) where \(i=1,2,\dots, n, \ j=1,2,\dots,m-1\) and addition in the subscript is again performed modulo \(n\).
The number of edges in \(CW_{m,n}\) is \(2mn\), which implies \(|\Gamma|=2mn\).
By our assumption, \(H\) satisfies conditions of Theorem 8 and therefore there exists an \(H\)-harmonious labeling \(g\) of \(C_n=x_1,x_2,\dots,x_n\). We first label the central vertex by the identity element of \(\Gamma\), that is, \[f(x^0_0) = e.\] The remaining vertices will be labeled as \[f(x^j_i)=g(x_i) +j\beta.\] Then the label \(w(x^j_i x^j_{i+1})\) of an edge \(x^j_i x^j_{i+1}\) in cycle \(C^j\) is defined as \[\begin{aligned} w(x^j_i x^j_{i+1}) &= f(x^j_i) +f(x^j_{i+1})\\ &= g(x_i) +g(x_{i+1}) +2j\beta \\ &= w(x_i x_{i+1}) +2j\beta \end{aligned}\] and the set of all edge labels in \(C^j\) is \[\begin{aligned} W^j &=\{w(x^j_i x^j_{i+1})\mid i=1,2,\dots,n \} \\ &=\{w(x_i x_{i+1}) +2j\beta \mid i=1,2,\dots,n \} \\ &= 2j\beta +H, \end{aligned}\] an even coset in the quotient group \(\Gamma/H\), because the set of weights of the edges in the cycle \(C_n\) forms the subgroup \(H\). This follows from our assumption that \(H\) allows an \(H\)-harmonious labeling \(g\).
Notice that in the cycle \(C^m\) we have \[\begin{aligned} W^m &= 2m\beta +H = H, \end{aligned}\] because \(\Gamma/H\) is cyclic of order \(2m\). Therefore, the labels of all edges in cycles \(C^1,C^2,\dots, C^m\) form all \(m\) even cosets \(H, 2\beta +H,\dots, (2m-2)\beta +H\) of the cyclic group \(\Gamma/H\).
For paths, the label of \(x^j_i x^{j+1}_{i+1}\) is defined as \[\begin{aligned} w(x^j_i x^{j+1}_{i+1}) &= f(x^j_i) +f(x^{j+1}_{i+1})\\ &= g(x_i) +g(x_{i+1}) +(2j+1)\beta \\ &= w(x_i x_{i+1}) +(2j+1)\beta. \end{aligned}\] The set of labels of the edges incident with the central vertex is \[\begin{aligned} U^0 &=\{w(x^0_0 x^{1}_{i})\mid i=1,2,\dots,n \} \\ &=\{f(x^0_0) + f(x^1_i) \mid i=1,2,\dots,n \} \\ &=\{e + g(x_i) +\beta \mid i=1,2,\dots,n \} \\ &= \beta +H, \end{aligned}\] because \(g\) is the \(H\)-harmonious labeling of the cycle \(C_n\) and therefore a bijection from the vertex set of \(C_n\) to \(H\).
For the remaining path edges, the set of labels between cycles \(C^j\) and \(C^{j+1}\) for \(j=1,2,\dots,m-1\) is \[\begin{aligned} U^j &=\{w(x^j_i x^{j+1}_{i+1})\mid i=1,2,\dots,n \} \\ &=\{w(x_i x_{i+1}) +(2j+1)\beta \mid i=1,2,\dots,n \} \\ &= (2j+1) +H. \end{aligned}\] Hence, the weights of all path edges form all \(m\) odd cosets \(\beta+H, 3\beta +H,\dots, (2m-1)\beta +H\) of \(\Gamma/H\).
We obtained \(2m\) distinct cosets and their union forms the group \(\Gamma\). This completes the proof. ◻
Example 6. A \(Z_5\oplus Z_6\)-harmonious labeling of the closed web \(CW_{3,5}\).
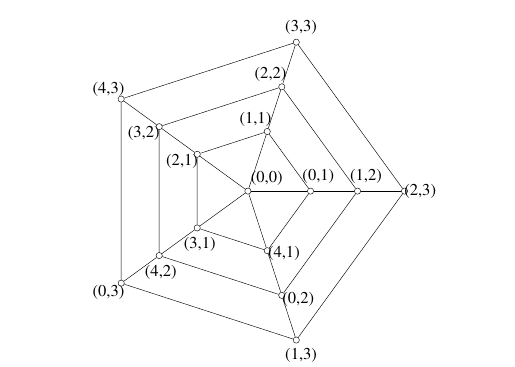
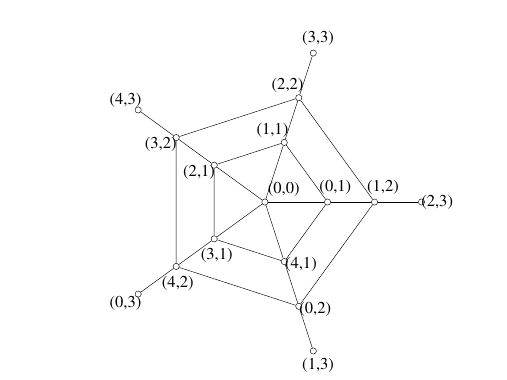
Example 7. A \(Z_4\oplus Z_2\oplus Z_6\)-harmonious labeling of the closed web \(CW_{3,8}\).
Recall that Seoud and Youssef [9]proved that closed webs \(CW_{2,n}\) are harmonious for all odd \(n\). A special case of the previous theorem generalizes their result as follows.
Corollary 3. The closed web \(CW_{m,n}\) is harmonious for all odd \(n\geq3\) and any \(m\geq2\).
We again express the previous result of Theorem 24 in terms of the nested form of \(\Gamma\).
Corollary 4. Let \(n\geq3\) be odd, \(m\geq2\) and \(\Gamma\) an Abelian group of order \(2mn\) with a cyclic subgroup of order \(2m\). Then the closed web \(CW_{m,n}\) is \(\Gamma\)-harmonious.
Proof. Similarly as in the proof of Corollary 1, this follows from Theorems 6, 8, and 24. ◻
For even \(n\), the explicit expression is broken into several cases.
Corollary 5. Let \(n\geq4\) be even, \(m\geq2\) and \(\Gamma\) an Abelian group of order \(2mn\) written in the nested form as \(\Gamma=Z_{n_1}\oplus Z_{n_2}\oplus\dots\oplus Z_{n_t}\) where \(t\geq2\), with a cyclic subgroup of order \(2m\). If
\(n_1\equiv0\pmod{8m}\) and \(n_2\equiv0\pmod{2}\), or
\(n_1\equiv0\pmod{4m}\), \(n_2\equiv0\pmod{2}\), \(n_2\geq4\), or
\(n_1\equiv0\pmod{2m}\), \(n_2\equiv0\pmod{4}\) and \(n_3\equiv0\pmod{2}\), or
\(n_1\equiv0\pmod{2m}\), \(n_3\equiv0\pmod{2}\) and \(n_t>1\) is odd,
then the closed web \(CW_{m,n}\) is \(\Gamma\)-harmonious.
Proof. We again denote \(n'_1=n_1/(2m)\). By similar reasoning as in the proof of Corollary 2, \(\Gamma\) has a subgroup \(H\approx Z_{n'_1}\oplus Z_{n_2}\oplus\dots\oplus Z_{n_t}\).
In Case (1), because \(n_1\equiv0\pmod{8m}\), \(n'_1\equiv0\pmod{4}\) and \(H\) has a subgroup isomorphic to \(Z_4\oplus Z_2\). Indeed, \(\Gamma/H\) is cyclic of order \(2m\).
In Case (2), because \(n_1\equiv0\pmod{4m}\), \(n'_1\equiv0\pmod{2}\) and \(H\) has a subgroup isomorphic to \(Z_2\oplus Z_{2s}\) with \(s\geq 2\) because \(n_2\geq4\).
In Case (3), because \(n_2\equiv0\pmod{4}\) and \(n_3\equiv0\pmod{2}\), \(H\) has a subgroup isomorphic to \(Z_4\oplus Z_2\).
Finally, in Case (4), \(n_2\) is even because \(n_3\) is even. Because \(n_t>1\) is odd, we must have \(n_3=2s\) where \(s\geq n_t\geq3\), because \(n_t\) divides \(n_3\).
Therefore, the proof again follows from Theorems 6, 8 and 24. ◻
A generalized open web \(OW_{m,n}\) is the graph arising from the generalized closed web \(CW_{m,n}\) by removing the edges of the bottom \(n\)-cycle \(C^m\). The number of edges and order of \(\Gamma\) is then \((2m-1)n\).
The proof of the following theorem is just a slight modification of the proof of Theorem 24 and is left to the reader.
Theorem 25. Let \(n\geq3,m\geq2\) and \(\Gamma\) be an Abelian group of order \((2m-1)n\). If \(\Gamma\) has a subgroup \(H\) of order \(n\) that satisfies the assumptions of Theorem 8 and the quotient group \(\Gamma/H\) is cyclic, then the generalized open web \(OW_{m,n}\) admits a \(\Gamma\)-harmonious labeling.
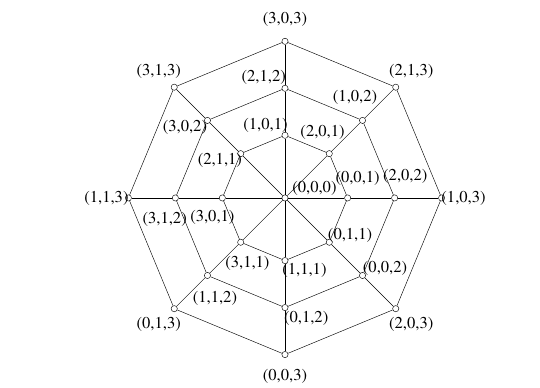
Example 8. A \(Z_5\oplus Z_5\)-harmonious labeling of the open web \(OW_{3,5}\).
Example 9. A \(Z_4\oplus Z_2\oplus Z_5\)-harmonious labeling of the open web \(OW_{3,5}\).
Seoud and Youssef [9]and Gnanajothi [6]proved that open webs \(OW_{m,n}\) are harmonious for all odd \(n\) and \(m=2\) and 3, respectively. We state a generalization following directly from the previous theorem as a corollary.
Corollary 6. The open web \(OW_{m,n}\) is harmonious for all odd \(n\) and any \(m\geq2\).
For convenience, we again express the result of Theorem 25 in a more explicit form, describing the group \(\Gamma\) in the nested form.
Corollary 7. Let \(n\geq3\) be odd, \(m\geq2\) and \(\Gamma\) an Abelian group of order \((2m-1)n\) with a cyclic subgroup of order \(2m-1\). Then the open web \(OW_{m,n}\) admits a \(\Gamma\)-harmonious labeling.
Proof. This follows directly from Theorems 6, 8 and 25. ◻
Corollary 8. Let \(n\geq4\) be even, \(m\geq2\) and \(\Gamma\) an Abelian group of order \((2m-1)n\) with a cyclic subgroup of order \(2m-1\) written in the nested form as \(\Gamma=Z_{n_1}\oplus Z_{n_2}\oplus\dots\oplus Z_{n_t}\), where \(t\geq2\). If
\(n_1\equiv0\pmod4\) and \(n_2\) is even, or
\(n_2\geq4\) is even,
then the web \(OW_{m,n}\) admits a \(\Gamma\)-harmonious labeling.
The proofs are identical to the proofs of Corollaries 1 and 2, respectively.
We explored \(\Gamma\)-harmonious labeling, a generalization of a well-known notion of harmonious labeling, for several families of cycles-related graphs. In most cases, our results are only partial. Therefore, we state some open problems here.
There are two main directions for further research. One is dealing with graphs based on even cycles where the group \(\Gamma\) does not contain a subgroup isomorphic to \(Z_4\oplus Z_2\).
Problem 1. Determine for what Abelian groups \(\Gamma\) not containing a subgroup of order \(n\) isomorphic to \(Z_2\oplus Z_{2s}, s\geq2\) there exists a \(\Gamma\)-harmonious labeling of generalized prisms \(Y_{m,n}\), open and closed webs \(OW_{m,n}\), \(CW_{m,n}\) and superwheels \(SW_{k,n}\) for even \(n\).
For Dutch windmill graphs, we only covered the cases when the number of cycles is odd. When the cycle length was even, we have an additional restriction on the quotient group. We propose the following two problems on Dutch windmill graphs.
Problem 2. Determine for what Abelian groups \(\Gamma\) there exists a \(\Gamma\)-harmonious labeling of Dutch windmill graphs \(D^m_{n}\) for even \(m\).
Problem 3. Determine for what Abelian groups \(\Gamma\) there exists a \(\Gamma\)-harmonious labeling of Dutch windmill graphs \(D^m_{n}\) for odd \(m\) and even \(n\) when there does not exist a subgroup \(H\) of order \(m\) such that \(K=\Gamma/H\) satisfies the conditions in Theorem 8.
The other direction concerns graphs \(Y_{m,n}\) and \(OW_{m,n}\) when \(\Gamma\) does not have a cyclic subgroup of order \(2m-1\) or \(CW_{m,n}\) when \(\Gamma\) does not have a cyclic subgroup of order \(2m\).
Problem 4. Determine for what Abelian groups \(\Gamma\) not containing a cyclic subgroup
of order \(2m-1\) there exists a \(\Gamma\)-harmonious labeling of generalized prisms \(Y_{m,n}\) and open webs \(OW_{m,n}\)
of order \(2m\) there exists a \(\Gamma\)-harmonious labeling of closed webs \(CW_{m,n}\).
We also want to express out thanks to Alexa Hedtke and Johnathan Koch for their contribution to our results in the early stages of this project. Johnathan Koch wrote a program in python which we used to check if a \(\Gamma\)-harmonious labeling existed for a given graph and if such labeling existed, it gave us the exact labeling. The program helped us to find counterexamples and investigate patterns. The program can be found here [10].