Radio number of cartesian products of complete bipartite graphs and odd cycles

1. Introduction

In the era of rapid development of Internet, wireless communication has become an indispensable part of communication network. However, with the increasing number of users, the scale of the network has also expanded, which makes the limitations of the network become more obvious. With the rapid development of wireless communication networks in recent years, it has changed the way people communicate. But wireless communication network still has many limitations, the limited channel resources influence the fairy tale quality of communication network. Although many scholars continue to optimize the channel assignment algorithm to solve the insufficient utilization of channel resources in wireless communication networks, as well as the influence of inter-channel interference on the quality of communication. In 2024, Shin and Lee et al. [17] proposed an approximate algorithm to improve the performance of multi-radio and multi-channel wireless mesh networks based on theoretical model drive. Skalli, Ghosh et al. [18] put forward the problem and solution of channel allocation strategy for multi-channel wireless networks.

The optimal channel assignment strategy for wireless communication networks has attracted the research interest of many scholars. Griggs [5] proposed in the 2-distance label that the geographical location between sites will affect the degree of interference, and strong interference will be generated when two sites are close to each other, so that the distance between two adjacent vertices is at least 2. In fact, in 2001, Chartrand and Erwin [3] proposed the definition of radio label. Radio label is also known as multi-level distance label, which is a mapping function. In order to assign each endpoint of the graph to different vertex labels, the edge between any two adjacent vertices has the minimum weight. Moreover, each vertex is assigned a unique label. The mapping function of the radio label is as follows:

$$\theta :V(G)\to Z^{+}\cup 0,$$ such that $$|\theta (x)-\theta (y)|\ge diam(G)+1-d(x,y),\mathrm{\forall }x,y\in V(G).$$

$|\theta (x)-\theta (y)|$ is the span of the radio label of vertex $x$ and $y$ in $G$, then the span of the radio label of graph $G$ is $span(\theta )=max|\theta (x)-\theta (y)|$, and the number of radios in $G$ is represented by $rn(G)$. The radio number of graph $G$ is obtained from the span of the radio label, denoted by $rn(G)=min\{span(\theta )\}$, which is the minimum span of the radio label. Hale first proposed the channel assignment problem in 1980 [6], and then Roberts proposed to transform the channel assignment problem into the graph vertex labeling problem [15]. According to the nature of the interconnection network, the graph was used to simulate the network structure of wireless communication. The binary set $(V,E)$ of the graph represents the stations of the wireless communication network and the relationships between the stations respectively, that is, the physical lines in the network.

The construction of large-scale network in wireless communication network is a complicated and tedious work. When using graph to simulate the topology structure of large-scale network, according to the knowledge of graph theory, product graph can be used to simulate the topology structure of large-scale network. Let graph $G$ be a binary $(V,E)$, where $V$ is the vertex set of $G$ and $E$ is the edge set of $G$. If we take any two vertices $x,y\in V(G)$, then in the definition of radio label $\theta (x)$ is the multi-level distance of vertex $x$, that is, the radio label, and $d(x,y)$ is the shortest distance between vertex $x$ and vertex $y$ in $G$, and $diam(G)$ represents the diameter of $G$, which is the maximum of the shortest distance between any two vertices in the graph.

Sabidussi [16] proposed the concept of Cartesian product and several other products for the first time. Let $Q=\{V_1,E_1\}$ and $H=\{V_2,E_2\}$ be two undirected graphs, then graph $G$ is the Cartesian product graph of $Q$ and $H$, denoted as $G=Q\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}H$. The set of vertices $V(G)=V(Q)\times V(H)$, take any two vertices $xy\in V(Q)$ and $ab\in V(H)$ in $G$, such that the two vertices are adjacent if and only if $x=a,yb\in E(H)$ or $y=b,xa\in E(Q)$, and graphs $Q$ and $H$ are called factor graphs of $G$.

When the properties of two graphs formed by a Cartesian product change, it becomes difficult to analyze the topology of the product graph, but its properties are relatively easy to analyze for special graphs, so the radio number of the product graph of some special graphs has been determined, such as Yenoke and Selvagopal et al. [22] have determined the boundary of the radio number of the enhanced mesh; Yenoke and Kaabar [21] studied the self-named nanostar tree dendrimers, and mainly obtained the distance 2 label and radio number of the nanostar tree dendrimers. Rajan and Yenoke [14] studied hexagonal mesh and obtained the span of its radio labels. Morris-Rivera and Tomova [12] studied the radio number of the cycle itself and its Cartesian product on the basis of the radio number of the cycle; ELrokh, Al-Shamiri [4] studied the radio numbers of graphs such as paths, cycles, stars and double stars, and obtained a novel radio label of graphs, and the upper limit of its radio geometric mean was obtained by a new algorithm. Arputha Jose and Daniel Raj [1] found the span of quadrilateral snake families through the vertex labeling problem of the graph; Khennoufa and Togni [9] determined the number of radios for the hypercube; Radio numbers for other graphs have also been derived, such as cactus graphs, splitting graphs, and certain sunflower extended graphs etc, see [8,2,7,10,11,23,19,13].

It is a challenging problem to find the optimal channel assignment strategy by simulating the wireless communication network by the graph and using the vertex labeling problem of the product and graph to assign channels to the large network. Therefore, the channel assignment problem of communication network is studied by using the Cartesian product. This paper focuses on the lower bound of the radio number of the Cartesian product of a complete bipartite graph $K_{a,b}$ and cycles of order $m$, where $m\ge 5$ is odd and $a+b=n$.

2. Main results

Definition 2.2. Let $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ be the Cartesian product of an $n$-vertex complete bipartite graph and an $m$-order cycle, where $a+b=n$, $1\le a,b\le n-1$, $m\ge 5$ and odd. Take any $i$ subgraph of $G$ and denote it as $t(i)$, $i\in [1,m]$. Its vertex set is $V\left(t\left(i\right)\right)=V_1\left(i\right),V_2\left(i\right),\dots ,V_m\left(i\right)$, which can be seen from the topology of $G$. The graph $G$ contains $m$ $t(i)$ subgraphs.

Lemma 2.3.[20] Let $G_j$ be a connected graph, when the graph $G$ obtained by the Cartesian product of $n$ connected graphs $G_j$, and the order of the product factor graph $G_j$ is $n_j$, $1\le j\le n$, then the diameter of the Cartesian product graph $G$ is: $$\begin{array}{}\text{(1)}& \begin{array}{rl}diam(G)& =diam(G_1\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{G}_2\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}\dots \mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{G}_m)\\ & =diam(G_1)+diam(G_2)+\dots +diam(G_m).\end{array}\end{array}$$

Corollary 2.4. Let $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ be the Cartesian product of an $n$-vertex complete bipartite graph and an odd cycle of order $m$, where $a+b=n$, $1\le a,b\le n-1$, $m\ge 5$ and is odd, then $diam(G)=\frac{m-1}{2}+2$.

Definition 2.5. Let $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ be the Cartesian product graph of a complete bipartite graph with $n$ vertices and an odd cycle of order $m$. Choose three subgraphs $t(1)$, $t(\frac{m+1}{2})$ and $t(m)$ in $G$ and denote them as $G(\ast )$, respectively. The vertices of these three subgraphs are $V(1)$, $V(\frac{m+1}{2})$, and $V(m)$. Let $P^{\prime }(h)$ be a class of paths in $G(\ast )$, and $\alpha$ and $\beta$ be the shortest distances between two vertices on that path. Assuming that $P^{\prime }(h)=V_j(1)\stackrel{\alpha }{⟶}$ $V_k(\frac{m+1}{2})\stackrel{\beta }{⟶}{V}_l(m)$, such that $j\ne k\ne l$, $V_j(1)\in V(1)$, $V_k(\frac{m+1}{2})\in V(\frac{m+1}{2}),V_l(m)\in V(m)$, and $1\le j,k,l\le n$. It can be verified that $P^{\prime }(h)$ contains three cases, defined as follows without loss of generality: $$\begin{array}{}\text{(2)}& \{\begin{array}{l}{P}_1^{\prime }(h)=\{v_1(1)\stackrel{\frac{m+3}{2}}{⟶}{v}_3\left(\frac{m+1}{2}\right)\stackrel{\frac{m+3}{2}}{⟶}{v}_2(m)\};\\ P_2^{\prime }(h)=\{v_3(1)\stackrel{\frac{m+3}{2}}{⟶}{v}_2\left(\frac{m+1}{2}\right)\stackrel{\frac{m+1}{2}}{⟶}{v}_1(m),v_2(1)\stackrel{\frac{m+1}{2}}{⟶}{v}_1\left(\frac{m+1}{2}\right)\stackrel{\frac{m+3}{2}}{⟶}{v}_3(m)\};\\ P_3^{\prime }(h)=\{v_a(1)\stackrel{\frac{m+1}{2}}{⟶}{v}_b\left(\frac{m+1}{2}\right)\stackrel{\frac{m+1}{2}}{⟶}{v}_c(m),a\ne b\ne c,4\le a,b,c\le n\}.\end{array}\end{array}$$

Theorem 2.6. Let $\theta$ be the radio label of $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$, where $a+b=n$, $1\le a,b\le n-1$, $m\ge 5$ and odd. Choosing any vertex $v\in V(\frac{m+1}{2})$, if $\theta$ is the maximum vertex label, then $$\begin{array}{}\text{(3)}& \theta (v)=\{\begin{array}{rl}\frac{m+3}{2},& ifv\in \{v_1\left(\frac{m+1}{2}\right),v_2\left(\frac{m+1}{2}\right)\},\\ \frac{m+1}{2},& ifv\in v_3\left(\frac{m+1}{2}\right),\\ \frac{m+5}{2},& otherwise.\end{array}\end{array}$$

Proof. Let $P^{\prime }(h)\subset K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$, that any vertex on $V(P^{\prime }\left(h\right)$ has a radio label based on $diam\left(K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m\right)$, and for $u,v\in V(P^{\prime }\left(h\right))$, the distance between the vertices $u$ and $v$ is denoted as $k$, that is, $d(u,v)=k$, then the three cases of $P^{\prime }(h)$ are discussed respectively.

Case 1: For $P_1^{\prime }(h)=v_1(1)\stackrel{\frac{m+3}{2}}{⟶}{v}_3(\frac{m+1}{2})\stackrel{\frac{m+3}{2}}{⟶}{v}_2(m)$, its path is shown in red in Figure 1. Let $V_1\left(1\right)$ be the central vertex of $t(1)$, and satisfy $\theta \left(V_1\left(1\right)\right)=0$. According to the topology of the Cartesian product graph, $V_1\left(1\right)$ and $V_2\left(m\right)$ are in the same part, and the path between them is: $V_1\left(1\right)\to V_2\left(1\right)\to V_2\left(i\right)\to V_2\left(m\right)$, from the definition of complete bipartite graph, If $V_2\left(i\right)$ and $V_2\left(m\right)$ are not in the same part, then $$\begin{array}{}\text{(4)}& d(V_1\left(1\right),V_2\left(m\right))=3.\end{array}$$

According to the definition of radio labeling and Eq. (5), we can get $$\begin{array}{}\text{(5)}& \theta \left(V_2\left(m\right)\right)\ge \theta \left(V_1\left(1\right)\right)+diam\left(G\right)+1-d(V_1\left(1\right),V_2\left(m\right))\ge \frac{m-1}{2}.\end{array}$$

Similarly, by the topology of the $G$ is $d(V_2(m),V_3(\frac{m+1}{2}))=\frac{m+3}{2}$, then

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\theta \left(V_3\left(\frac{m+1}{2}\right)\right)& \ge \theta \left(V_2\left(m\right)\right)+diam\left(G\right)+1-d(V_2\left(m\right),V_3\left(\frac{m+1}{2}\right))\\ & \ge \frac{m+1}{2}.\end{array}\end{array}$$

Case 2(a): For $P_2^{\prime }(h)=v_3(1)\stackrel{\frac{m+3}{2}}{⟶}{v}_2(\frac{m+1}{2})\stackrel{\frac{m+1}{2}}{⟶}{v}_1(m)$, let $V_3(1)$ be the center vertex of $t(1)$, and satisfy $\theta (V_3(1))=0$. According to the definition of a complete bipartite graph, $d(V_3(1),V_1(m))=3$. Its path is shown in red in Figure 2. Defined by radio labels: $$\begin{array}{}\text{(7)}& \begin{array}{r}\theta \left(V_1\left(m\right)\right)\ge \theta \left(V_3\left(1\right)\right)+diam\left(G\right)+1-d(V_3\left(1\right),V_1(m))\ge \frac{m-1}{2}.\end{array}\end{array}$$

Similarly, by the topological structure of $G$, $d(V_1(m),V_2(\frac{m+1}{2}))=\frac{m+1}{2}$, then

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\theta \left(V_2\left(\frac{m+1}{2}\right)\right)& \ge \theta \left(V_1\left(m\right)\right)+diam\left(G\right)+1-d(V_1\left(m\right),V_2\left(\frac{m+1}{2}\right))\\ & \ge \frac{m+3}{2}.\end{array}\end{array}$$

Case 2(b): For $P_2^{\prime }(h)=v_2(1)\stackrel{\frac{m+1}{2}}{⟶}{v}_1(\frac{m+1}{2})\stackrel{\frac{m+3}{2}}{⟶}{v}_3(m)$, let $V_2(1)$ be the center vertex of $t(1)$, and $\theta (V_2(1))=0$. According to the definition of a complete bipartite graph, $d(V_2(1),V_3(m))=2$. Its path is shown in blue in Figure 2. Defined by radio labels:

$$\begin{array}{}\text{(9)}& \theta \left(V_3\left(m\right)\right)\ge \theta \left(V_2\left(1\right)\right)+diam\left(G\right)+1-d(V_2\left(1\right),V_3\left(m\right))\ge \frac{m+1}{2}.\end{array}$$

Similarly, by the topological of $G$, $d(V_3(m),V_1(\frac{m+1}{2}))=\frac{m+3}{2}$, then $$\begin{array}{}\text{(10)}& \begin{array}{rl}\theta \left(V_1\left(\frac{m+1}{2}\right)\right)& \ge \theta \left(V_3\left(m\right)\right)+diam\left(G\right)+1-d(V_3\left(m\right),V_1\left(\frac{m+1}{2}\right))\\ & \ge \frac{m+3}{2}.\end{array}\end{array}$$

Case 3: For $P_3^{\prime }(h)=\{v_a(1)\stackrel{\frac{m+1}{2}}{⟶}{v}_b\frac{m+1}{2})\stackrel{\frac{m+1}{2}}{⟶}{v}_c(m),4\le a,b,c\le n\}$. Its path is shown in blue in Figure 1. Let $V_a(1)$ be the central vertex of $t(1)$ and satisfy $\theta (V_a(1))=0$. According to the definition of a complete bipartite graph, $V_a(1)$ and $V_c(m)$ are not in the same part, so $d(V_a(1),V_c(m))=2$. Defined by radio labels: $$\begin{array}{}\text{(11)}& \theta \left(V_c\left(m\right)\right)\ge \theta \left(V_a\left(1\right)\right)+diam\left(G\right)+1-d(V_a\left(1\right),V_b\left(m\right))\ge \frac{m+1}{2}.\end{array}$$

Also, according to the definition of a complete bipartite graph, $V_3(m)$ and $V_1(\frac{m+1}{2})$ are not in the same part, so, $d(V_c(m),V_b(\frac{m+1}{2}))=\frac{m+1}{2}$. According to radio labellings, then $$\begin{array}{}\text{(12)}& \begin{array}{rl}\theta \left(V_b\left(\frac{m+1}{2}\right)\right)& \ge \theta \left(V_c\left(m\right)\right)+diam\left(G\right)+1-d(V_c\left(m\right),V_b\left(\frac{m+1}{2}\right))\\ & \ge \frac{m+5}{2}.\end{array}\end{array}$$ 

Definition 2.8. Let $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ be the Cartesian product of a complete bipartite graph of $n$ vertices and an odd cycle of order $m$, where $a+b=n$, $1\le a,b\le n-1$, $m\ge 5$ is odd. Subgraph $t(i)$ and $t(i+\frac{m+1}{2})$ is made up of $V(i)$ and $V(i+\frac{m+1}{2})$ of the vertex set of induced subgraph, subgraph $t(i)$ and $t(i+\frac{m+1}{2})$ remember to $G^{″}(i)\subseteq G$, where $i\notin \{1,\frac{m+1}{2},m\}$. When $m$ is odd, the graph $G$ has $\frac{m-3}{2}$ $G^{″}(i)$ subgraphs and the diameter of $G^{″}\left(i\right)$ is $\frac{m+3}{2}$.

Theorem 2.9. Let $G(\ast )$ be a subgraph induced by all endpoints and central vertices in $P^{\prime }(h)$ and be a subgraph of $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$, that is, $t\left(1\right),t\left(\frac{m+1}{2}\right),t(m)$, then the radio number of $G(\ast )$ in $G$ is $rn(G(\ast ))\ge \frac{2mn+6n-a\times (m+1)-8}{2}$.

Definition 2.10. Let $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ be the Cartesian product of a complete bipartite graph of $n$ vertices and an odd cycle of order $m$, where $a+b=n$, $1\le a,b\le n-1$, $m\ge 5$ is odd, and likewise, we define $G(\ast \ast )$ as a subgraph induced by $t(i)$, where $i\in [2,m-1]$, $i\notin \frac{m+1}{2}$, and $G(\ast \ast )=G\mathrm{\setminus }G(\ast )$.

Definition 2.11. Let $G^{″}(i)\subseteq G(\ast \ast )$ be a subgraph of $K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$, where $a+b=n$, $1\le a,b\le n-1$, $m\ge 5$ and is odd. Such that $G^{″}(i)$ is a subgraph induced by $t(j)$ and $t(j+\frac{m+1}{2})$, and $G(\ast \ast )\subset K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ contains $\frac{m-3}{2}$ $G^{″}(i)$ subgraphs.

Definition 2.12. Let $G^{″}(i)\subset K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ be a subgraph of $G$, then $rn(G^{\mathrm{\prime }\mathrm{\prime }}(i))\ge 2n+m-1$.

An important result of this paper is given below, which is the lower bound of the radio number of the Cartesian product graph of a complete bipartite graph with $n$ vertices an odd cycle of order $m$.

Theorem 2.13 Let $G=K_{a,b}\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}{C}_m$ be the Cartesian product of an $n$-vertex complete bipartite graph and an odd cycle of order $m$, where $a+b=n$, $1\le a,b\le n-1$, $m\ge 5$ and is odd. Then $rn(G)\ge \frac{1}{2}(m^2+4mn-2m-a\times (m+1)-14)$.

3. Application and numerical simulation

In wireless communication networks, radio antennas use radio labels in different bands of the spectrum to switch signals so that each station is assigned a unique number. However, the problem of limited resources and insufficient utilization in network communication leads to signal transmission interference. Many scholars solve this problem by optimizing algorithms constantly to reduce the interference in the communication process as much as possible. There are also many people using machine learning methods, neural networks and other advanced technologies to achieve the optimization of channel assignment.

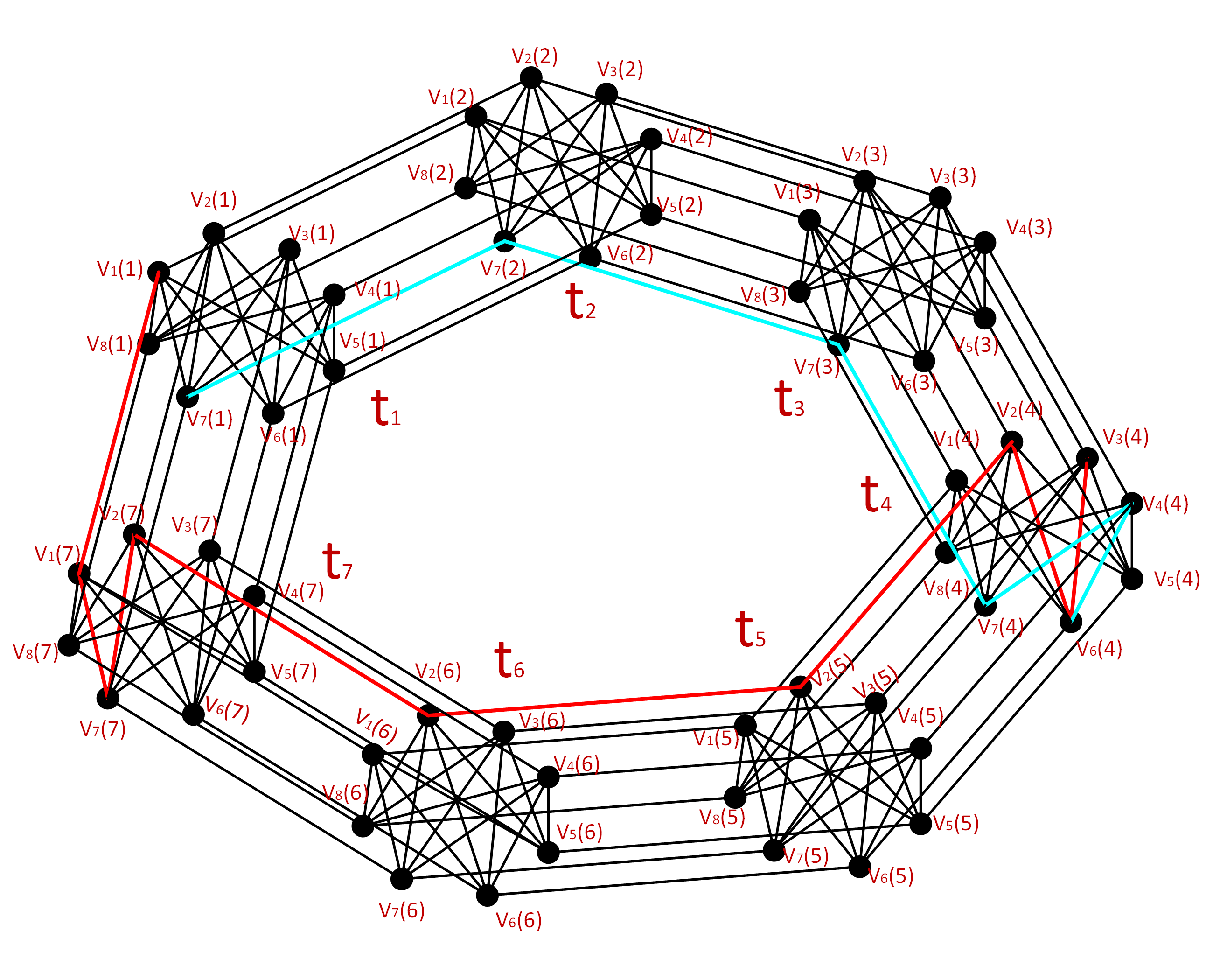
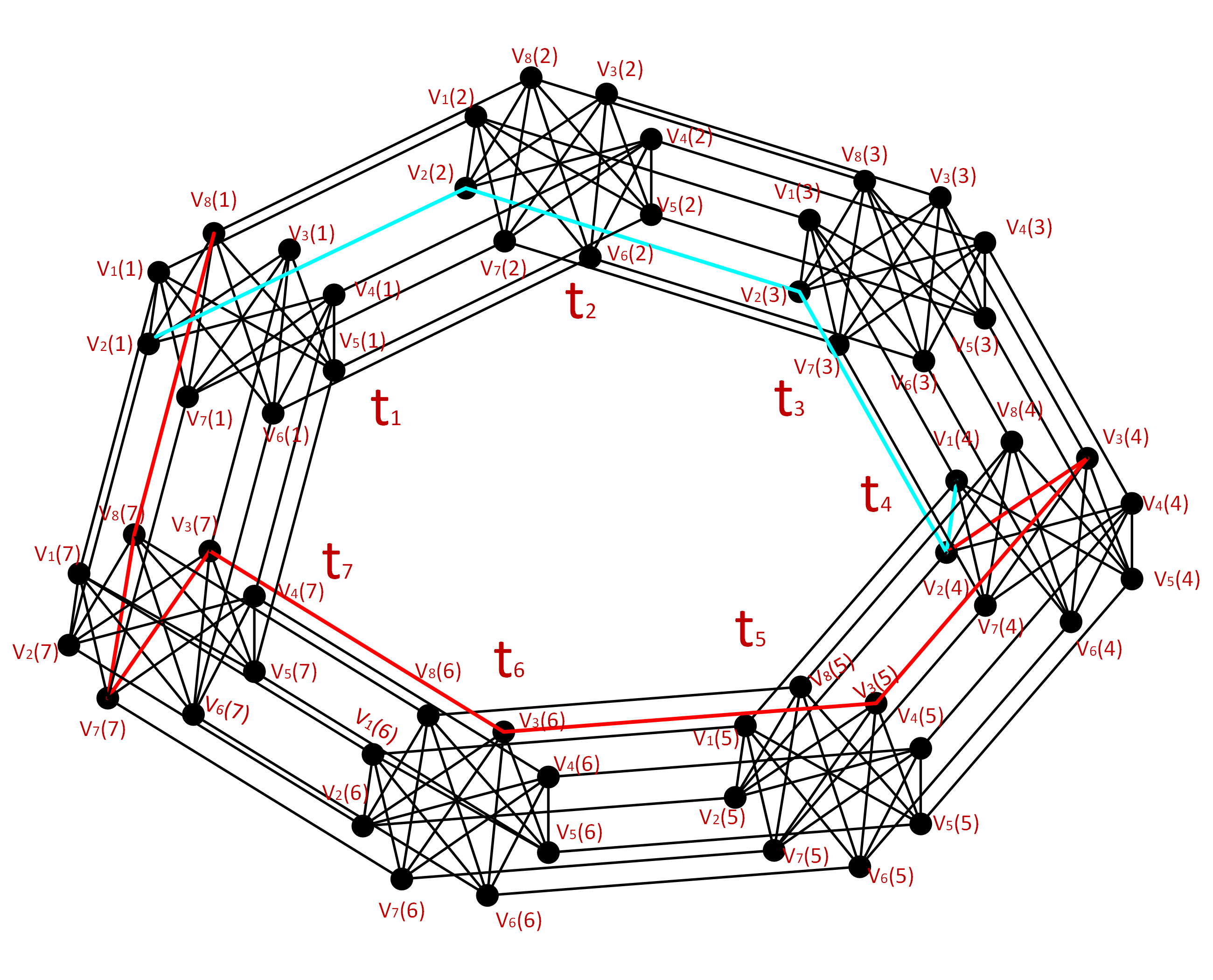
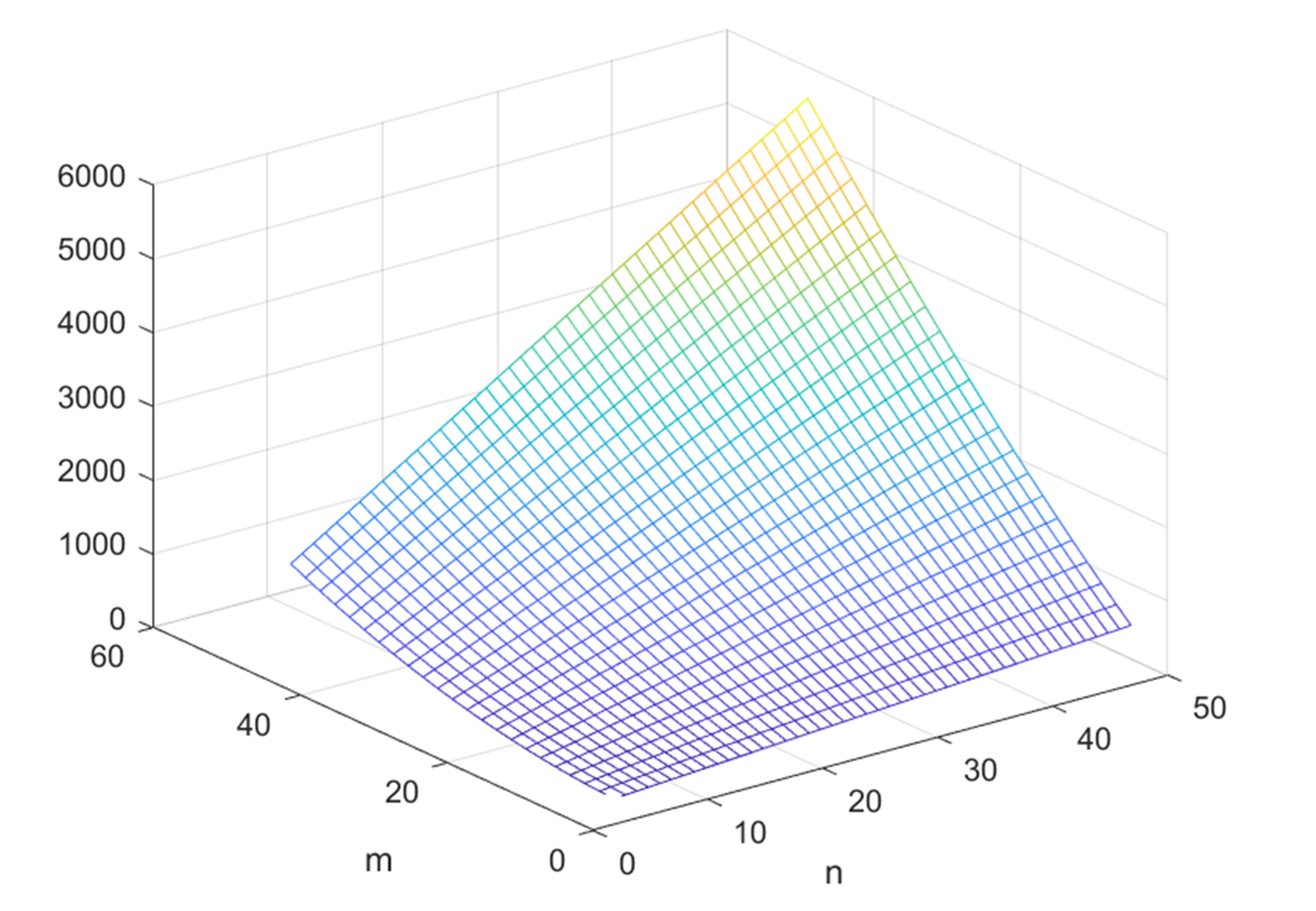
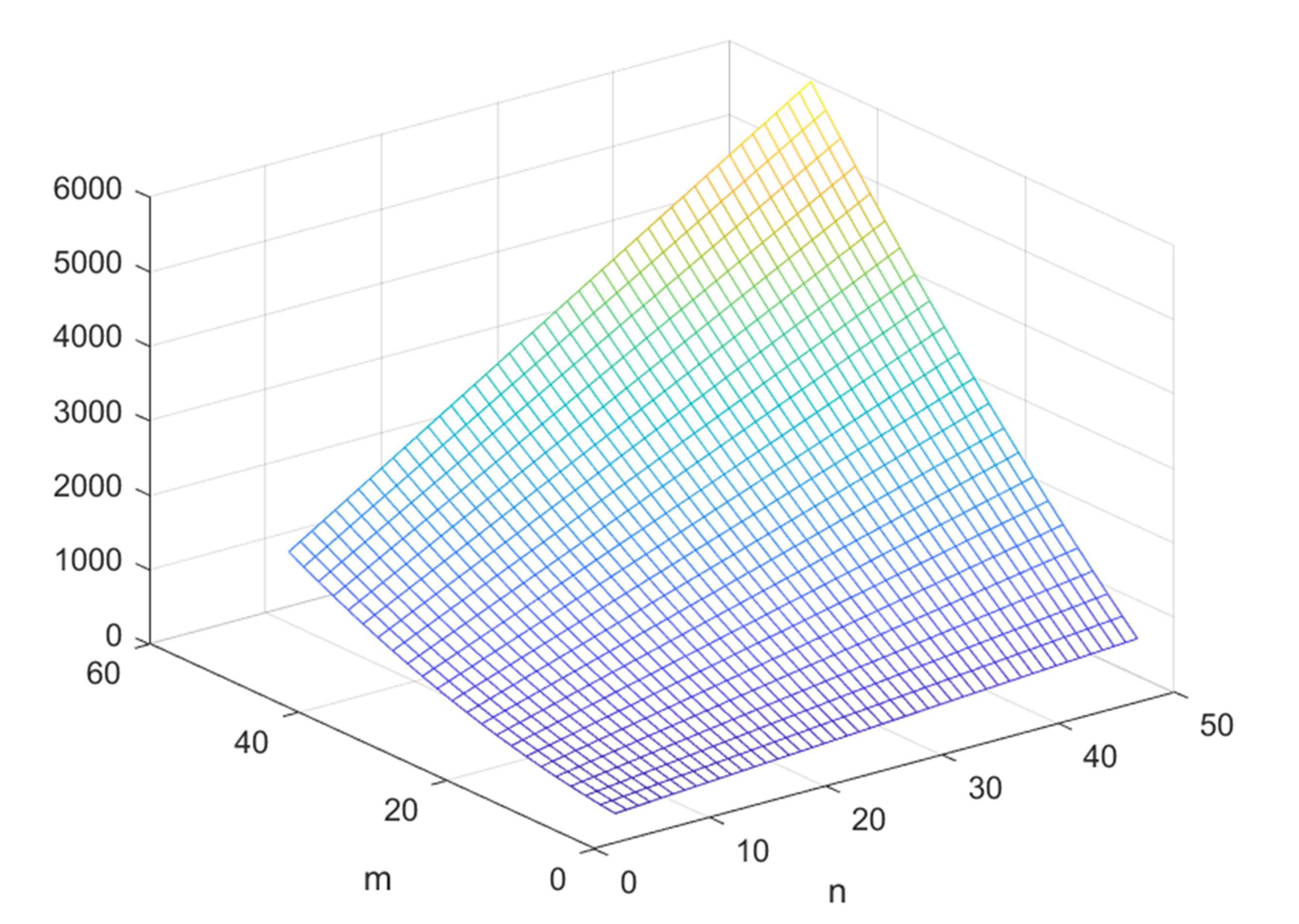
According to the above two examples, we can clearly see that when the city adopts the same topology structure for channel assignment, the channel assignment strategy is different when the number of stations in the two areas is different. When the number of stations in part a is larger, the channel assignment will use smaller channels; conversely, when the number of channel stations in area a is smaller, the channel allocation strategy will be different. The more the number of channels used for channel assignment. Therefore, in the case of limited channel resources, as far as possible to reduce the use of channels, we can increase the number of sites in part a and reduce the number of sites in part b, so as to achieve the lowest interference, so as to achieve signal transmission quality and improve network performance. According to simulation Figures 5 and 6, it can be seen that the more stations in region a, the less channel assignment. Although the difference between the two is not too large, the less channel usage in the process of network communication can not only reduce the cost but also reduce the interference.

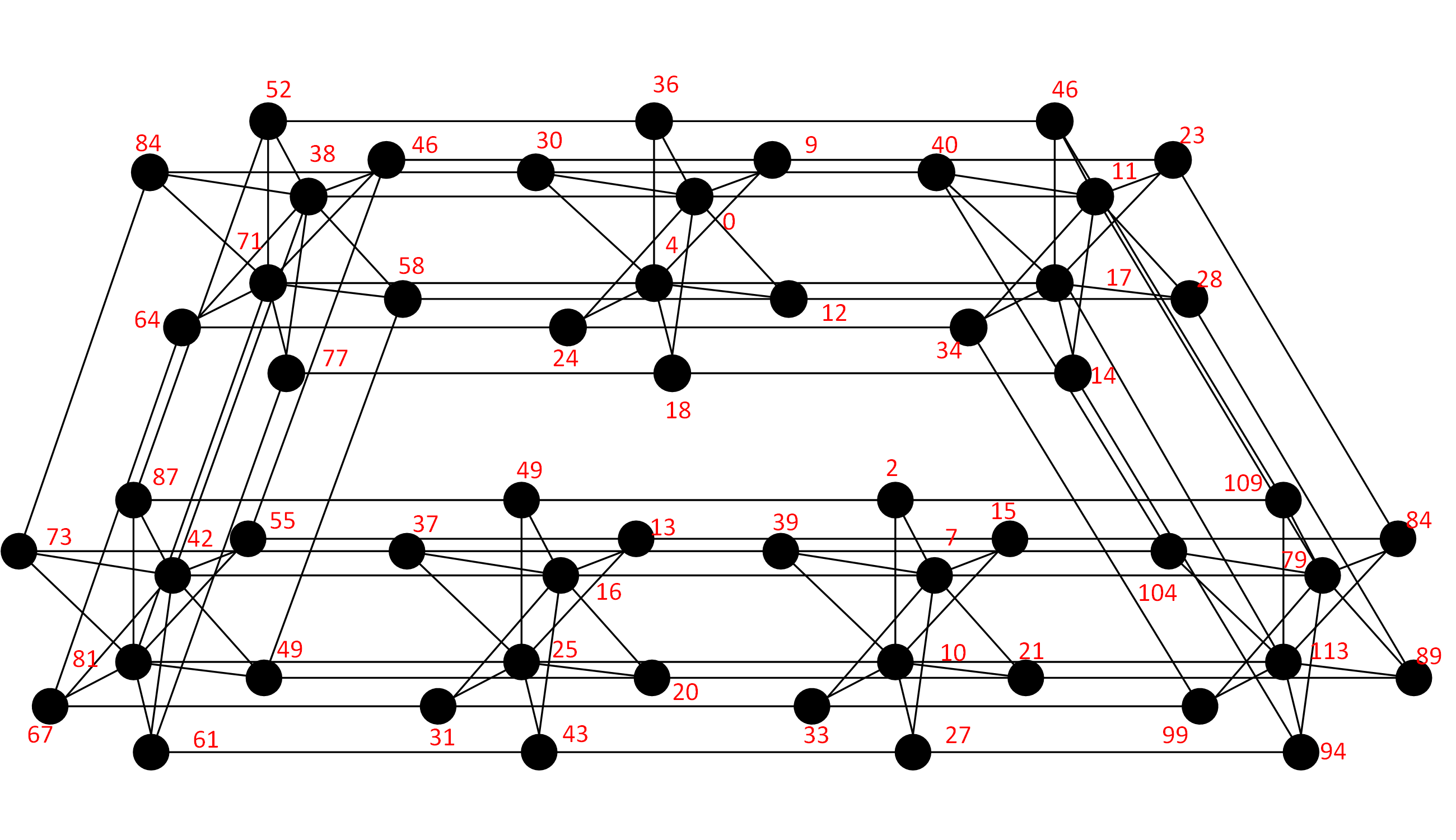
Channel interference refers to the mutual interference between different channels due to the overlap in frequency or time, which will reduce the performance of the network and affect the quality and efficiency of communication. In order to reduce the influence of channel interference, a variety of technical means can be adopted. For example, a channel assignment policy can be used to assign different channels to different users and avoid interference between channels. In addition, interference cancellation technology can also be used to eliminate or reduce channel interference through specific algorithms. In practical application, the influence of channel interference on network can be evaluated by network simulation and test. For example, network simulation software can be used to simulate channel interference and evaluate network performance under different interference conditions. In addition, field tests can be conducted to assess the impact of channel interference on the actual network and optimize the network design based on the test results.

4. Conclusion

In this paper, we mainly determine the lower bounds of the radio number of Cartesian products of complete bipartite graphs and odd cycles, where $m\ge 5$. From the analysis of the number of stations in two parts of a complete bipartite graph, the stations in part a serve as the central vertex, and the more the number in part a, the greater the number of radios. However, in this paper, we only study the lower bound of the radio number of the Cartesian product of this topology, but the radio number of the even cycle as well as its upper bound is still not further investigated.

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under Grant 11551002, in part by the Natural Science Foundation of Qinghai Province under Grant 2019-ZJ-7093; Qinghai normal university in 2024 college students’ innovation and industry training program funded project (qhnucxcy2024021).

Declarations

The authors declare no conflict of interest.