The minimum dominating set problem asks for a dominating set with minimum size. First, we determine some vertices contained in the minimum dominating set of a graph. By applying a particular scheme, we ensure that the resulting graph is 2-connected and the length of each formed induced cycle is 0 mod 3. We label every three vertices in the induced cycles of length 0 mod 3. Then there is a way of labeling in which the set of all labeled vertices is the minimum dominating set of the resulting graph, and is contained in the minimum dominating set of the original graph. We also consider the remaining vertices of the minimum dominating set of the original graph and determine all vertices contained in the minimum dominating set of a graph with maximum degree 3. The complexity of the minimum dominating set problem for cubic graphs was shown to be APX-complete in 2000 and this problem is solved by our arguments in polynomial time.
This paper takes the minimum dominating set problem and aims to determine the minimum dominating set of a cubic graph. A cubic graph is a type of graph where every vertex has degree 3. A dominating set of a graph \(G\) is a set \(S\) of vertices of \(G\) such that every vertex \(v\) of \(G\) is either in \(S\) or adjacent to a vertex of \(S\). A minimum dominating set is a dominating set with minimum size.
Proposition 1.1. [2] A graph is 2-connected if and only if it can be constructed from a cycle by successively adding \(H\)-paths to graphs \(H\) already constructed.
First, we determine some vertices contained in the minimum dominating set of a graph. By applying a particular scheme, we ensure that the resulting graph is 2-connected and the length of each formed induced cycle is 0 mod 3. The scheme has been relaxed from the published paper [3]. We label every three vertices in the induced cycles of length 0 mod 3. Then there is a way of labeling in which the set of all labeled vertices is the minimum dominating set of the resulting graph, and is contained in the minimum dominating set of the original graph. We also consider the remaining vertices of the minimum dominating set of the original graph and determine all vertices contained in the minimum dominating set of a graph with maximum degree 3.
The complexity of the minimum dominating set problem for cubic graphs was shown to be APX-complete [1] and this problem is solved by our arguments in polynomial time, which implies that all NP-complete problems are contained in P.
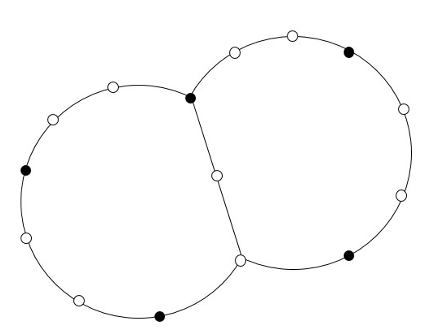
Figure 1 shows an example of the minimum dominating set of a graph with maximum degree 3 derived by the method in this paper.

In this paper, a graph \(G\) is finite, undirected, and simple with the vertex set \(V\) and edge set \(E\). We follow the notations presented in [2]. For a vertex \(v \in V(G)\), the open neighborhood, denoted by \(N_G(v)\), is \(\{ u \in V(G) \colon\ uv \in E(G) \}\), also for a set \(W \subseteq V(G)\), let \(N_G(W) = \bigcup_{v \in W} N_G(v)\) and \(N_G[W] = N_G(W) \cup W\). A dominating set \(X \subseteq V(G)\) is such that \(N_G[X] = V(G)\). A minimum dominating set, called a d-set, is a dominating set with the minimum size. \(X\)-3-path is a path that has labels on the vertices so that the distance between the labels is 3 if the length of the path is at least 2, otherwise \(X\)-3-path is a path of length 1 that has at most one label on the vertices. Two cycles \(C_1\) and \(C_2\) are said to be connecting without seams if \(X\)-3-paths can be assigned to \(C_1\) and \(C_2\) as \(C_1 \cap C_2\) is one \(X\)-3-path.
We consider a connected graph \(G\),
otherwise consider each component one by one. We introduce the
construction scheme \({\bf K}\) as
follows.
\({\bf K}\): Input a connected graph
\(G\).
(1) Let \(G_0 = G\) and \(k = 0\).
(2) If there exists a cut vertex in \(G_k\), then proceed as follows. Let \(v\) be the cut vertex in \(G_k\). For every pair of components \(C_1\) and \(C_2\) of \(G_k – v\) and for every pair of vertices \(v_1 \in C_1 \cap N_{G_k}(v)\) and \(v_2 \in C_2 \cap N_{G_k}(v)\), add an edge \(v_1v_2\) to \(G_k\). Increase \(k\) by \(1\).
(3) Repeat (2) while they occur.
(4) Find an induced cycle in \(G_k\).
(4-1) If it is an induced cycle of length 0 mod 3, assign \(X\)-3-path to it. Increase \(k\) by \(1\).
(4-2) If it is an induced cycle of length 2 mod 3, then proceed as follows. Let \(D_2\) be the induced cycle of length 2 mod 3. Take a 4-path \(Q \subseteq D_2\), and set \(Q = w_1w_2w_3w_4\). Add three edges \(w_1w_3\), \(w_2w_4\), and \(w_1w_4\) to \(G_k\). Assign \(X\)-3-paths to the induced cycles connecting without seams in \(D_2 + w_1w_3 + w_2w_4 + w_1w_4\) (say the subgraph (a)). Increase \(k\) by \(1\).
(4-3) If it is an induced cycle of length 1 mod 3, then proceed as follows. Let \(D_1\) be the induced cycle of length 1 mod 3. Take a 4-path \(Q \subseteq D_1\), and set \(Q = w_1w_2w_3w_4\). Add two edges \(w_1w_3\) and \(w_2w_4\) to \(G_k\). Assign \(X\)-3-paths to the induced cycles connecting without seams in \(D_1 + w_1w_3 + w_2w_4\) (say the subgraph (b)). Increase \(k\) by \(1\).
(5) Find a shortest path \(P\) between two vertices \(v_1\) and \(v_2\) on the previously assigned \(X\)-3-path in \(G_k\) where \(X\)-3-path is not assigned to \({\mathring v_1}P{\mathring v_2}\). Let \(P'\) be the previously assigned \(X\)-3-path with \(v_1\) and \(v_2\) in \(G_k\).
(5-1) If it forms an induced cycle of length 0 mod 3 with \(v_1P'v_2\) in \(G_k\), then proceed as follows. Let \(D_0\) be the induced cycle of length 0 mod 3. Assign \(X\)-3-path to \(D_0\). Increase \(k\) by \(1\).
(5-2) If it forms an induced cycle of length 2 mod 3 with \(v_1P'v_2\) in \(G_k\), then proceed as follows. Let \(D_2\) be the induced cycle of length 2 mod 3. Take a 4-path \(Q \subseteq D_2\), and set \(Q = w_1w_2w_3w_4\). Add three edges \(w_1w_3\), \(w_2w_4\), and \(w_1w_4\) to \(G_k\). Assign \(X\)-3-paths to the induced cycles connecting without seams in \(D_2 + w_1w_3 + w_2w_4 + w_1w_4\) (say the subgraph (a)). Increase \(k\) by \(1\).
(5-3) If it forms an induced cycle of length 1 mod 3 with \(v_1P'v_2\) in \(G_k\), then proceed as follows. Let \(D_1\) be the induced cycle of length 1 mod 3. Take a 4-path \(Q \subseteq D_1\), and set \(Q = w_1w_2w_3w_4\). Add two edges \(w_1w_3\) and \(w_2w_4\) to \(G_k\). Assign \(X\)-3-paths to the induced cycles connecting without seams in \(D_1 + w_1w_3 + w_2w_4\) (say the subgraph (b)). Increase \(k\) by \(1\).
(6) Repeat (5) while they occur.
(7) Return the resulting graph \(G_{k}\).
Let \({\bf K}(G)\) be a graph constructed by applying \({\bf K}\) to \(G\). Note that \({\bf K}(G)\) is not unique and constructed from \(G\) arbitrarily. By the scheme, \({\bf K}(G)\) is 2-connected with \(V(G) = V({\bf K}(G))\) and \(E(G) \subseteq E({\bf K}(G))\), and all edges in \({\bf K}(G)\) should be covered by at least one set of \(X\)-3-paths but may be covered by other set of \(X\)-3-paths with the rotation of labels.
Remark 3.1. Let \(X\) be a dominating set of \(G\). Every subset \(D \subseteq X\) is a d-set of \(G[N_G[D]]\) if and only if \(X\) is a d-set of \(G\).
Consider labeling vertices by assigning \(X\)-3-paths to the induced cycles of length 0 mod 3 connecting without seams in \({\bf K}(G)\) (Figure 2). Note that certain induced cycles are not counted for the labeling, and have as few labeled vertices as possible.
Proposition 3.2. (i) For every labeling, the set of all labeled vertices is a minimal dominating set of \({\bf K}(G)\). In addition, by selecting the first vertex to label, the number of the remaining labeled vertices is uniquely determined. (ii) For at least one labeling, the set of all labeled vertices is a d-set of \({\bf K}(G)\).
Proof. Since every edge in \({\bf K}(G)\) is covered by \(X\)-3-path, for every labeling, the set of all labeled vertices is an independent dominating set of \({\bf K}(G)\), that is, a minimal dominating set of \({\bf K}(G)\). After selecting the vertex to label first, if there are multiple ways to label vertices during the labeling process, those vertices are interchangeable and equivalent. Indeed, those vertices are two adjacent vertices with degree 3 in \(K^{4} – e \subseteq {\bf K}(G)\) for some \(e \in E(K^{4})\). Thus, the number of the remaining labeled vertices is uniquely determined. Therefore, the statement (i) holds. By Remark 3.1, the statement (ii) obviously holds. ◻
Let \(Y\) be a d-set of \({\bf K}(G)\) that is obtained by labeling vertices. Let \(\mathcal{Y}\) be the set of all \(Y\). For \(Y_1, Y_2 \in \mathcal{Y}\), if \(Y_1 \cap Y_2 \ne \emptyset\) and \(Y_1 \setminus Y_2\) has a cut vertex in \(G\), then let \(\mathcal{Y}\) be \(\mathcal{Y} \setminus \{Y_2\}\). Repeat this operation while they occur and let \(\mathcal{A} = \mathcal{Y}\). By the definition of \({\bf K}(G)\), a cut vertex in \(G\) should be labeled rather than its adjacent vertex as we see in Lemma 3.4. For \(A_1, A_2 \in \mathcal{A}\), if \(A_1 \cap A_2 \ne \emptyset\), then let \(A_1\) and \(A_2\) be equivalent and denote \(A_1 \equiv A_2\).
Lemma 3.3. \(\mathcal{A}/\equiv\) is determined in polynomial time and \(|\mathcal{A}/\equiv| \leq |V(G)|\).
Proof. By the definition of \({\bf K}\), \({\bf K}(G)\) is constructed from \(G\) in polynomial time. By the proof of Proposition 3.2 and the definition of \(\mathcal{A}/\equiv\), \(\mathcal{A}/\equiv\) is determined in polynomial time and \(|\mathcal{A}/\equiv| \leq |V(G)|\). ◻
Let \(X\) be a d-set of \(G\). Let \(\mathcal{X}\) be the set of all \(X\).
Lemma 3.4. For some \(\mathcal{B} \in \mathcal{A}/\equiv\) and for each \(Y \in \mathcal{B}\), there exists \(X \in \mathcal{X}\) such that \(Y \subseteq X\).
Proof. Let \(\mathcal{B} \in \mathcal{A}/\equiv\). Consider labeling vertices in \(G \subseteq {\bf K}(G)\). By the definition of \({\bf K}(G)\) and \(\mathcal{B}\), it suffices that considering the subgraph (a) or (b). For any \(Y_1, Y_2 \in \mathcal{B}\) such that \(Y_1 \ne Y_2\), \(N_{{\bf K}(G)}[Y_1 \setminus Y_2] = N_{{\bf K}(G)}[Y_2 \setminus Y_1]\). If \(Y_1\) is a dominating set of \(G\), then for some \(X \in \mathcal{X}\), \(X = Y_1\). Now, \(N_G[Y_2 \setminus Y_1] \setminus N_G[Y_1 \setminus Y_2] \subseteq N_G[Y_1] = V(G)\). By considering the subgraph (a), we have \(N_G[Y_1 \setminus Y_2] \setminus N_G[Y_2 \setminus Y_1] \subseteq N_G[Y_2]\). Hence, \(N_G[Y_1] = N_G[Y_2]\). Suppose that for all \(Y \in \mathcal{A}\), \(Y\) is not a dominating set of \(G\). Now, each \(Y_1\) and \(Y_2\) is not a dominating set of \(G\). By considering the subgraph (b), we have \(N_G[Y_2 \setminus Y_1] \setminus N_G[Y_1 \setminus Y_2] \not \subseteq N_G[Y_1]\) and \(N_G[Y_1 \setminus Y_2] \setminus N_G[Y_2 \setminus Y_1] \not \subseteq N_G[Y_2]\). Hence, \(N_G[Y_1] \setminus N_G[Y_2] \ne \emptyset\) and \(N_G[Y_2] \setminus N_G[Y_1] \ne \emptyset\). Let \(\mathcal{B}_1, \mathcal{B}_2 \in \mathcal{A}/\equiv\) with \(\mathcal{B}_1 \ne \mathcal{B}_2\). For any \(Y_3 \in \mathcal{B}_1\) and any \(Y_4 \in \mathcal{B}_2\), since \(Y_3 \cap Y_4 = \emptyset\) and each \(Y_3\) and \(Y_4\) is not a dominating set of \(G\), it follows that \(N_G[Y_3] \setminus N_G[Y_4] \ne \emptyset\) and \(N_G[Y_4] \setminus N_G[Y_3] \ne \emptyset\). Now, \(Y\) is a d-set of \(G[N_G[Y]]\). Let \(W\) be a subset of \(V(G) \setminus Y\) with minimum size such that \(Y \cup W\) is a dominating set of \(G\). By Remark 3.1, \(Y \cup W\) is a d-set of \(G\). ◻
Suppose that \(Y\) is a d-set of \({\bf K}(G)\) that satisfies Lemma 3.4.
Lemma 3.5. Let \(G'\) be a graph obtained by deleting \(Y\) from, and adding edges to all vertex pairs of \(\bigcup_{y \in Y}N_G(y)\) to \(G\). Let \(Z_1\) be a d-set of \(G'\). Let \(G'' = G – N_G[Y]\) and \(Z_2\) be a d-set of \(G''\). If \(|Z_1| < |Z_2|\), then \(Y \cup Z_1\) is a d-set of \(G\), and \(Z_1 \cap \bigcup_{y \in Y}N_G(y) \ne \emptyset\). If \(|Z_1| \geq |Z_2|\), then \(Y \cup Z_2\) is a d-set of \(G\).
Proof. Obviously, \(Y \cup Z_2\) is a d-set of \(G\) if \(|Z_1| \geq |Z_2|\). For a set \(A \subseteq V(G)\), suppose that \(Y \cup A\) is a d-set of \(G\). Let \(A' = A \setminus N_G[Y]\). Suppose that \(|Z_1| < |Z_2|\). Now, \(A'\) is not a dominating set of \(G''\), and \(A \cap \bigcup_{y \in Y}N_G(y) \ne \emptyset\). By the definition of \(G'\), it suffices that \(A = Z_1\). ◻
Theorem 3.6. The d-set of a graph \(G\) with maximum degree 3 is determined in polynomial time.
Proof. By Lemma 3.4, for some \(X \in \mathcal{X}\), \(Y \subseteq X\). Let \(G\) be a graph with maximum degree 3 and let \(G_0 = G\). Let \(G_1\) be constructed by deleting \(Y\), and for every pair \(w_1, w_2 \in \bigcup_{y \in Y}N_{G_0}(y)\), adding an edge \(w_1w_2\) to \(G_0\). Let \(G_2 = G_0 – N_{G_0}[Y]\). Let \(W_1\) be a d-set of \(G_1\) and \(W_2\) be a d-set of \(G_2\). Since \(G_0\) is a graph with maximum degree 3 and by the definition of \(G_2\), each component of \(G_2\) is a path or cycle, or \(G_2 = \emptyset\). Indeed, each component of \(G_2\) does not have a vertex of degree 3 in its subgraph. Thus \(W_2\) is determined in polynomial time. Suppose that \(|W_1| < |W_2|\). Let \(Y_1\) be a d-set of \({\bf K}(G_1)\) that satisfies Lemma 3.4. By the definition of \(Y_1\), it suffices that \(Y_1 \cap \bigcup_{y \in Y}N_{G_0}(y) \ne \emptyset\). Let \(G_3\) be constructed by deleting \(Y_1\), and for every pair \(w_1, w_2 \in \bigcup_{y \in Y_1}N_{G_1}(y)\), adding an edge \(w_1w_2\) to \(G_1\). Let \(G_4 = G_1 – N_{G_1}[Y_1]\). Let \(W_3\) be a d-set of \(G_3\) and \(W_4\) be a d-set of \(G_4\). By the definition of \(G_4\), each component of \(G_4\) is a path, or \(G_4 = \emptyset\). Thus \(W_4\) is determined in polynomial time. Suppose that \(|W_3| < |W_4|\). Let \(Y_2\) be a d-set of \({\bf K}(G_3)\) that satisfies Lemma 3.4. By the definition of \(Y_2\), it suffices that \(Y_2 \cap \bigcup_{y \in Y_1}N_{G_1}(y) \ne \emptyset\). Let \(G_5\) be constructed by deleting \(Y_2\), and for every pair \(w_1, w_2 \in \bigcup_{y \in Y_2}N_{G_3}(y)\), adding an edge \(w_1w_2\) to \(G_3\). Let \(G_6 = G_3 – N_{G_3}[Y_2]\). Let \(W_5\) be a d-set of \(G_5\) and \(W_6\) be a d-set of \(G_6\). By the definition of \(G_6\), \(V(G_6)\) is independent, or \(G_6 = \emptyset\). Thus \(W_6 = V(G_6)\). Suppose that \(|W_5| < |W_6|\). Let \(Y_3\) be a d-set of \({\bf K}(G_5)\) that satisfies Lemma 3.4. By the definition of \(Y_3\), it suffices that \(Y_3 \cap \bigcup_{y \in Y_2}N_{G_3}(y) \ne \emptyset\). Now, \(Y_3\) is a dominating set of \(G_5\) and so it suffices that \(W_5 = Y_3\). By Lemma 3.3, \(Y_3\) is determined in polynomial time. By Lemma 3.5, if \(|W_5| < |W_6|\), then it suffices that \(W_3 = Y_2 \cup W_5\), otherwise, it suffices that \(W_3 = Y_2 \cup W_6\). By Lemma 3.3, \(Y_2\) is determined in polynomial time. By Lemma 3.5, if \(|W_3| < |W_4|\), then it suffices that \(W_1 = Y_1 \cup W_3\), otherwise, it suffices that \(W_1 = Y_1 \cup W_4\). By Lemma 3.3, \(Y_1\) is determined in polynomial time. By Lemma 3.5, if \(|W_1| < |W_2|\), then it suffices that \(X = Y \cup W_1\), otherwise, it suffices that \(X = Y \cup W_2\). By Lemma 3.3, \(Y\) is determined in polynomial time. Thus, \(X\) is determined in polynomial time. The proof is completed. ◻