Let \( S \) be a connected union of finitely many \( d \)-dimensional boxes in \( \mathbb{R}^d \) and let \( \mathcal{B} \) represent the family of boxes determined by facet hyperplanes for \( S \), with \( \mathcal{F} \) the associated family of faces (including members of \( \mathcal{B} \)). For set \( F \) in \( \mathcal{F} \), point \( x \) relatively interior to \( F \), and point \( y \) in \( S \), \( x \) sees \( y \) via staircase paths in \( S \) if and only if every point of \( F \) sees \( y \) via such paths. Thus the visibility set of \( x \) is a union of members of \( \mathcal{F} \), as is the staircase kernel of \( S \). A similar result holds for \( k \)-staircase paths in \( S \) and the \( k \)-staircase kernel of \( S \).
We begin with a brief overview of the problem. Precise definitions for our terms appear in Section 2. Many results in convexity that involve the usual notion of visibility via straight line segments have interesting analogues that instead use the concept of visibility via staircase paths. Using a familiar example, the Krasnosel’skii theorem [10] says that, for \(S\) a nonempty compact set in \(\mathbb R^2\), \(S\) is starshaped via segments if and only if every three points of \(S\) see via segments in \(S\) a common point. In the staircase analogue [2], for \(S\) a nonempty simply connected orthogonal polygon in \(\mathbb R^2\), \(S\) is staircase starshaped if and only if every two of its points see via staircase paths in \(S\) a common point. Moreover, an interesting study by Chepoi [7] generalizes the planar result to any finite union of boxes in \(\mathbb R^d\) whose corresponding intersection graph is a tree. As he observes, every simply connected orthogonal polygon may be expressed as such a union. (Similarly, non simply connected orthogonal polygons cannot satisfy Chepoi’s requirement.) Appropriately, the staircase kernel for a simply connected orthogonal polygon will be staircase convex [1]. In [6], the results are extended to \(k\)-staircase paths.
Unfortunately, there are not too many satisfying results for an orthogonal polytope \(S\) whose boxes are not so well arranged. (That is, when the boxes for \(S\) cannot be selected to satisfy Chepoi’s restriction.) We do know that the staircase kernel of an orthogonal polygon in \(\mathbb R^2\) need not be connected, although its components will be staircase convex [5]. In addition, results by Pape and Vassilev [13] produce an algorithm for computing the staircase kernel of an orthogonal polygon with holes. In \(\mathbb R^d\), \(d \geq 3\), an example reveals that even a connected staircase kernel for an orthogonal polytope need not be staircase convex [1]. Some results in [4] concern the staircase kernel for an orthogonal polytope whose complement contains open boxes. And results in [3] investigate the staircase kernel of an orthogonal polytope \(S\), using a suitable family of boxes whose union is \(S\) and the vertices of these boxes.
In this paper, we use a smaller family \(\mathcal F\) of boxes to recognize the staircase kernel of an orthogonal polytope \(S\). For a box \(F\) in \(\mathcal F\), the visibility set for any relative interior point \(x\) of \(F\) will determine the visibility set for every point of \(F\), providing a convenient tool to examine the staircase kernel and the staircase \(k\)-kernel for our set. The results have potential applications to computing problems concerning visibility and visibility graphs as well.
This section includes some definitions and notation from [4] and [6]. A set \(B\) in \(\mathbb R^d\) is called a box if and only if \(B\) is a convex polytope (possibly degenerate) whose edges are parallel to the coordinate axes. A nonempty set \(S\) in \(\mathbb R^d\) is an orthogonal polytope if and only if \(S\) is a connected union of finitely many boxes. An orthogonal polytope in the plane is an orthogonal polygon. Let \(\lambda\) be a simple polygonal path in \(\mathbb R^{d}\) whose edges are parallel to the coordinate axes. That is, let \(\lambda\) be a simple rectilinear path in \(\mathbb R^{d}\). For points \(x\) and \(y\) in \(S\), the path \(\lambda\) is called an \(x – y\) path in \(S\) if and only if \(\lambda\) lies in \(S\) and has endpoints \(x\) and \(y\). The \(x – y\) path \(\lambda\) is a staircase path (or simply a staircase) if and only if, as we travel along \(\lambda\) from \(x\) to \(y\), no two edges of \(\lambda\) have opposite directions. That is, for each standard basis vector \(e_i, 1 \leq i \leq d\), either each edge of \(\lambda\) parallel to \(e_i\) is a positive multiple of \(e_i\) or each edge of \(\lambda\) parallel to \(e_i\) is a negative multiple of \(e_i\). Staircase paths \(\lambda\) and \(\mu\) are compatible if and only if no two of their edges have opposite directions.
For points \(x\) and \(y\) in a set \(S\), we say that \(x\) sees \(y\) (\(x\) is visible from \(y\)) via staircase paths if and only if \(S\) contains an \(x-y\) staircase path. For \(x\) fixed in \(S\), the collection \(\{ y \, : \, x\) sees \(y\) via staircase paths in \(S \}\) is called the visibility set of x in \(S\). A set \(S\) is staircase convex (orthogonally convex) if and only if, for every pair of points \(x\), \(y\) in \(S\), \(x\) sees \(y\) via staircase paths. Similarly, a set \(S\) is staircase starshaped (orthogonally starshaped) if and only if, for some point \(p\) in \(S\), \(p\) sees each point of \(S\) via staircase paths. The set of all such \(p\) is the staircase kernel of \(S\), Ker \(S\).
We may extend the notion of a staircase path to a \(k\)-staircase path: For points \(x\) and \(y\) in a set \(S\) and for an \(x – y\) path \(\lambda\) in \(S\), we say that \(\lambda\) is a \(k\)–staircase path in \(S\) if and only if \(\lambda\) is a union of \(k\) (or possibly fewer) staircase paths, \(k \geq 1\). When \(\lambda\) is a \(k\)-staircase path and \(k \geq 2\), we may write \(\lambda=\lambda_1 \cup \cdots \cup \lambda_k\), where each \(\lambda_i\) is a staircase path, \(1 \leq i \leq k\). We assume that consecutive paths \(\lambda_i\) and \(\lambda_{i+1}\) share a unique point for \(1 \leq i \leq k-1\) and that nonconsecutive paths are disjoint. Then in a natural way, we may adapt each of the earlier definitions concerning visibility via staircase paths to visibility via \(k\)-staircase paths. (See [6] for details.)
Throughout the paper, we use the following notation and terminology. For \(S\) any set in \(\mathbb R^d\), int \(S\), rel int \(S\), bdry \(S\), and aff \(S\) will represent the interior, the relative interior, the boundary, and the affine hull, respectively, of set \(S\). For convenience, any vector parallel to a standard basis vector for \(\mathbb R^d\) is called a coordinate vector. Similarly, for every \(i\), \(1 \leq i \leq d\), the hyperplane \(J(i)=\{ (x_1, \ldots , x_d) \, : \, x_i=0\}\) as well as any hyperplane parallel to \(J(i)\) is called a coordinate hyperplane. Any projection from \(\mathbb R^d\) into a coordinate hyperplane will be a coordinate projection, or an orthogonal projection. Finally, if \(\lambda\) is a simple path containing points \(a\) and \(b\), then \(\lambda(a,b)\) will denote the subpath of \(\lambda\) from \(a\) to \(b\). Readers may refer to Valentine [12], to Lay [11], to Danzer, Grünbaum, Klee [8], to Eckhoff [8], and to Hansen, Herburt, Martini, and Moszyńska [9] for discussions concerning straight line segments, starshaped sets, and their applications.
The following definitions will be useful.
Definition 3.1. 1Let \(S\) be a connected union of finitely many boxes in \(\mathbb R^d\), each of which is fully d-dimensional. A hyperplane \(H\) is called a facet hyperplane for \(S\) if and only if \(H \cap (\text{bdry }S)\) contains a fully \((d-1)\)-dimensional box \(F\). If \(F\) is maximal, we call \(F\) a facet of \(S\).
Definition 3.2. Let \(\mathcal{H}\) represent the collection of facet hyperplanes for \(S\). In a natural way, \(\mathcal{H}\) determines a collection \(\mathcal B\) of fully \(d\)-dimensional boxes \(B\) whose union is \(S\) such that, for every box \(B\) in \(\mathcal B\) and every hyperplane \(H\) in \(\mathcal{H}\), \(H \cap (\text{int }B)=\emptyset\). Hence distinct boxes share no interior points.
For each box \(B\) in \(\mathcal B\), we define \(d\) distinct tubes at \(B\). Let \(F_i, F_i^\prime\) represent a pair of parallel facets of \(B\), \(1 \leq i \leq d\), with coordinate vector \(e_i\) orthogonal to these facets. The translates of \(B\) through multiples of \(e_i\) will generate a tube at \(B\). Precisely, the set \(T_i=\cup \{ se_i+b \,: \, s\) a scalar, \(b\) a vector in \(B \}\), is a tube at \(B\), and there are exactly \(d\) such tubes, one for each \(i\), \(1 \leq i \leq d\).
We establish two helpful lemmas for the orthogonal polytope \(S\) above.
Lemma 3.3. Let the orthogonal polytope \(S\) be a union of fully \(d\)-dimensional boxes in \(\mathbb R^d\), with \(\mathcal B\) the corresponding family of boxes determined by facet hyperplanes in our definitions above. Let \(B\) be any box in \(\mathcal B\), \(T\) any tube at \(B\), with \(x\) in int \(B\) and y in int \(T\). If \(x\) sees \(y\) via staircase paths in \(S\), then for every point \(w\) in \(B\), \(w\) also sees \(y\) via staircase paths in \(S\). Clearly these paths lie in tube \(T\).
Proof. Since the visibility set of \(y\) in set \(S\) is closed, it suffices to consider the case for \(w\) in int \(B\). If \(y \in B\), the result is immediate, so assume that \(y\) lies strictly beyond facet \(F\) of \(B\) and in the corresponding tube \(T\). Let \(F^\prime\) be the translate of \(F\) parallel to \(F\) at \(y\) and in this tube. Observe that the interior of the box \(C\) with facets \(F\) and \(F^\prime\) cannot contain points from any facet of \(S\): Certainly no facet hyperplane can meet int \(B\) (by the definition of box \(B\)). Hence any facet of \(S\) meeting int \(C\) would be parallel to \(F\) and \(F^\prime\) and would necessarily extend across the box, separating \(x\) from \(y\) and making it impossible for \(x\) to see \(y\) via staircases in \(S\). Hence int \(C\) and \(C\) itself must lie in \(S\). We conclude that the box \(B \cup C\) lies in \(S\), and \(w\) sees \(y\) via staircases in \(S\). Clearly this staircase lies in tube \(T\), finishing the proof. ◻
Lemma 3.4. Let the orthogonal polytope \(S\) be a union of fully \(d\)-dimensional boxes in \(\mathbb R^d\), with \(\mathcal B\) the corresponding family of boxes determined by facet hyperplanes in our definitions above. For \(B\) any box in \(\mathcal B\), let \(J\) and \(J^\prime\) represent distinct hyperplanes orthogonal to coordinate vector \(e\) and supporting box \(B\), and let hyperplane \(J_0\) be parallel to \(J\) and \(J^\prime\) and between them. (That is, in the region \(A\) whose boundary is \(J\cup J^\prime\).) For \(x\) and \(u\) interior to \(A\), let \(\lambda(x,u)\) be a staircase path. If \(\lambda(x,u)\) lies in \(S\), then the orthogonal projection of \(\lambda(x,u)\) onto \(J_0\) will lie in \(S\) also.
Proof. For the moment assume that \(J_0\) is interior to \(A\). By our definition of box \(B\), no facet hyperplane for \(S\) and parallel to \(J\) may lie in int \(A\). Thus facets of \(S\) either are disjoint from int \(A\) or extend across it, intersecting both \(J\) and \(J^\prime\). Since \(\lambda(x,u)\) avoids such facets, so must translates of \(\lambda(x,u)\) in the direction of \(e\) or \(-e\) and in int \(A\). A similar statement holds for translates of subpaths of \(\lambda(x,u)\) and for the orthogonal projection of \(\lambda(x,u)\) onto hyperplane \(J_0\). Since \(S\) is closed, the result extends to \(J\) and \(J^\prime\) as well, finishing the proof of Lemma 3.4. ◻
Theorem 3.5. Let the orthogonal polytope \(S\) be a union of fully \(d\)-dimensional boxes in \(\mathbb R^d\), with \(\mathcal B\) the corresponding family of boxes determined by facet hyperplanes in our definitions above. Let \(B\) be any box in \(\mathcal B\), with \(x\) in int \(B\) and \(y\) in \(S\). If \(x\) sees \(y\) via staircase paths in \(S\), then for every point \(w\) in \(B\), \(w\) also sees \(y\) via staircase paths in \(S\).
Proof. As in the proof of Lemma 3.3, it suffices to consider the case for \(w\) in int \(B\). If \(y\) belongs to the interior of a tube at \(B\), then the result follows from Lemma 3.3. Hence we assume that \(y\) is not interior to any tube at \(B\). Let \(\lambda(x,y)\) represent any \(x-y\) staircase in \(S\). Then \(\lambda(x,y)\) has a subpath at \(x\) that lies in some tube \(T\) at \(B\). By Lemma 1, \(w\) sees via staircase paths in \(S\) each point of \(\lambda(x,y) \cap( \text{int } T)\). Furthermore, since the visibility set of \(w\) in \(S\) is closed, \(w\) sees via staircase paths the first point of \(\lambda(x,y)\) in bdry \(T\). Of course, such staircases from \(w\) lie in \(T\). For any point \(z\) in \(\lambda(x,y)\cap T\) seen by \(w\) and for a corresponding staircase \(\mu(w,z)\) in \(S \cap T\), if \(\mu(w,z)\) is compatible with \(\lambda(z,y)\), then their union will produce a \(w-y\) staircase in \(S\), the desired result. Hence from all \(x-y\) staircases in \(S\), we assume that staircase \(\lambda(x,y)\) has been selected so that, for a particular point \(z\) in \(\lambda(x,y)\cap T\) seen by \(w\), the staircases \(\mu(w,z)\) and \(\lambda(z,y)\) have fewest opposing directions \(k\) (from the \(d\) such directions available). Observe that, if we select \(z\) in \((\)bdry \(T) \setminus B\), then \(\mu(w,z)\) and \(\lambda(x,z)\) must agree in at least two directions, one to reach a facet of \(B\) that determines the tube \(T\), one to reach the boundary of \(T\) (not necessarily in this order). Therefore, \(0 \leq k \leq d-2.\) If \(k \geq 1\), then \(d \geq 3\).
We will show that \(k=0\). Assume on the contrary that \(k \geq 1\) to obtain a contradiction. Recall that the \(w-z\) staircase \(\mu(w,z)\) lies in tube \(T\). Since \(k \geq 1\), it follows that \(\mu(w,z)\) must introduce a direction different from those in \(\lambda(x,z)\) and opposing a direction in \(\lambda(z,y)\). For convenience, say that \(\mu(w,z)\) employs such a direction \(-e\). Let \(J\) and \(J^\prime\) represent distinct coordinate hyperplanes orthogonal to \(e\) and supporting box \(B\). There are two cases to consider, depending on the location of \(y\). Either \(y\) lies strictly beyond one of \(J\) or \(J^\prime\), say beyond \(J\), or \(y\) lies in the closed parallel strip having boundary \(J \cup J^\prime\). We consider each possibility.
Case 1. Assume that \(y\) is strictly beyond hyperplane \(J\), and let \(u\) denote the last point of \(\lambda(x,y)\) in \(J\). Since \(\mu(w,z)\) uses the direction \(-e\) while \(\lambda(x,z)\) does not, observe that \(w\) is closer to \(J\) than \(x\) and \(z\) are to \(J\). (See Figure 1.)
Project \(\lambda(x,u)\) orthogonally onto \(J\), and let \(\lambda^\prime(x^\prime, u^\prime)\) represent the projected image, with \(z^\prime\) the image of \(z\) in \(J\). (Of course, \(u^\prime=u\).) For \(\mu(w,z)\) our \(w-z\) staircase in tube \(T\), let \(\mu^\prime(w^\prime,z^\prime)\) denote its orthogonally projected image in \(J\). Certainly \(\lambda^\prime(x^\prime,z^\prime)\) employs only edges in the direction of edges in \(\lambda(x,z)\), although it omits edges in the direction of vector \(e\) orthogonal to \(J\). Thus \([x,x^\prime] \cup \lambda^\prime(x^\prime, z^\prime)\) (ordered from \(x\) to \(z^\prime\)) is a staircase whose edges use exactly the directions used by \(\lambda(x,z)\). By Lemma 2, this staircase lies in \(S\). Similar statements hold for \(\lambda^\prime(z^\prime, u^\prime)\) and \(\lambda(z,u)\). Of course, \(\lambda^\prime(z^\prime, u^\prime)\) uses no edge in the direction of \(e\). Clearly \([x,x^\prime] \cup \lambda^\prime(x^\prime, z^\prime) \cup \lambda^\prime(z^\prime, u^\prime) \cup \lambda(u^\prime, y)\) is an \(x-y\) staircase in \(S\), and \(z^\prime\) belongs to the orthogonal hyperplane \(J\).
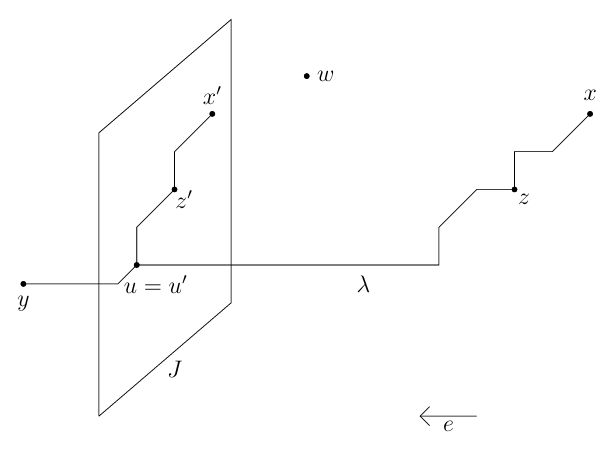
Now examine \(\mu^\prime(w^\prime, z^\prime)\), the orthogonally projected image of \(\mu(w, z)\) in \(J\). This path uses edges whose directions appear in \(\mu(w,z)\) but with one important difference: Any edge of direction \(-e\) has been eliminated. The edge \([w,w^\prime]\) (ordered from \(w\) to \(w^\prime\)) has direction \(e\). Again using Lemma 3.4, \([w, w^\prime] \cup \mu^\prime(w^\prime, z^\prime)\) lies in \(S\). We have in \(S\) new staircase paths \([w, w^\prime] \cup \mu^\prime(w^\prime, z^\prime)\) and \([x,x^\prime] \cup \lambda^\prime(x^\prime, z^\prime) \cup \lambda^\prime(z^\prime, u^\prime) \cup \lambda(u^\prime, y)\), with \(z^\prime\) a point in tube \(T\) seen by \(w\), such that \([w, w^\prime]\cup \mu^\prime(w^\prime, z^\prime)\) and \(\lambda^\prime(z^\prime, u^\prime) \cup \lambda(u^\prime, y)\) use fewer opposing directions then did our original paths \(\mu(w,z)\) and \(\lambda(z,y)\), contradicting our choice of \(\lambda(x,y)\) and \(z\). This finishes Case 1.
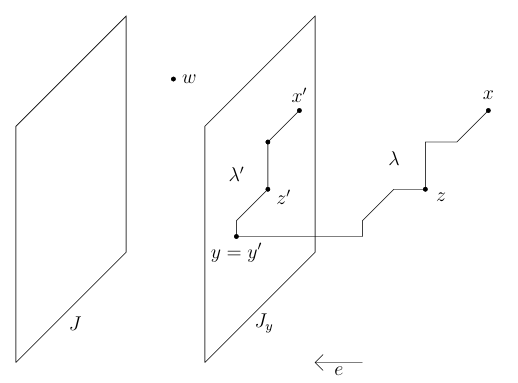
Case 2. Assume that \(y\) is between \(J\) and \(J^\prime\), and let hyperplane \(J_y\) be parallel to \(J\) at \(y\). In case \(w\) and \(z\) are in the same closed halfspace determined by \(J_y\), then since \(\mu(w,z)\) employs direction \(-e\), \(w\) must be closer to \(J_y\) than \(x\) and \(z\) are to \(J_y\). Projecting staircases \(\lambda(x,y)\) and \(\mu(w,z)\) orthogonally onto \(J_y\)and using an argument like the one in Case 1 above, we contradict our choice of \(\lambda(x,y)\) and corresponding \(z\).
Thus we assume that \(w\) and \(z\) lie in opposite open halfspaces determined by \(J_y\). (See Figure 2.) Let \(\lambda^\prime(x^\prime,y^\prime)\) represent the orthogonal projection of \(\lambda(x,y)\) onto \(J_y\), with \(z^\prime\) the image of \(z\) in \(J_y\) and \(y^\prime=y\). Then \([x,x^\prime]\cup \lambda^\prime(x^\prime, y^\prime)=[x,x^\prime] \cup \lambda^\prime(x^\prime, z^\prime)\cup \lambda^\prime(z^\prime, y^\prime)\) is an \(x-y\) staircase in \(S\), with \(z^\prime\) in \(T\). Using Lemma 3.3, we let \(\delta(w,z^\prime)\) represent a \(w-z^\prime\) staircase in \(T\). Clearly \(\delta(w,z^\prime)\) uses only directions from our \(w-z\) staircase \(\mu(w,z)\), including the direction \(-e\). Of course, \(\lambda^\prime(z^\prime, y^\prime)\) lies \(J_y\), uses directions from \(\lambda(z, y)\), but uses neither direction \(e\) nor direction \(-e\). Thus \(\delta(w,z^\prime)\) and \(\lambda^\prime(z^\prime, y)\) exhibit fewer opposing directions than did our original paths \(\mu(w,z)\) and \(\lambda(z,y)\). Again we have contradicted our choice of \(\lambda(x,y)\) and \(z\), finishing Case 2.
In each of the two cases above, our assumption that \(k \geq 1\) has led to a contradiction. Our assumption that \(k \geq 1\) must be false, and we conclude that \(k=0\). Thus \(\mu(w,z)\) is compatible with \(\lambda(z,y)\), and their union \(\mu(w,z)\cup \lambda(z,y)\) yields a \(w-y\) staircase in \(S\). Hence if one point \(x\) of \(\text{int }B\) sees \(y\) via staircase paths in \(S\), the every point of \(B\) sees \(y\) via staircase paths in \(S\), finishing the proof of the theorem. ◻
Our first corollary extends Theorem 3.5 to faces of boxes in family \(\mathcal B\).
Corollary 3.6. Let the orthogonal polytope \(S\) be a union of fully \(d\)-dimensional boxes in \(\mathbb R^d\), with \(\mathcal B\) the corresponding family of boxes determined by facet hyperplanes. Let \(B\) be any box in \(\mathcal B\), with \(F\) a face of \(B\) (possibly \(B\) itself), \(x\) in rel int \(F\), and \(y\) in \(S\). If \(x\) sees \(y\) via staircase paths in \(S\), then every point \(w\) of \(F\) sees \(y\) via staircase paths in \(S\).
Proof. If dim \(F=d\), then \(F\) is box \(B\) in \(\mathcal B\), and the result follows from Theorem 3.5. Hence assume that dim \(F=m<d\), and assume that the result is true for faces of dimension larger than \(m\). As in the proof of Theorem 1, we may assume that \(w\) belongs to rel int \(F\). Let \(\lambda(x,y)\) represent an \(x-y\) staircase in \(S\). If \(\lambda(x,y)\) intersects the relative interior of a face \(G\) of \(B\) for which \(F\) is a proper subface, then the result is immediate by our choice of \(m\). Similarly, if \(\lambda(x,y) \cap B\) contains points of \(B \smallsetminus F\), then \(\lambda(x,y)\cap B\) may be replaced by a staircase path meeting the relative interior of such a face \(G\), and again the result is immediate. Thus we assume that \(\lambda(x,y)\cap B \subseteq F\).
Adapting our earlier argument in Theorem 3.5, the result is true if \(y\) belongs to aff \(F\). For \(y \notin\) aff \(F\), observe that \(\lambda(x,y) \cap (\) aff \(F)\) uses at most \(m\) directions, each represented by a coordinate vector in flat aff \(F\). Let \(v\) represent the last point of \(\lambda(x,y)\) in aff \(F\). Since \(x\) sees \(v\) via staircase \(\lambda(x,v)\) in \(S\), it follows that \(w\) sees \(v\) via staircases in \(S\), and we let \(\mu(w,v)\) represent such a staircase. Clearly \(\mu(w,v) \subseteq\) aff \(F\).
In case the staircases \(\mu(w,v)\) and \(\lambda(v,y)\) are compatible, then the argument is finished. Otherwise, as in the proof of Theorem 3.5, assume that our paths have been selected to minimize the pairs of opposing edges. For appropriate coordinate vectors \(e\) and \(-e\), \(\mu(w,v)\) employs a vector in the direction of \(-e\) while \(\lambda(v,y)\) employs a vector in the direction of \(e\). Let \(J\) and \(J^\prime\) represent distinct hyperplanes supporting box \(B\) and orthogonal to \(e\). Let \(J_v\) denote the hyperplane parallel to \(J\) at \(v\). Then \(w\) and \(y\) must lie in the same open halfspace determined by \(J_v\), while \(x\) belongs to the opposite closed halfspace. (Hence \(J_v\) intersects face \(F\) of \(B\).)
If \(w\) is at least as close to \(J_v\) as \(y\) is to \(J_v\), let \(J_w\) be the hyperplane parallel to \(J\) at \(w\). Let \(u\) be the first point of \(\lambda(x,y)\) in \(J_w\), and project \(\lambda(x,u)\) orthogonally onto \(J_w\). Using an argument in the proof of Theorem 3.5, we obtain a new point \(v^\prime\) in \((\)aff \(F)\cap J_w\) and new paths from \(w\) to \(v^\prime\) and from \(v^\prime\) to \(y\) such that the new paths have fewer opposing directions than the original paths. If \(w\) is farther from \(F_v\) than \(y\) is from \(F_v\), let \(J_y\) be the hyperplane parallel to \(J\) at \(y\). Project \(\lambda(x,y)\) orthogonally into \(J_y\), obtaining a new point \(v^\prime\) in \((\)aff \(F) \cap J_y\) and corresponding new paths such that the new paths have fewer opposing directions than the original paths. Finally, using our argument from the concluding remarks in Theorem 3.5, this finishes the proof of Corollary 3.6. ◻
We may use Theorem 3.5 and Corollary 3.6 to recognize the staircase kernel of an orthogonal polytope.
Corollary 3.7. Let the orthogonal polytope \(S\) be a union of fully \(d\)-dimensional boxes in \(\mathbb R^d\), with \(\mathcal B\) the corresponding family of boxes determined by facet hyperplanes and \(\mathcal F\) the associated family of faces (including members of \(\mathcal B\)). For \(F\) in \(\mathcal F\), \(F\) is a subset of the staircase kernel Ker \(S\) if and only if some point of rel int \(F\) belongs to Ker \(S\).
Finally, it is easy to extend our results to \(k\)-staircase paths.
Corollary 3.8. Let the orthogonal polytope \(S\) be a union of fully \(d\)-dimensional boxes in \(\mathbb R^d\), with \(\mathcal B\) the corresponding family of boxes determined by facet hyperplanes and \(\mathcal F\) the associated family of faces (including members of \(\mathcal B\)). For set \(F\) in \(\mathcal F\), point \(x\) in rel int \(F\), and \(y\) in \(S\), if \(x\) sees \(y\) via \(k\)-staircase paths in \(S\), then every point \(w\) of \(F\) sees \(y\) via \(k\)-staircase paths in \(S\). Thus the \(k\)-staircase kernel of \(S\), if nonempty, is a union of members of \(\mathcal F\).
Proof. It suffices to show that, for \(k \geq 2\), \(w\) sees \(y\) via \(k\)-staircase paths in \(S\). For any \(k\)-staircase path \(\lambda(x,y)\) in \(S\), select \(y^\prime\) in \(\lambda(x,y)\) such that \(x\) sees \(y^\prime\) via staircases in \(S\) and \(y^\prime\) sees \(y\) via \((k-1)\)-staircases in \(S\). By Corollary 3.6, \(w\) sees \(y^\prime\) via staircases in \(S\) and hence sees \(y\) via \(k\)-staircases, finishing the argument. ◻
1. Using the notation above, notice that distinct boxes in \(\mathcal F\) may induce the same visibility sets. In particular, this will hold for members of \(\mathcal F\) that contribute to the kernel of our set.
2. Potential applications of these results include the development of algorithms to determine the staircase kernel or the \(k\)-staircase kernel of an orthogonal polytope in \(\mathbb R^d\).