An outer independent double Roman dominating function (OIDRDF) of a graph \( G \) is a function \( f:V(G)\rightarrow\{0,1,2,3\} \) satisfying the following conditions:
(i) every vertex \( v \) with \( f(v)=0 \) is adjacent to a vertex assigned 3 or at least two vertices assigned 2;
(ii) every vertex \( v \) with \( f(v)=1 \) has a neighbor assigned 2 or 3;
(iii) no two vertices assigned 0 are adjacent.
The weight of an OIDRDF is the sum of its function values over all vertices, and the outer independent double Roman domination number \( \gamma_{oidR}(G) \) is the minimum weight of an OIDRDF on \( G \). Ahangar et al. [Appl. Math. Comput. 364 (2020) 124617] established that for every tree \( T \) of order \( n \geq 4 \), \( \gamma_{oidR}(T)\leq\frac{5}{4}n \) and posed the question of whether this bound holds for all connected graphs. In this paper, we show that for a unicyclic graph \( G \) of order \( n \), \( \gamma_{oidR}(G) \leq \frac{5n+2}{4} \), and for a bicyclic graph, \( \gamma_{oidR}(G) \leq \frac{5n+4}{4} \). We further characterize the graphs attaining these bounds, providing a negative answer to the question posed by Ahangar et al.
Throughout this paper, \(G\) is a simple graph with vertex set \(V(G)\) and edge set \(E(G)\) (briefly \(V,E\)). The order \(|V|\) of \(G\) is denoted by \(n=n(G)\). For every vertex \(v\in V(G)\), the open neighborhood of \(v\) is the set \(N_{G}(v)=N(v)=\{u\in V(G)\mid uv\in E(G)\}\) and the degree of \(v\in V\) is \(\deg(v)=|N(v)|\). A leaf of \(G\) is a vertex with degree one while a support vertex is a vertex adjacent to a leaf. A support vertex is strong if it has at least two leaf neighbors. We denote by \(L(v)\) the set of all leaves adjacent to a vertex \(v\) and by \(L(G)\) the set of leaves of \(G.\)
A path and a cycle of order \(n\) are denoted by \(P_{n}\) and \(C_{n}\), respectively. The corona \(cor(H)\) of a graph \(H\) is the graph obtained from \(H\) by adding for each vertex \(v\in V(H)\) a new vertex \(v^{\prime}\) and the edge \(vv^{\prime}\). A graph \(G\) is called a cactus graph if each edge of \(G\) belongs to at most one cycle. A connected cactus graph is a tree if it has no cycle, a unicyclic if it has exactly one cycle and it is bicyclic if it has two cycles.
A double Roman dominating function, abbreviated DRDF, on a graph \(G\) is a function \(f:V\rightarrow\{0,1,2,3\}\) having the property that if \(f(v)=0\), then vertex \(v\) has at least two neighbors assigned 2 or one neighbor assigned 3 under \(f\), and if \(f(v)=1\), then vertex \(v\) has at least one neighbor assigned 2 or 3. Double Roman domination was introduced in 2016 by Beeler et al. [2], and has been widely studied ever since. For further details on this concept, we refer the reader to book chapter of Chellali et al. [3] and the survey paper of Poklukar and Žerovnik [5]. The complexity of double Roman domination has been studied in [6].
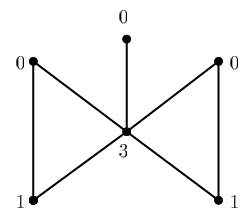
In this paper, we are interested in a variation of double Roman domination introduced in 2020 by Ahangar et al. [1]. An outer independent double Roman dominating function \(f\), abbreviated OIDRDF, on a graph \(G\) is a DRDF such that no two vertices assigned 0 under \(f\) are adjacent. The weight of an OIDRDF is the sum of its function values over all vertices, and the outer independent double Roman domination number \(\gamma_{oidR}(G),\) abreviated OIDR-domination number, is the minimum weight of an OIDRDF on \(G\). The concept of outer independent double Roman domination was subsequently studied in [4,7,10,8,9]. As an example, the graph depicted in Figure 1 has an OIDR-domination number equal to 5, where the center vertex is assigned 3. But since the set of the remaining vertices in not independent, then one vertex of degree 2 of each triangle is assigned 1, and the three remaining vertices are assigned 0 (see Figure 1). Moreover, it is worth noting that the decision problem associated with \(\gamma_{oidR}(G)\) has been shown to be NP-complete in [1] for bipartite and chordal graphs, while in [4] for planar graphs of degree at most four. Therefore the interest in establishing bounds on this parameter that are easily verified, that is, expressed in terms of the order, maximum degree, minimum degree, etc.
In [1], Ahangar et al. have given an upper bound for the OIDR-domination number of any tree \(T\) of order at least three in terms of the order and number of support vertices.
Theorem 1.1 ([1]). For each tree \(T\) of order \(n\geq3,\)
\[\gamma_{oidR}(T)\leq n+\frac{s(T)}{2},\] where \(s(T)\) is the number of support vertices of \(T\).
Since for any tree \(T\) of order \(n\geq3\), \(s(T)\leq\frac{n}{2}\), the following upper bound has been derived.
Corollary 1.2 ([1]).For each tree \(T\) of order \(n\geq3,\) \(\gamma_{oidR}(T)\leq\frac{5n}{4}\).
Furthermore, the authors [1] raised the question of whether the upper bound in Corollary 1.2 remains valid for every connected graph of order at least four. It is worth noting that a characterization of all trees \(T\) attaining the bound in Corollary 1.2 was given in [7] as follows: let \(\mathcal{T}\) be the family of trees \(T\) obtained from disjoint copies of a path \(P_{4}\) by adding edges between support vertices of paths so that the resulting graph is a tree.
Theorem 1.3([7]).Let \(T\) be a tree on \(n\geq4\) vertices. Then \(\gamma_{oidR}(T)=\frac{5n}{4}\) if and only if \(T\in\mathcal{T}.\)
In this paper, we are interested in establishing an upper bound of the OIDR-number for unicyclic and bicyclic graphs. More precisely, we show that if \(G\) is a connected unicyclic graph of order \(n,\) then \(\gamma_{oidR}% (G)\leq\frac{5n+2}{4}\), while if \(G\) is a connected bicyclic graph, then \(\gamma_{oidR}(G)\leq\frac{5n+4}{4}\). Moreover, we characterize all connected unicyclic and bicyclic attaining the aforementioned bounds, respectively, which therefore provides a negative answer to the previous question asked in [1].
We close this section by a useful result established in [1] that gives the exact value of the OIDR-domination number for paths and cycles.
Proposition 1.4([1]).For \(n\geq3\),
(i) \(\gamma_{oidR}(P_{n})=\left\{ \begin{array} [c]{lll}% n & \mathrm{if} \;\; {n=3,}\\ n+1 & \mathrm{otherwise.}% \end{array} \right.\)
(ii) \(\gamma_{oidR}(C_{n})=\left\{ \begin{array} [c]{ll}% n & \mathrm{if}\text{ }n\text{ }\mathrm{is}\text{ }\mathrm{even,}\\ n+1 & \mathrm{otherwise.}% \end{array} \right.\)
In this section, we present an upper bound on the OIDR-domination number of connected unicyclic graphs, and we characterize the extremal unicyclic graphs attaining this bound. We begin by considering a specific unicyclic graph, namely the corona of a cycle \(C_{t},\) where the exact value of the OIDR-domination number will be provided.
Proposition 2.1. For \(t\geq3\),
\[\gamma_{oidR}(cor(C_{t})) {=} \left\{ \begin{array} [c]{ll}% \frac{5t}{2} & \mathrm{if}\text{ }t\text{ }\mathrm{is}\text{ }\mathrm{even,}\\ & \\ \frac{5t+1}{2} & \mathrm{otherwise.}% \end{array} \right.\]
Proof. Let \(V(C_{t})=\{x_{1},x_{2},\dots,x_{t}\}\) and \(L(cor(C_{t}% ))=\{y_{1},y_{2},\dots,y_{t}\},\) where for each \(i,\) \(y_{i}\) is the leaf neighbor of \(x_{i}.\) Note that \(cor(C_{t})\) has order \(2t.\) First, assume that \(t\) is even and consider the function \(f\) defined by \(f(x_{2i-1})=3,\) \(f(y_{2i})=2\) for \(i=1,\dots,\frac{t}{2},\) and \(f(u)=0\) for any other vertex \(u.\) Obviously, \(f\) is an OIDRDF on \(cor(C_{t})\) of weight \(\frac{5t}{2}.\) Assume now that \(t\) is odd, and consider the function \(g\) defined by \(g(x_{2i-1})=g(x_{t})=3,\) \(g(y_{2i})=2\) for \(i=1,\dots,\frac{t-1}{2},\) and \(g(u)=0\) for any other vertex \(u.\) Obviously, \(g\) is an OIDRDF on \(cor(C_{t})\) of weight \(\frac{5t+1}{2}.\) This proves the upper bound.
To prove the inverse inequality, we use an induction on \(t\). Let \(f\) be a \(\gamma_{oidR}(cor(C_{t}))\) such that \(f(V(C_{t}))\) is as large as possible. First observe that if \(f(x_{i})=1\) for some \(i\), then by definition of an OIDRD-function, \(f(y_{i})=2\), and thus the function \(g\) defined on \(cor(C_{t})\) by \(g(x_{i})=3,g(y_{i})=0\) and \(g(u)=f(u)\) otherwise, is a \(\gamma_{oidR}(cor(C_{t}))\) with more weight on \(V(C_{t}),\) which contradicts the choice of \(f\). Likewise, if \(f(x_{i})=2\) for some \(i\), then the minimality of \(f\) implies that \(f(y_{i})=1,\) and as before reassigning \(x_{i}\) and \(y_{i}\) the values \(3\) an \(0\) provides a \(\gamma_{oidR}(cor(C_{t}))\) that contradicts the choice of \(f.\) Therefore \(f(x_{i})\in\{0,3\}\) for each \(i\). As a result, since \(f\) is an OIDRD-function, if \(f(x_{i})=0,\) then we must have \(f(x_{i-1})=f(x_{i+1})=3\). Now, without loss of generality, assume that \(f(x_{1})=3\), and thus \(f(y_{1})=0.\) If \(t=3\), then \(3\in\{f(x_{2}% ),f(x_{3})\},\) say \(f(x_{2})=3\) and thus \(f(y_{3})=2\) and \(f(x)=0\) for \(x\in\{y_{1},y_{2},x_{3}\}\). Hence \(\gamma_{oidR}(cor(C_{t}))=8=\frac{5t+1}% {2},\) establishing that base step. Let \(t\geq4\) and assume that for any \(t^{\prime}\) with \(3\leq t^{\prime}<t,\) we have \[\gamma_{oidR}(cor(C_{t^{\prime}}))\geq\left\{ \begin{array} [c]{ll}% \frac{5t^{\prime}}{2} & \mathrm{if}\text{ }t^{\prime}\text{ }\mathrm{is}\text{ }\mathrm{even},\\ & \\ \frac{5t^{\prime}+1}{2} & \mathrm{otherwise.}% \end{array} \right.\]
First, let \(t\geq4\) is even. If \(f(x_{i})=f(x_{i+1})=3\) for some \(i\), say \(i=1\), then the restriction of \(f\) to \(cor\left( (C_{t}-\{x_{2}\})+x_{1}% x_{3}\right)\) is an OIDRD-function on \(cor((C_{t}-\{x_{2}\})+x_{1}x_{3}).\) Applying the induction hypothesis on \(cor(C_{t}-\{x_{2}\})+x_{1}x_{3}\) leads to \(\omega(f)\geq\frac{5(t-1)+1}{2}+3=\frac{5t+2}{2}\). Now let \(t\geq5\) is odd. Then we must have \(f(x_{i})=f(x_{i+1})=3\) for some \(i\), say \(i=1\). In this case, the restriction of \(f\) to \(cor\left( (C_{t}-\{x_{2}\})+x_{1}% x_{3}\right)\) is an OIDRD-function on \(cor((C_{t}-\{x_{2}\})+x_{1}x_{3})\) and by the induction hypothesis on the resulting corona, we get \(\omega (f)\geq\frac{5(t-1)}{2}+3=\frac{5t+1}{2}\). In either case, \[\gamma_{oidR}(cor(C_{t}))=\left\{ \begin{array} [c]{ll}% \frac{5t}{2} & \mathrm{if}\text{ }t\text{ }\mathrm{is}\text{ }\mathrm{even},\\ & \\ \frac{5t+1}{2} & \mathrm{otherwise.}% \end{array} \right.\] and the proof is complete. ◻
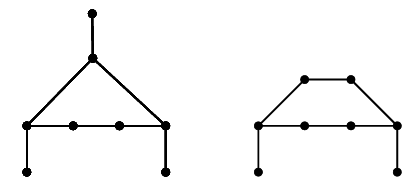
In the following, the graphs \(U_{1}\) and \(U_{2}\) depicted in Figure 2 will be considered in the proof of the main result of this section.
Let \(\mathcal{U}\) be the family of unlabeled unicyclic graphs \(G\) that can be obtained from a sequence \(G_{1},\dots,G_{j}\;(j\geq1)\) of unicyclic graphs such that \(G_{1}=cor(C_{t})\) for some odd \(t\) and, if \(j\geq2\), then \(G_{i+1}\) can be obtained recursively from \(G_{i}\) by the operation \(\mathcal{O}\) below.
Operation \(\mathcal{O}\): Assume that \(u\) is a support vertex of \(G_{i}\). Then \(G_{i+1}\) is obtained from \(G_{i}\) by adding a path \(P_{4}:\) \(w_{1}w_{2}w_{3}w_{4}\) and the edge \(uw_{2}\) (see Figure 3).
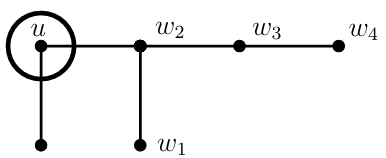
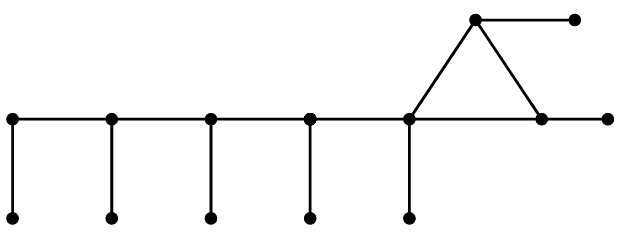
Figure 4 shows a graph obtained from Corona \(C_3\) by applying Operation \(\mathcal O\) twice. The following lemma will useful in what follows, but since its proof is quite simple, we will omit it.
Lemma 2.2. If \(G\in\mathcal{U}\), then \(\gamma_{oidR}(G)=\frac{5n+2}{4}\). Moreover,
(i) for any leaf \(u\) of \(G\) with support vertex \(v\), there exists a \(\gamma_{oidR}(G)\)-function that assigns 2 to \(u\) and \(v\) is doubly Roman dominated by vertices of \(G-u\).
(ii) for any support vertex \(v\) of \(G\), there exists a \(\gamma_{oidR}(G)\)-function that assigns at least 2 to \(v\).
Theorem 2.3. If \(G\) is a connected unicyclic graph of order \(n\), then \[\gamma_{oidR}(G)\leq\frac{5n+2}{4}%\] with equality if and only if \(G\in\mathcal{U}\).
Proof. We use an induction on the order \(n\). It can be seen that for \(n\in\{3,4,5,6,7\},\) \(\gamma_{oidR}(G)\leq\frac{5n+2}{4},\) with equality if and only if \(G=cor(C_{3}),\) establishing the base case. Let \(n\geq8\) and assume that the result holds for all unicyclic graphs of order less than \(n\). Let \(G\) be a unicyclic graph of order \(n\). If \(G\) is a cycle, then by Proposition 1.4, \(\gamma_{oidR}(G)\in\{n,n+1\}\), and thus \(\gamma _{oidR}(G)\leq\frac{5n+1}{4}<\frac{5n+2}{4},\) since \(n\geq8\). Hence we can assume that \(G\neq C_{n},\) and so we must have at least one leaf. Let \(C\) denote the unique cycle of \(G\), and let \(a_{0}\) be a vertex of \(C\) such that \(\deg(a_{0})\) is as maximum as possible. Moreover, let \(a_{0}\dots a_{k}\), with \(k\geq1\), be a path from \(a_{0}\) to a farthest leaf \(a_{k}\) of \(G\), where every \(a_{i}\) is outside \(C\) for \(i\in\{1,\ldots,k\}\). Suppose that \(|V(C)|=m\), and let \(V(C)=\{a_{0},c_{1},c_{2},\ldots,c_{m-1}\}\), where \(m\geq3\), \(a_{0}\) is adjacent to \(c_{1}\) and \(c_{m-1}\), and \(c_{i}\) is adjacent to \(c_{i+1}\) for \(i\in\{1,\ldots,m-2\}\). Before going further, we need to prove the following claim.
Claim 1. If \(x\in C\) is a strong support vertex of degree at least four such that all its neighbors but two are leaves, or \(x\in V(G)-C\) is a strong support vertex such that all its neighbors but one are leaves, then \(\gamma_{oidR}(G)<\frac{5n+2}{4}\).
Proof of Claim 1. Assume first that \(x\in C\) is a strong support vertex of degree at least four such that all its neighbors but two are leaves and let \(x_{1}\) and \(x_{2}\) be the neighbors of \(x\) on \(C\). Consider the graph \(G^{\prime}\) obtained from \(G\) by removing the edges \(xx_{1},xx_{2}\). Clearly, \(G^{\prime}\) has two components, each of which is a tree. Let \(T\) be the component of \(G^{\prime}\) that contains \(x_{1}\) and note that \(|V(T)|\geq2.\) If \(|V(T)|\geq3\), then every \(\gamma_{oidR}(T)\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(x\) and 0 to each leaf neighbor of \(x\). It follows from Theorem 1.1 that \[\gamma_{oidR}(G)\leq\gamma_{oidR}(T)+3\leq\frac{5(n-3)}{4}+3<\frac{5n+2}{4}.\]
Now, if \(|V(T)|=2\), then the function \(f\) defined on \(V(T)\) by \(f(x)=3\), \(f(x_{1})=1\) and \(f(w)=0\) for \(w\in V(G)-\{x,x_{1}\}\), is an OIDRDF of \(G\) of weight \(4\), and clearly, \(\gamma_{oidR}(G)<\frac{5n+2}{4}\).
Assume now that \(x\in V(G)-C\) is a strong support vertex such that all its neighbors but one are leaves. Consider the graph \(G^{\prime}\) obtained from \(G\) by removing \(x\) and all its leaf neighbors. Clearly, \(G^{\prime}\) is unicyclic graph of order at least three, and since every \(\gamma _{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(x\) and 0 to each leaf neighbor of \(x,\) we obtain by applying the induction hypothesis on \(G^{\prime},\) \[\gamma_{oidR}(G)\leq\gamma_{oidR}(G^{\prime})+3\leq\frac{5(n-3)+2}{4}% +3<\frac{5n+2}{4},\] as desired. ◻
For the remainder, consider the following two cases.
Case 1. \(k\geq3\). We first note that by Claim 1, \(a_{k-1}\) has degree two. We distinguish two other situations.
Subcase 1.1. \(\deg(a_{k-2})\geq3\). Suppose that \(a_{k-2}\) has \(q_{1}\) neighbors as support vertices of degree two and \(q_{2}\) neighbors as leaves. Clearly \(q_{1}\geq1\) (because of \(a_{k-1}\)) and \(q_{1}+q_{2}\geq2\) (because of the degree of \(a_{k-2}\)). Let \(G^{\prime}\) be the component of \(G-a_{k-2}\) that contains \(a_{k-3}\) and let \(f^{\prime}\) be a \(\gamma_{oidR}(G^{\prime})\)-function. Note that \(G^{\prime}\) is unicyclic of order at least 3. If \(q_{2}\geq1\), then \(f^{\prime}\) can be extended to an OIDRDF of \(G\) by assigning 3 to \(a_{k-2}\) and 0 to its neighbors with the exception of \(a_{k-3}\), 2 to any other remaining vertex. By the induction hypothesis on \(G^{\prime}\) and since \(q_{1}\geq1\) and \(q_{2}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2q_{1}% +3\nonumber\label{equc1}\\ & \leq\frac{5(n-2q_{1}-q_{2}-1)+2}{4}+2q_{1}+3\nonumber\\ & \leq\frac{5n-2q_{1}-5q_{2}+7+2}{4}\leq\frac{5n+2}{4}. \end{aligned} \tag{1}\]
Further if \(\gamma\)\(_{oidR}(G)=\frac{5n+2}{4}\), then we have equality throughout the inequality chain (1). In particular \(q_{1}=q_{2}=1\) and \(\gamma_{oidR}(G^{\prime})=\frac{5(n-4)+2}{4}\). It follows from the induction hypothesis that \(G^{\prime}\in\mathcal{U}\). If \(a_{k-3}\) is a leaf in \(G^{\prime}\), then by Lemma 2.2, \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime})\) that assigns 2 to \(a_{k-3}\) and \(a_{k-4}\) is doubly Roman dominated by the vertices in \(G^{\prime}-a_{k-3}\). Then reassigning \(a_{k-3}\) a 1 and assigning 3 to \(a_{k-2}\), 2 to \(a_{k}\) and 0 to \(a_{k-1}\) and the leaf neighbor of \(a_{k-2}\), provides an OIDRDF of \(G\) of weight \(\gamma_{oidR}(G^{\prime})+4\) which leads to a contradiction. Thus \(v_{k-3}\) is a support vertex of \(G^{\prime}\) and so \(G\in\mathcal{U}\).
Now, if \(q_{2}=0\), then \(q_{1}\geq2\) and \(f^{\prime}\) can be extended to an OIDRDF of \(G\) by assigning 0 to all neighbors of \(a_{k-2}\) except \(a_{k-3}\) and 2 to any other remaining vertex. By the induction hypothesis on \(G^{\prime}\) and since \(q_{1}\geq2\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2q_{1}+2\\ & \leq\frac{5(n-2q_{1}-1)+2}{4}+2q_{1}+2\\ & \leq\frac{5n-2q_{1}+3+2}{4}\\ & \leq\frac{5n+1}{4}<\frac{5n+2}{4}. \end{aligned}\]
Subcase 1.2. \(\deg(a_{k-2})=2\).
Observe that if \(a_{k-3}\) has a neighbor \(t_{1}\) outside \(C\) such that there is a path \(a_{k-3}t_{1}t_{2}t_{3}\) from \(a_{k-3}\) to a leaf \(t_{3}\), then \(t_{3}\) plays the role of \(a_{k}\) (since \(t_{3}\) is as far from \(a_{0}\) as the vertex \(a_{k}\)). Which leads that \(\deg(t_{1})=\deg(t_{2})=2\). Thus, any neighbor of \(a_{k-3}\) outside \(C\) is a leaf, a support vertex of degree two (because of Claim 1), or a vertex of degree two which is adjacent to a support vertex of degree two. Accordingly, suppose that \(a_{k-3}\) is adjacent to \(h_{1}\) leaves, \(h_{2}\) support vertices of degree two and \(h_{3}\) vertices of degree two each of which is adjacent to a support vertex of degree two, that we recall are all outside \(C.\) Clearly \(h_{3}\geq1,\) because of \(a_{k-2}\).
First, assume that \(k\geq4\). Remove the edge \(a_{k-3}a_{k-4}\) from \(G\) and consider the component \(G^{\prime}\) that contains \(a_{k-4}.\) Note that \(G^{\prime}\) is unicyclic of order at least 3. Let \(f^{\prime}\) be a \(\gamma_{oidR}(G^{\prime})\)-function. If \(h_{1}\geq1\), then \(f^{\prime}\) can be extended to an OIDRDF of \(G\) by assigning 3 to \(a_{k-3}\) and to each support vertex at distance 2 from \(a_{k-3}\), 2 to any leaf at distance two from \(a_{k-3}\) and 0 to any other vertex in \(V(G)-V(G^{\prime})\). By the induction hypothesis on \(G^{\prime}\) and since \(h_{1}\geq1\) and \(h_{3}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3}+3\\ & \leq\frac{5(n-h_{1}-2h_{2}-3h_{3}-1)+2}{4}+2h_{2}+3h_{3}+3\\ & \leq\frac{5n-5h_{1}-2h_{2}-3h_{3}+7+2}{4}\\ & \leq\frac{5n+1}{4}<\frac{5n+2}{4}. \end{aligned}\]
If \(h_{1}=0\), then \(f^{\prime}\) can be extended to an OIDRDF of \(G\) by assigning 3 to each support vertex at distance 2 from \(a_{k-3}\), 2 to \(a_{k-3}\) and any leaf at distance two from it and 0 to any other vertex in \(V(G)-V(G^{\prime})\). By the induction hypothesis on \(G^{\prime}\) and since \(h_{3}\geq1\), we have \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3}% +2\nonumber\label{equc2}\\ & \leq\frac{5(n-2h_{2}-3h_{3}-1)+2}{4}+2h_{2}+3h_{3}+2\nonumber\\ & \leq\frac{5n-2h_{2}-3h_{3}+3+2}{4}\notag\\&\leq\frac{5n+2}{4}. \end{aligned} \tag{2}\]
Further if \(\gamma_{oidR}(G)=\frac{5n+2}{4},\) then we have equality throughout the inequality chain (2). In particular \(h_{3}=1,h_{2}=0\) and \(\gamma_{oidR}(G^{\prime})=\frac{5(n-4)+2}{4}\). By the the induction hypothesis, \(G^{\prime}\in\mathcal{U}\), where \(a_{k-4}\) can be a leaf or a support vertex. But in any case, by items (i) and (ii) of Lemma 2.2, \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime})\)-function \(f^{\prime}\) that assigns at least 2 to \(a_{k-4}\). In this case, assigning 2 to \(a_{k},a_{k-2}\), and 0 to \(a_{k-1},a_{k-3}\), \(f^{\prime}\) can be extended to an OIDRDF of \(G\) of weight \(\gamma_{oidR}(G^{\prime})+4\) which leads to a contradiction. Therefore, the equality does not holds, that is \(\gamma _{oidR}(G)<\frac{5n+2}{4}.\)
Finally, assume that \(k=3\). Remove vertex \(a_{0}\) from \(G,\) and consider \(T\) the component of \(G-a_{0}\) that contains \(c_{1}.\) Note that \(T\) is a tree and has order at least 2. Let \(f^{\prime}\) be a \(\gamma_{oidR}(T)\)-function, and assume first that \(|V(T)|\geq3\). If \(h_{1}\geq1\), then \(f^{\prime}\) can be extended to an OIDRDF of \(G\) by assigning 3 to \(a_{0}\) and to each support vertex (not in \(T\)) at distance 2 from \(a_{0}\), 2 to any leaf (not in \(T\)) at distance two from \(a_{0}\) and 0 to any other vertex in \(V(G)-V(T)\). By Theorem 1.1, and since \(h_{1}\geq1\) and \(h_{3}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(T)+2h_{2}+3h_{3}+3\\ & \leq\frac{5(n-h_{1}-2h_{2}-3h_{3}-1)}{4}+2h_{2}+3h_{3}+3\\ & \leq\frac{5n-5h_{1}-2h_{2}-3h_{3}+7}{4}\\ & {<\frac{5n}{4}.}% \end{aligned}\]
If \(h_{1}=0\), then \(f^{\prime}\) can be extended to an OIDRDF of \(G\) by assigning 3 to each support vertex (not in \(T\)) at distance two from \(a_{0}\), 2 to \(a_{0}\) and to any leaf (not in \(T\)) at distance two from \(a_{0}\) and 0 to any other vertex in \(V(G)-V(T)\). By Theorem 1.1 and since \(h_{3}\geq 1\), we have \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(T)+2h_{2}+3h_{3}+2\\ & \leq\frac{5(n-2h_{2}-3h_{3}-1)}{4}+2h_{2}+3h_{3}+2\\ & \leq\frac{5n-2h_{2}-3h_{3}+3}{4}\\ & {\leq\frac{5n}{4}<\frac{5n+2}{4}.} \end{aligned}\]
Now, let \(|V(T^{\prime})|=2\). Then \(n=3h_{3}+2h_{2}+h_{1}+3\). Define the function \(f\) on \(V(G)\) that assigns 3 to \(a_{0}\) and each support vertex at distance 2 from it, 2 to any leaf at distance two from \(a_{0}\), 1 to \(c_{1}\) and 0 to any other vertex. Obviously, \(f\) is an OIDRDF of \(G\) of weight \(4+3h_{3}+2h_{2}\), and so \(\gamma_{oidR}(G)<\frac{5n+2}{4}\).
Case 2. \(k\in\{1,2\}\).
Note that any neighbor of \(a_{0}\) outside \(C\) is either a leaf or a support vertex of degree two. Let \(h_{1}\) be the number of support vertices outside \(C\) that are adjacent to \(a_{0}\) and let \(h_{2}\) be the number of leaf neighbors of \(a_{0}%\). Consider the following two subcases.
Subcase 2.1. \(\deg(a_{0})\geq4\).
Claim 1 implies that \(k=2\), and thus \(h_{1}\geq1\) and \(h_{1}+h_{2}\geq2\). Let \(T\) be the component of \(G-a_{0}\) that contains \(c_{1}\) and \(f^{\prime}\) be a \(\gamma_{oidR}(T)\)-function. Note that \(T\) is a tree of order at least two. First, let \(|V(T)|\geq3\). If \(h_{2}\geq1\), then \(f^{\prime}\) can be extended to an OIDRDF for \(G\) by assigning 3 to \(a_{0}\), 0 to its neighbors outside \(C\), and 2 to any other remaining vertex. By Theorem 1.1, we have; \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(T)+2h_{1}+3\\ & \leq\frac{5(n-2h_{1}-h_{2}-1)}{4}+2h_{1}+3\\ & =\frac{5n-2h_{1}-5h_{2}+7}{4}\\ & {\leq\frac{5n}{4}<\frac{5n+2}{4}.} \end{aligned}\]
Hence we can assume that \(h_{2}=0,\) and thus \(h_{1}\geq2\). In this case, we extend the function \(f^{\prime}\) to an OIDRDF on \(G\) by assigning 0 to the neighbors of \(a_{0}\) outside \(C\), and 2 to any other remaining vertex (including \(a_{0}\)). It follows from Theorem 1.1 that; \[\gamma_{oidR}(G)\leq\gamma_{oidR}(T)+2h_{1}+2\leq\frac{5(n-2h_{1}-1)} {4}+2h_{1}+2\leq{\frac{5n-1}{4}<\frac{5n+2}{4}.}\]
Assume now that \(|V(T)|=2\). Clearly, \(n=2h_{1}+h_{2}+3.\) Define an OIDRDF on \(V(G)\) of weight \(4+2h_{2}\) as follows: assign 3 to \(a_{0}\), 0 to any neighbor of \(a_{0}\) except \(c_{1}\), 1 to \(c_{1}\) and 2 to any other vertex. It follows that; \[\gamma_{oidR}(G)=4+2h_{1}<\frac{5(2h_{1}+h_{2}+3)+2}{4}=\frac{5n+2}{4}.\]
Subcase 2.2. \(\deg(a_{0})=3\).
By the choice of \(a_{0}\), any vertex on \(C\) of degree three is either a support vertex or it is adjacent to a support vertex of degree two. Let \(x\) be a vertex of \(C\) adjacent to a support vertex \(w\notin C.\) Let \(v\) denote the leaf neighbor of \(w.\) Remove vertices \(x,w,v\) from \(G\) and let \(T\) be the resulting tree. Since \(n\geq8\), \(|V(T)|\geq3\) and by Theorem 1.1, \(\gamma_{oidR}(T)\leq\frac{5(n-3)}{4}\). In this case, any \(\gamma_{oidR}% (T)\)-function can be extended to an OIDRDF on \(G\) by assigning 2 to \(x,v\) and 0 to \(w\), and therefore, \[\gamma_{oidR}(G)\leq\gamma_{oidR}(T)+4\leq\frac{5(n-3)}{4}+4\leq{\frac {5n+1}{4}<\frac{5n+2}{4}.}\]
Hence, \(G\) has no support vertex outside \(C.\) If each vertex of \(C\) is a support vertex, then by Proposition 2.1 we have \(\gamma_{oidR}% (G)\leq\frac{5n+2}{4},\) with equality if and only if \(G=cor(C_{t})\) for some odd \(t\), and so \(G\in\mathcal{U}\). Hence we can assume that at least one vertex of \(C\) has degree two. In this case, let \(x\) be a support vertex of \(C\) having a neighbor \(y\in C\) of degree two. Let \(y_{1}\) denote the second neighbor of \(y\) on \(C.\) If \(\deg(y_{1})=3\), then consider the tree \(T\) obtained from \(G\) by removing \(x,y,y_{1}\) and the two leaf neighbors of \(x\) and \(y_{1}\). Since \(n\geq8\), we have \(|V(T)|\geq3\) and by Theorem 1.1, \(\gamma_{oidR}(T)\leq\frac{5(n-5)}{4}\). In this case, we extend any \(\gamma_{oidR}(T)\)-function to an OIDRDF on \(G\) by assigning 3 to \(x,y_{1}\) and 0 to any other vertex. It follows that; \[\gamma_{oidR}(G)\leq\gamma_{oidR}(T)+6\leq\frac{5(n-5)}{4}+6={\frac{5n-1} {4}<\frac{5n+2}{4}.}%\]
Hence we can assume that \(\deg(y_{1})=2\) and let \(y_{2}\) denote the second neighbor of \(y_{1}\) on \(C\). If \(\deg(y_{2})=3\), then consider the tree \(T\) obtained from \(G\) by removing vertices \(x,y,y_{1},y_{2}\) and the two leaf neighbors of \(x\) and \(y_{2}\). Since \(n\geq8,\) it follows that \(|V(T)|\geq2\). Now, if \(|V(T)|=2\), then \(G\) is one of the two graphs \(U_{1}\) or \(U_{2}\) of Figure 2, but for both graphs we have \(\gamma_{oidR}(G)<\frac {5n+2}{4}\). Hence, we assume that \(|V(T)|\geq3\) and thus by Theorem 1.1, \(\gamma_{oidR}(T)\leq\frac{5(n-6)}{4}\). As before, we can extend any \(\gamma_{oidR}(T)\)-function to an OIDRDF on \(G\) by assigning 3 to \(x,y_{2}\), 1 to \(y\) and 0 to any other vertex. It follows that; \[\gamma_{oidR}(G)\leq\gamma_{oidR}(T)+7\leq\frac{5(n-6)}{4}+7=\frac{5n-2} {4}<\frac{5n+2}{4}.\]
Finally assume that \(\deg(y_{2})=2\), and let \(T\) be the tree obtained from \(G\) by removing vertices \(x,y,y_{1},y_{2}\) and leaf neighbor of \(x\). Since \(n\geq8\), we have \(|V(T)|\geq3\) and thus by Theorem 1.1, \(\gamma _{oidR}(T)\leq\frac{5(n-5)}{4}\). Clearly, any \(\gamma_{oidR}(T)\)-function can be extended to an OIDRDF on \(G\) by assigning 3 to \(x\), 2 to \(y_{2}\), 1 to \(y_{1}\) and 0 to any other vertex. It is easy to see that \(\gamma _{oidR}(G)\leq\gamma_{oidR}(T)+6\leq\frac{5n}{4}.\) This completes the proof. ◻
In this section, we present an upper bound on the OIDR-domination number of connected bicyclic graphs, and we characterize all extremal bicyclic graphs attaining this bound.
Let \(\mathcal{B}\) be the family of bicyclic graphs \(G\) that can be obtained from two graphs \(G_{1},G_{2}\in\mathcal{U}\) by adding an edge between their support vertices so that the resulting graph is bicyclic (for eaxmple see Figure 5).
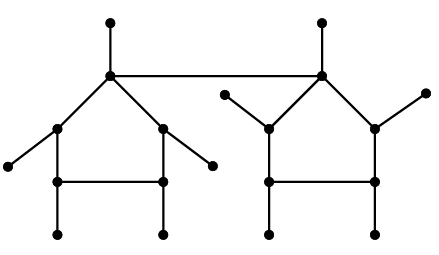
Lemma 3.1. If \(G\in\mathcal{B}\), then \(\gamma_{oidR}(G)=\frac{5n+4}{4}\). Moreover,
(i) for any leaf \(u\) of \(G\) with support vertex \(v\), there exists a \(\gamma_{oidR}(G)\)-function that assigns 2 to \(u\) and \(v\) is doubly Roman dominated by vertices in \(G-u\).
(ii) for any support vertex \(v\) of \(G\), there exists a \(\gamma_{oidR}(G)\)-function that assigns at least 2 to \(v\).
Theorem 3.2. If \(G\) is a connected bicyclic graph of order \(n\), then \[\gamma_{oidR}(G)\leq\frac{5n+4}{4},\] with equality if and only if \(G\in\mathcal{B}\).
Proof. The proof is by induction on \(n\). Clearly, \(n\geq5,\) and one can easily check that the statement holds for all bicyclic graphs of order \(n\in\{5,6,7\}\), establishing the base case. Let \(n\geq8,\) and assume that the result holds for all bicyclic graphs of order less than \(n\). Let \(G\) be a bicyclic graph of order \(n\). Let \(C\) and \(C^{\prime}\) denote the cycles of \(G\), where \(V(C)=\{v_{1},\ldots,v_{\ell}\}\) and \(V(C^{\prime})=\{w_{1}% ,\ldots,w_{m}\}\). Without loss of generality, assume that \(d(C,C^{\prime })=d(v_{1},w_{1})\), and let \(P\) denote the shortest path between \(v_{1}\) and \(w_{1}\). Before going further, we need to state some claims. The first one can be proven similarly to Claim 2, and thus the proof is omitted.
Claim 2. If \(v\in V(P)\cup V(C)\cup V(C^{\prime})\) is a strong support vertex such that all of its neighbors outside \(P\cup C\cup C^{\prime}\) are leaves, or \(v\in V(G)-V(P)\cup V(C)\cup V(C^{\prime})\) is a strong support vertex such that all of its neighbors but one are leaves, then \(\gamma _{oidR}(G)<\frac{5n+4}{4}\).
Claim 3. If \(a_{0}\in V(P)\cup V(C)\cup V(C^{\prime})\) and there is a path of length \(k\geq3\) from \(a_{0}\) to a farthest leaf \(a_{k}\) from \(a_{0}\) that intersects \(P\cup C\cup C^{\prime}\) only in \(a_{0}\), then \(\gamma _{oidR}(G)\leq\frac{5n+4}{4},\) with equality only if \(G\in\mathcal{B}\).
Proof of Claim 3. Suppose that there is a path \(a_{0}% a_{1}\cdots a_{k}\) to a leaf \(a_{k}\) such that \(k\geq3\) and no \(a_{i}\) for any \(i\geq1,\) belongs to \(V(P),V(C)\) or \(V(C^{\prime})\). By Claim 2, \(\deg(a_{k-1})=2\). First, assume that \(\deg(a_{k-2})\geq3\). Suppose that \(a_{k-2}\) has \(q_{1}\) neighbors as support vertices of degree two and \(q_{2}\) neighbors as leaves. Clearly \(q_{1}\geq1\) (because of \(a_{k-1}\)) and \(q_{1}+q_{2}\geq2\) (because of \(\deg(a_{k-2})\geq3\)). Remove \(a_{k-2}\) from \(G\) and consider the component \(G^{\prime}\) that contains \(a_{k-3}.\) Note that \(G^{\prime}\) is bicyclic. If \(q_{2}\geq1\), then any \(\gamma_{oidR}(G^{\prime })\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(a_{k-2}\) and 0 to its neighbors but \(a_{k-3}\), 2 to any other vertex. By the induction hypothesis on \(G^{\prime}\) and since \(q_{1}\geq1\) and \(q_{2}\geq1\), we obtain that; \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2q_{1}% +3\nonumber\label{eqb1}\\ & \leq\frac{5(n-2q_{1}-q_{2}-1)+4}{4}+2q_{1}+3\nonumber\\ & \leq\frac{5n-2q_{1}-5q_{2}+7+4}{4}\leq\frac{5n+4}{4}. \end{aligned} \tag{3}\]
Further if \(\gamma_{oidR}(G)=\frac{5n+4}{4},\) we have equality throughout the inequality chain (3). In particular \(q_{1}=q_{2}=1\) and \(\gamma_{oidR}(G^{\prime})=\frac{5(n-4)+4}{4}\). It follows from the induction hypothesis that \(G^{\prime}\in\mathcal{B}\). If \(a_{k-3}\) is a leaf in \(G^{\prime}\), then by Lemma 3.1, \(G^{\prime}\) has a \(\gamma _{oidR}(G^{\prime})\) that assigns 2 to \(a_{k-3}\) and \(a_{k-4}\) is doubly Roman dominated by the vertices in \(G^{\prime}-a_{k-3}\). In this case, reassigning \(a_{k-3}\) the value 1 and assigning 3 to \(a_{k-2}\), 2 to \(a_{k}\) and 0 to \(a_{k-1}\) and the leaf neighbor of \(a_{k-2}\), provides an OIDRDF of \(G\) of weight \(\gamma_{oidR}(G^{\prime})+4\) which leads to a contradiction. Thus \(a_{k-3}\) is a support vertex of \(G^{\prime}\) and thus \(G\in\mathcal{B}\).
Hence we can assume that \(q_{2}=0\). Then \(q_{1}\geq2\) and any \(\gamma _{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 0 to neighbors of \(a_{k-2}\) but \(a_{k-3}\), 2 to any other remaining vertex. By the induction hypothesis on \(G^{\prime},\) and since \(q_{1}\geq2\), we obtain that; \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2q_{1}+2\\ & \leq\frac{5(n-2q_{1}-1)+4}{4}+2q_{1}+2\\ & \leq\frac{5n-2q_{1}+3+4}{4}<\frac{5n+4}{4}. \end{aligned}\]
In the sequel, we will assume that \(\deg(a_{k-2})=2\). Note that any neighbor of \(a_{k-3},\) except \(a_{k-4}\) when \(k\ge4\) or its neighbors in \(V(P)\cup V(C)\cup V(C^{\prime})\) when \(k=3\), is either a leaf, a support vertex of degree two (because of Claim 2), or a vertex of degree two which is adjacent to a support vertex of degree two. Accordingly, assume that \(a_{k-3}\) is adjacent to \(h_{1}\) leaves, \(h_{2}\) support vertices of degree two and \(h_{3}\) vertices of degree two each of which is adjacent to a support vertex of degree two (all outside C). Because of \(a_{k-2}\), we have \(h_{3}\geq1\).
Assume that \(k\geq4\), and let \(G^{\prime}\) be the component of \(G\) containing \(a_{k-4}\) after the removal of the edge \(a_{k-3}a_{k-4}.\) Observe that \(G^{\prime}\) remains bicyclic. Now, if \(h_{1}\geq1\), then every \(\gamma _{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(a_{k-3}\) and to each support vertex (note in \(G^{\prime}\)) at distance 2 from \(a_{k-3}\), 2 to any leaf (note in \(G^{\prime}\)) at distance two from \(a_{k-3}\) and 0 to any other vertex in \(V(G)-V(G^{\prime})\). By the induction hypothesis on \(G^{\prime}\) and since \(h_{1}\geq1\) and \(h_{3}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3}+3\\ & \leq\frac{5(n-h_{1}-2h_{2}-3h_{3}-1)+4}{4}+2h_{2}+3h_{3}+3\\ & \leq\frac{5n-5h_{1}-2h_{2}-3h_{3}+7+4}{4}<\frac{5n+4}{4}. \end{aligned}\]
Hence let \(h_{1}=0\). Then any \(\gamma_{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to each support vertex (note in \(G^{\prime}\)) at distance 2 from \(a_{k-3}\), 2 to \(a_{k-3}\) and any leaf (note in \(G^{\prime}\)) at distance two from \(a_{k-3}\) and 0 to any other vertex in \(V(G)-V(G^{\prime})\). By the induction hypothesis on \(G^{\prime}\) and since \(h_{3}\geq1\), we obtain
\[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3}% +2\notag\\ & \leq\frac{5(n-2h_{2}-3h_{3}-1)+4}{4}+2h_{2}+3h_{3}+2\nonumber\\ & \leq\frac{5n-2h_{2}-3h_{3}+3+4}{4}\notag\\ &\leq\frac{5n+4}{4}.\label{qqq} \end{aligned} \tag{4}\]
Further if \(\gamma_{oidR}(G)=\frac{5n+4}{4},\) then we have equality throughout the inequality chain (4). In particular, \(h_{2}=0\) and \(h_{3}=1\) and \(\gamma_{oidR}(G^{\prime})=\frac{5(n-4)+4}{4}.\) By the the induction hypothesis, \(G^{\prime}\in\mathcal{B}\), where \(a_{k-4}\) can be a leaf or a support vertex. But in any case, by items (i) and (ii) of Lemma 3.1, \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime})\)-function \(f^{\prime}\) that assigns at least 2 to \(a_{k-4}\). In this case, assigning 2 to \(a_{k},a_{k-2}\), and 0 to \(a_{k-1},a_{k-3}\), \(f^{\prime}\) can be extended to an OIDRDF of \(G\) of weight \(\gamma_{oidR}(G^{\prime})+4<\) \(\frac{5n+2}{4},\) leading to a contradiction. Therefore, the equality does not holds, that is \(\gamma_{oidR}(G)<\frac{5n+2}{4}.\)
In the following, we can assume that \(k=3\). Denote by \(A\) the set of all neighbors of \(a_{0}\) outside of \(C\cup C^{\prime}\cup P,\) and recall that \(h_{3}\geq1\). Let \(G^{\prime}\) be the union of the components of \(G-(A\cup\{a_{0}\})\) containing neighbors of \(a_{0}\) on \(P\cup C_{m}\cup C_{\ell}\).
Consider the following situations.
\(\bullet\) \(a_{0}\in V(P)-\{v_{1},w_{1}\}\).
Since \(a_{0}\in V(P),\) the graph \(G^{\prime}\) is the disjoint union of two unicyclic graphs and thus by Theorem 2.3, \(\gamma_{oidR}(G^{\prime})\leq\frac{5|V(G^{\prime})|+4}{4}\). Now, if \(h_{1}\geq1\), then we extend any \(\gamma_{oidR}(G^{\prime})\)-function to an OIDRDF for \(G\) by assigning 3 to \(a_{0}\) and to each support vertex (not in \(G^{\prime}\)) at distance 2 from \(a_{0}\), 2 to any leaf (not in \(G^{\prime }\)) at distance two from \(a_{0}\) and 0 to any other vertex in \(V(G)-V(G^{\prime})\). Since \(h_{1}\geq1\) and \(h_{3}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3}+3\\ & \leq\frac{5(n-h_{1}-2h_{2}-3h_{3}-1)+4}{4}+2h_{2}+3h_{3}+3\\ & \leq\frac{5n-5h_{1}-2h_{2}-3h_{3}+7+4}{4}\\&<\frac{5n+4}{4}. \end{aligned}\]
Hence we may assume that \(h_{1}=0\). Then any \(\gamma_{oidR}(G^{\prime}% )\)-function can be extended to a OIDRDF of \(G\) by assigning 3 to each support vertex (not in \(G^{\prime}\)) at distance 2 from \(a_{k-3}\), 2 to \(a_{0}\) and to any leaf (not in \(G^{\prime}\)) at distance two from it and 0 to any other vertex in \(V(G)-V(G^{\prime})\). As before, it can be seen that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3} +2\nonumber\label{eqb22}\\ & \leq\frac{5(n-2h_{2}-3h_{3}-1)+4}{4}+2h_{2}+3h_{3}+2\nonumber\\ & \leq\frac{5n-2h_{2}-3h_{3}+3+4}{4}\leq\frac{5n+4}{4}. \end{aligned} \tag{5}\]
Further if \(\gamma_{oidR}(G)=\frac{5n+4}{4},\) then we have equality throughout inequality chain (5). In particular \(h_{3}=1\), \(h_{2}=0\) and \(\gamma_{oidR}(G^{\prime})=\frac{5(n-4)+4}{4}\). It follows that \(G^{\prime}\) is the disjoint union of two unicyclic graphs \(G^{\prime\prime},G^{\prime \prime\prime}\in\mathcal{U}\). By Lemma 2.2, \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime})\)-function such that assigns at least 2 to the neighbors of \(a_{0}\) in \(G^{\prime}\), and such a \(\gamma_{oidR}(G^{\prime}% )\)-function can be extended to an OIDRDF of \(G\) by assigning 2 to \(a_{1}% ,a_{3}\) and 0 to \(a_{0},a_{2}\) which leads to a contradiction. Hence we deduce that \(\gamma_{oidR}(G)<\frac{5n+4}{4}\) which is a contradiction. Therefore, the equality does not holds, that is \(\gamma_{oidR}(G)<\frac{5n+4}{4}.\)
\(\bullet\) \(a_{0}\in V(C)\cup V(C^{\prime})\setminus\{v_{1},w_{1}\}\).
Since \(a_{0}\in V(C)\cup V(C^{\prime}),\) the graph \(G^{\prime}\) is unicyclic and thus by Theorem 2.3, \(\gamma_{oidR}(G^{\prime})\leq\frac{5|V(G^{\prime })|+2}{4}\). Now, if \(h_{1}\geq1\), then we extend any \(\gamma_{oidR}(G^{\prime })\)-function to an OIDRDF for \(G\) by assigning 3 to \(a_{0}\) and to each support vertex (not in \(G^{\prime}\)) at distance 2 from \(a_{0}\), 2 to any leaf (not in \(G^{\prime}\)) at distance two from \(a_{0}\) and 0 to any other vertex in \(V(G)-V(G^{\prime})\). Since \(h_{1}\geq1\) and \(h_{3}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3}+3\\ & \leq\frac{5(n-h_{1}-2h_{2}-3h_{3}-1)+2}{4}+2h_{2}+3h_{3}+3\\ & \leq\frac{5n-5h_{1}-2h_{2}-3h_{3}+5+4}{4}\\&<\frac{5n+4}{4}. \end{aligned}\]
Hence we may assume that \(h_{1}=0\). Then any \(\gamma_{oidR}(G^{\prime}% )\)-function can be extended to a OIDRDF of \(G\) by assigning 3 to each support vertex (not in \(G^{\prime}\)) at distance 2 from \(a_{k-3}\), 2 to \(a_{0}\) and to any leaf (not in \(G^{\prime}\)) at distance two from it and 0 to any other vertex in \(V(G)-V(G^{\prime})\). As before, we have \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{2}+3h_{3}+2\notag\\ & \leq\frac{5(n-2h_{2}-3h_{3}-1)+2}{4}+2h_{2}+3h_{3}+2\nonumber\\ & \leq\frac{5n-2h_{2}-3h_{3}+3+2}{4}\notag\\&\leq\frac{5n+4}{4}.\label{4q} \end{aligned} \tag{6}\]
Further if \(\gamma_{oidR}(G)=\frac{5n+4}{4},\) then we have equality throughout the inequality chain (6). In particular, \(h_{2}=0\) and \(h_{3}=1\) and \(\gamma_{oidR}(G^{\prime})=\frac{5(n-4)+4}{4}.\) By the induction hypothesis, \(G^{\prime}\in\mathcal{U}\), where a neighbor of \(a_{0}\) in \(V(C)\cup V(C^{\prime})\) that belongs to \(G^{\prime}\) is either a leaf or a support vertex. But in either case, by items (i) and (ii) of Lemma 2.2, such a neighbor in \(G^{\prime}\) is assigned at least 2 under some \(\gamma_{oidR}(G^{\prime})\)-function \(f^{\prime}\) that can be extended to an OIDRDF of \(G\) of weight \(\gamma_{oidR}(G^{\prime})+4\) by assigning 1 to \(a_{0},\) 3 to \(a_{2}\) and 0 to both \(a_{3}\) and \(a_{1}.\) Clearly, all this leads to a contradiction. Therefore, the equality does not holds, that is \(\gamma_{oidR}(G)<\frac{5n+4}{4}.\)
\(\bullet\) \(a_{0}\in\{v_{1},w_{1}\}\).
If \(a_{0}=v_{1}=w_{1}\) and \(G^{\prime}=K_{2}\cup K_{2}\), then the function \(f\) defined on \(V(G)\) by assigning 3 to \(a_{0}\) and each support vertex at distance 2 from \(a_{0}\), 2 to any leaf at distance two from \(a_{0}\), 1 to \(v_{2},w_{2}\) and 0 to any other vertex in \(V(G)-V(G^{\prime})\), is an OIDRDF of \(G\) of weight \(3h_{3}+2h_{2}+5\), and clearly \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). Hence, without loss of generality, we assume that \(a_{0}=v_{1}\). If \(G^{\prime}\) has no \(K_{2}\)-component, then using a similar argument as before, we can see that \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). Otherwise, let \(G^{\prime\prime}\) be the component of \(G-a_{0}\) of order at least three and containing no vertex of \(A.\) If \(v_{1}=w_{1},\) then the graph \(G^{\prime\prime}\) is a tree, otherwise \(G^{\prime\prime}\) is a unicyclic graph and thus by Theorems 1.1 and 2.3, \(\gamma_{oidR}(G^{\prime\prime}% )\leq\lfloor\frac{5|V(G^{\prime\prime})|+2}{4}\rfloor\). In this case, we extend any \(\gamma_{oidR}(G^{\prime\prime})\)-function to an OIDRDF of \(G\) by assigning 3 to \(v_{1}\) and to each support vertex (not in \(G^{\prime\prime}\)) at distance 2 from it, 2 to any leaf (not in \(G^{\prime\prime}\)) at distance two from \(v_{1}\), \(1\) to \(v_{2}\) and 0 to any other vertex in \(V(G)-V(G^{\prime\prime})\). Now, we have \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime\prime})+2h_{2}+3h_{3}+4\\ & \leq\frac{5(n-h_{1}-2h_{2}-3h_{3}-3)+2}{4}+2h_{2}+3h_{3}+4\\ & \leq\frac{5n-5h_{1}-2h_{2}-3h_{3}+3}{4}\\&<\frac{5n+4}{4}. \end{aligned}\] ◻
Therefore, in the next we can consider that \(k\leq2,\) that is every leaf in \(G\) (if any) is at distance at most two from some vertex of \(V(P)\cup V(C)\cup V(C^{\prime}).\) We proceed with the following claim.
Claim 4. If \(v\in V(P)\cup V(C)\cup V(C^{\prime})-\{v_{1},w_{1}\}\) and \(\deg(v)\geq4\), then \(\gamma_{oidR}(G)\leq\frac{5n+4}{4}\). Moreover, if the equality holds, then \(G\in\mathcal{B}\).
Proof of Claim 4. Let \(v\in V(P)\cup V(C)\cup V(C^{\prime })-\{v_{1},w_{1}\}\) such that \(\deg(v)\geq4\). By Claims 2 and 3, each neighbor of \(v\) outside \(V(P)\cup V(C)\cup V(C^{\prime})\) is a leaf or a support vertex of degree two. Suppose that the neighbors of \(v\) outside \(V(P)\cup V(C)\cup V(C^{\prime})\) are \(h_{1}\) support vertices of degree two and \(h_{2}\) leaves. Clearly, \(h_{1}+h_{2}\geq2\). Remove \(v\) from \(G\), and consider the following two situations.
\(\bullet\) \(v\in V(C)\cup V(C^{\prime})-\{v_{1},w_{1}\}\).
Let \(G^{\prime}\) be the component of \(G-v\) containing \(v_{1}.\) Then \(G^{\prime}\) is a unicyclic graph. Now, if \(h_{2}\geq1\), then any \(\gamma_{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(v\) and 0 to its neighbors outside \(C\cup C^{\prime}\), and 2 to any other vertex. By Theorem 2.3 and since \(h_{1}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{1}+3\\ & \leq\frac{5(n-2h_{1}-h_{2}-1)+2}{4}+2h_{1}+3\\ & \leq\frac{5n-2h_{1}-5h_{2}+5+4}{4}\\&<\frac{5n+4}{4}. \end{aligned}\]
If \(h_{2}=0\), then \(h_{1}\geq2\) and any \(\gamma_{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 0 to neighbors of \(v\) outside \(C\cup C^{\prime},\) and 2 to any other vertex (including \(v\)). By Theorem 2.3 and since \(h_{1}\geq2\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+2h_{1}+2\\ & \leq\frac{5(n-2h_{1}-1)+2}{4}+2h_{1}+2\\ & \leq\frac{5n-2h_{1}+1+4}{3}\\&<\frac{5n+4}{4}.\\ \end{aligned}\]
\(\bullet\) \(v\in V(P)\).
Let \(G^{\prime}\) be the component of \(G-v\) containing \(v_{1}\) and \(G^{\prime\prime}\) be the component of \(G-v\) containing \(w_{1}\). Then \(G^{\prime}\) and \(G^{\prime\prime}\) are unicyclic graphs. Now, if \(h_{2}\geq1\), then any \(\gamma_{oidR}(G^{\prime}\cup G^{\prime\prime}% )\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(v\) and 0 to its neighbors outside \(C\cup C^{\prime}\), and 2 to any other vertex. By Theorem 2.3 and since \(h_{1}\geq1\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+\gamma_{oidR} (G^{\prime\prime})+2h_{1}+3\\ & \leq\ \frac{{5(n-2h_{1}-h_{2}-1)+4}}{4}+2h_{1}+3\\ & \leq\frac{5n-2h_{1}-5h_{2}+7+4}{4}\\&\leq\frac{5n+4}{4}. \end{aligned}\]
Further if \(\gamma_{oidR}(G)=\frac{5n+4}{4}\), then we have equality throughout the previous inequality chain. In particular \(h_{1}=h_{2}=1,\) \(\gamma _{oidR}(G^{\prime})=\frac{5n(G^{\prime})+2}{4}\) and \(\gamma_{oidR}% (G^{\prime\prime})=\frac{5n(G^{\prime\prime})+2}{4}\). Theorem 2.3 implies that \(G^{\prime},G^{\prime\prime}\in\mathcal{U}\). Let \(u\) be a vertex of \(G^{\prime}\) which is the neighbor of \(v\) on the path \(P.\) If \(u\) is a leaf, then by Lemma 2.2, \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime}% )\)-function \(f^{\prime}\) such that assigns weight 2 to \(u\) and the support vertex of \(u\) in \(G^{\prime}\) is doubly Roman dominated by vertices in \(G^{\prime}-u\). In this case, if \(f^{\prime\prime}\) is a \(\gamma _{oidR}(G^{\prime\prime})\)-function, then reassigning \(u\) the value 1, and assigning 3 to \(v\), 2 to the leaf at distance 2 from \(v\) not in \(V(G^{\prime })\cup V(G^{\prime\prime})\) and 0 to the neighbors of \(v\) not in \(V(G^{\prime })\cup V(G^{\prime\prime})\), provides an OIDRDF of \(G\) with weight \(\gamma_{oidR}(G^{\prime})+\gamma_{oidR}(G^{\prime\prime})+4\), leading to a contradiction. Thus the neighbors of \(v\) in \(G^{\prime}\) and \(G^{\prime}\) are support vertices and one can see easily that \(G\in\mathcal{B}\).
If \(h_{2}=0\), then \(h_{1}\geq2\) and any \(\gamma_{oidR}(G^{\prime}\cup G^{\prime\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 0 to neighbors of \(v\) outside \(G^{\prime}\cup G^{\prime\prime},\) and 2 to any other vertex (including \(v\)). By Theorem 2.3 and since \(h_{1}\geq2\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+\gamma_{oidR} (G^{\prime\prime})+2h_{1}+2\\ & \leq\frac{5(n-2h_{1}-1)+4}{4}+2h_{1}+2\\ & \leq\frac{5n-2h_{1}+3+4}{3}<\frac{5n+4}{4}. \end{aligned}\] ◻
According to Claim 4, if \(v\in V(P)\cup V(C)\cup V(C^{\prime}% )-\{v_{1},w_{1}\}\), then \(\deg(v)\in\{2,3\}\). In particular, if \(\deg(v)=3,\) then \(v\) is either a support vertex or adjacent to a support vertex (outside \(V(P)\cup V(C)\cup V(C^{\prime})\)) of degree two. Likewise, if \(v_{1}\neq w_{1}\), then we may assume that \(3\leq\deg(v_{1})\leq4\) and \(3\leq\deg (w_{1})\leq4\), and if \(v_{1}=w_{1}\), then we may assume that \(4\leq\deg (v_{1})\leq5\). In particular, if \(\deg(v_{1})=5\) with \(v_{1}=w_{1}\) or \(\deg(v)=4\) with \(v\in\{v_{1},w_{1}\}\) and \(v_{1}\neq w_{1}\), then \(v\) is either a support vertex or adjacent to a support vertex (outside \(V(P)\cup V(C)\cup V(C^{\prime})\)) of degree two or \(v_{1}=w_{1}\). We continue with following claims.
Claim 5. Let \(x\in V(P)\cup V(C)\cup V(C^{\prime})-\{v_{1},w_{1}\}\) such that \(\deg(x)=3\) and \(x\) is adjacent to a support vertex outside of \(V(P)\cup V(C)\cup V(C^{\prime})\), then \(\gamma_{oidR}(G)<\frac{5n+4}{4}\).
Proof of Claim 5. Let \(xx_{1}x_{2}\) be a path from \(x\) to a leaf \(x_{2},\) with \(x_{1},x_{2}\notin V(P)\cup V(C)\cup V(C^{\prime})\). First assume that \(x\in V(C)\cup V(C^{\prime})\), and consider the graph \(G^{\prime}\) obtained from \(G\) by removing vertices \(x,x_{1}\) and \(x_{2}.\) Observe that \(G^{\prime}\) is a unicyclic graph, and thus by Theorem 2.3, \(\gamma_{oidR}(G^{\prime})\leq\frac{5(n-3)+2}{4}\). Moreover, since \(\gamma_{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 2 to \(x,x_{2}\) and 0 to \(x_{1}\), we obtain that \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+4\\ & \leq\frac{5(n-3)+2}{4}+4\\ & =\frac{5n+3}{4}\\&<\frac{5n+4}{4}. \end{aligned}\]
Now assume that \(x\in V(P)\), and let \(G^{\prime}\) be obtained from \(G\) by removing vertices \(x,x_{1},x_{2}\). Clearly \(G^{\prime}\) is a disjoint union of two unicyclic graphs \(G_{1}\) and \(G_{2}\). If \(G_{1},G_{2}\notin\mathcal{U}\), then \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime})\)-function \(f\) such that \(\omega(f)\leq\frac{5n(G^{\prime})+2}{4}\), and thus \(f\) can be extended to an OIDRDF of \(G\) by assigning 2 to \(x,x_{2}\) and 0 to \(x_{1}\), yielding as above \(\gamma_{oidR}(G)<\frac{5n+4}{4}.\) If \(G_{1},G_{2}\in\mathcal{U}\), then \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime})\)-function \(f\) such that \(f\) assigns at least two to the neighbors of \(x\) in \(G^{\prime}\), and thus \(f\) can be extended to an OIDRDF of \(G\) by assigning 2 to \(x_{2}\), 1 to \(x_{1}\) and 0 to \(x\), leading again \(\gamma_{oidR}(G)<\frac{5n+4}{4}.\) Hence, we assume that \(G_{1}\in\mathcal{U}\) and \(G_{2}\notin\mathcal{U}\). Then clearly the graph \(G_{3}\) induced by \(V(G)-V(G_{1})\) is a unicyclic graph not belonging to \(\mathcal{U}\). Let \(f_{1}\) be a \(\gamma_{oidR}(G_{1})\)-function such that assigns at least 2 to the neighbor of \(x\) in \(G_{1}\) and let \(f_{3}\) be a \(\gamma_{oidR}(G_{3})\)-function. Obviously combining the function \(f_{1}\) and \(f_{3}\) provides an OIDRDF of \(G\) with weight \(\frac{5n+3}{4}<\frac{5n+4}{4}.\) ◻
Claim 6. If \(v_{1}=w_{1}\) and \(v_{1}\) is adjacent to a support vertex outside of \(V(P)\cup V(C)\cup V(C^{\prime})\), then \(\gamma_{oidR}% (G)<\frac{5n+4}{4}\).
Proof of Claim 6. Suppose that \(v_{1}x_{1}x_{2}\) is a path from \(v_{1}\) to a leaf \(x_{2},\) with \(x_{1},x_{2}\notin V(P)\cup V(C)\cup V(C^{\prime})\). Let \(G^{\prime}\) and \(G^{\prime\prime}\) be the components of \(G-\{v_{1},x_{1},x_{2}\}\) containing \(v_{2}\) and \(w_{2}\) respectively. If \(G^{\prime}\cong G^{\prime\prime}\cong K_{2}\), then assigning 3 to \(v_{1}\), 2 to \(x_{2}\), 1 to \(v_{2},w_{2}\) and 0 to \(v_{3},w_{3}\) provides an OIDRDF of \(G\) and so \(\gamma_{oidR}(G)\leq7<\frac{5n+4}{4}\). Hence we may assume that \(n(G^{\prime\prime})\geq3\). Clearly \(G^{\prime\prime}\) is a tree of order at least 3. If \(G^{\prime}\cong K_{2}\), then any \(\gamma_{oidR}(G^{\prime\prime })\)-function can be extended to an OIDRDF of \(G\) by assigning 2 to \(v_{1},x_{2}\), 1 to \(v_{2},v_{3}\) and 0 to \(x_{1}\). Using Theorem 2.3 on \(G^{\prime\prime}\) we obtain \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime\prime})+6\\ & \leq\frac{5(n-5)}{4}+6\\ & <\frac{5n+4}{4}. \end{aligned}\]
Finally, assume that \(n(G^{\prime})\geq3\). Clearly \(G^{\prime}\) and \(G^{\prime\prime}\) are trees, each of order at least 3. Let \(f_{1}\) be a \(\gamma_{oidR}(G^{\prime})\)-function and \(f_{2}\) be a \(\gamma_{oidR}% (G^{\prime\prime})\)-function. Considering the functions \(f_{1}\) and \(f_{2}\) and assigning 2 to \(v_{1},x_{2}\) and 0 to \(x_{1}\) provides an OIDRDF of \(G\) of weight at most \(\frac{5n+1}{4}<\frac{5n+4}{4}\). ◻
Claim 7. If \(v_{1}=w_{1}\) and \(v_{1}\) is a support vertex, then \(\gamma_{oidR}(G)<\frac{5n+4}{4}\).
Proof of Claim 7. Let \(x\) be the leaf neighbor of \(v_{1}\), and let \(G^{\prime}\) and \(G^{\prime\prime}\) be the components of \(G-\{v_{1},x\}\) containing \(v_{2}\) and \(w_{2}\) respectively. If \(G^{\prime }\cong G^{\prime\prime}\cong K_{2}\), then assigning 3 to \(v_{1}\), 1 to \(v_{2},w_{2}\) and 0 to \(v_{3},w_{3},x\) provides an OIDRDF of \(G\) and so \(\gamma_{oidR}(G)\leq5<\frac{5n+4}{4}\). Hence we may assume that \(n(G^{\prime\prime})\geq3\). Clearly \(G^{\prime\prime}\) is a tree of order at least 3. If \(G^{\prime}\cong K_{2}\), then any \(\gamma_{oidR}(G^{\prime\prime })\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(v_{1}\), 1 to \(v_{2}\) and 0 to \(x,v_{3}\). Using Theorem 2.3 on \(G^{\prime\prime}\) we obtain \[\begin{aligned} \gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime\prime})+4\\ & \leq\frac{5(n-4)}{4}+4\\ & <\frac{5n+4}{4}. \end{aligned}\]
Finally, assume that \(n(G^{\prime})\geq3\) and \(n(G^{\prime\prime})\geq3\). Clearly \(G^{\prime}\) and \(G^{\prime\prime}\) are trees, each of order at least 3. Let \(f_{1}\) be a \(\gamma_{oidR}(G^{\prime})\)-function and \(f_{2}\) be a \(\gamma_{oidR}(G^{\prime\prime})\)-function. Considering the functions \(f_{1}\) and \(f_{2}\) and assigning 3 to \(v_{1}\) and 0 to \(x\) provides an OIDRDF of \(G\) of weight at most \(\frac{5n+2}{4}<\frac{5n+4}{4}\). ◻
Claim 8. If \(v_{1}=w_{1}\) and \(\deg(v_{1})=4\), then \(\gamma _{oidR}(G)<\frac{5n+4}{4}\).
Proof of Claim 8. If \(G-v_{1}=K_{2}\cup K_{2}\), then the function \(f\) defined on \(V(G)\) by assigning 3 to \(v_{1}\), 1 to \(v_{2},w_{2}\) and 0 to \(v_{3},w_{3}\), is an OIDRDF of \(G\) of weight \(5\), and clearly \(\gamma_{oidR}(G)\leq5<\frac{5n+4}{4}\). If \(G^{\prime}=G-v_{1}\) has no \(K_{2}%\)-component, then \(G^{\prime}\) is a forest with two components each of which is a tree of order at least 3. Clearly any \(\gamma_{oidR}(G^{\prime}% )\)-function can be extended to an OIDRDF of \(G\) by assigning 2 to \(v_{1}\) and using Corollary 1.2, we can see that \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). Finally, assume, without loss of generality, that \(G^{\prime\prime}\) is the component of \(G-v_{1}\) of order at least three containing \(w_{2}\). Then \(G^{\prime\prime}\) is a tree and any \(\gamma_{oidR}(G^{\prime\prime}% )\)-function can be extended to an OIDRDF of \(G\) by assigning a 2 to \(v_{1},v_{2}\) and \(0\) to \(v_{3}\). Using Corollary 1.2, we can see that \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). ◻
Claim 9. Let \(x\in\{v_{1},w_{1}\}\) such that \(\deg(x)=4\) and \(x\) is adjacent to a support vertex outside of \(V(P)\cup V(C)\cup V(C^{\prime})\). Then \(\gamma_{oidR}(G)<\frac{5n+4}{4}\).
Proof of Claim 9. Clearly \(v_{1}\neq w_{1}\). Suppose, without loss of generality, that \(x=v_{1}\) and let \(xx_{1}x_{2}\) be a path from \(x\) to a leaf \(x_{2},\) with \(x_{1},x_{2}\notin V(P)\cup V(C)\cup V(C^{\prime})\). Let \(G^{\prime}\) and \(G^{\prime\prime}\) be the components of \(G-\{x,x_{1},x_{2}\}\) containing \(v_{2}\) and \(w_{2},\) respectively, and note that \(G^{\prime\prime}\) is a unicycle graph. By Theorem 2.3, \(\gamma_{oidR}(G^{\prime\prime})\leq\frac{5\left\vert V(G^{\prime\prime })\right\vert +2}{4}.\) Now, if \(G^{\prime}\cong K_{2}\), then assigning 3 to \(x\), 2 to \(x_{2}\), 1 to \(v_{2}\) and 0 to \(v_{3},w_{1}\) provides an OIDRDF of \(G\) and so \(\gamma_{oidR}(G)\leq6<\frac{5n+4}{4}\). Hence we may assume that \(n(G^{\prime})\geq3\), thus \(G^{\prime}\) is a tree. Let \(f_{1}\) be a \(\gamma_{oidR}(G^{\prime})\)-function and \(f_{2}\) be a \(\gamma_{oidR}% (G^{\prime\prime})\)-function. Considering the functions \(f_{1}\) and \(f_{2}\) and assigning 2 to \(x,x_{1}\) and 0 to \(x_{1}\) provides an OIDRDF of \(G\) of weight at most \(\frac{5n+3}{4}<\frac{5n+4}{4}\). ◻
According to the previous claims, each vertex outside of \(V(P)\cup V(C)\cup V(C^{\prime})\) is a leaf and \(v_{1}\neq w_{1}\).
Claim 10. If \(x\in\{v_{1},w_{1}\}\) and \(\deg(x)=3\), then \(\gamma _{oidR}(G)<\frac{5n+4}{4}\).
Proof of Claim 10. Suppose, without loss of generality, that \(x=v_{1}\). Clearly, \(v_{1}\neq w_{1},\) and thus let \(y\) be the third neighbor of \(v_{1}.\) Note that \(y\) may be \(w_{1}.\) Now, if each vertex of \(C\) other than \(v_{1}\) is of degree 2, then let \(G^{\prime}\) be the graph obtained from \(G\) by removing the edge \(v_{1}y.\) Let \(G_{1}\) be the component of \(G^{\prime }\) containing \(v_{1}\) and \(G_{2}\) the component of \(G^{\prime}\) containing \(w_{1}\). Then \(G_{1}\) is a cycle and \(G_{2}\) is a unicyclic graph. Clearly \(G_{1}\) has a \(\gamma_{oidR}(G_{1})\)-function \(f_{1}\) that assigns at least 2 to \(v_{1}\). Now combining \(f_{1}\) with any \(\gamma_{oidR}(G_{2})\) provides an OIDRDF of \(G\) and by Proposition 1.4 and Theorem 2.3, we have \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). Hence let \(i\) be the smallest integer that \(\deg(v_{i})=3\) and so \(v_{i}\) has a leaf neighbor \(w\). If \(i\geq3\), then let \(G^{\prime}\) be the graph obtained from \(G\) by removing the vertices \(v_{i},v_{i-1},w\). Note that \(G^{\prime}\) is unicyclic. Also, since any \(\gamma_{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(v_{i}\), 1 to \(v_{i-1}\), and 0 to \(w\), Theorem 2.3 leads to \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). Hence we can assume that \(i=2\). If \(\ell=3\) and \(\deg(v_{\ell})=2\), then let \(G^{\prime}\) be the graph obtained from \(G\) by removing the vertices \(v_{1},v_{2},v_{3},w\). Since any \(\gamma_{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(v_{2}\), 1 to \(v_{1}\), and 0 to \(v_{3},w\), Theorem 2.3 leads to \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). If \(\ell=3\) and \(\deg(v_{\ell}% )=3\), then consider the component \(G_{2}\) containing \(w_{1}\) obtained by removing the edge \(v_{1}y.\) If \(f_{2}\) is a \(\gamma_{oidR}(G_{2})\)-function, then \(f_{2}\) can be extended to an OIDRDF on \(G\) by assigning 3 to \(v_{2},\) \(2\) to the leaf neighbor of \(v_{\ell},\) 1 to \(v_{1}\) and 0 to \(v_{\ell}\) and \(w.\) Applying Theorem 2.3 on \(G_{2},\) we obtain that \(\gamma _{oidR}(G)<\frac{5n+4}{4}.\) Finally, assume that \(\ell\geq4.\) Remove \(v_{2},w\) from \(G\) and let \(G^{\prime}\) be the resulting unicyclic graph. Clearly, because of the degree of \(v_{1}\) in \(G^{\prime},\) \(G^{\prime}\notin \mathcal{U}\), and thus it satisfies \(\gamma_{oidR}(G^{\prime})<\frac {5\left\vert V(G^{\prime})\right\vert +2}{4}.\) Now, since any \(\gamma _{oidR}(G^{\prime})\)-function can be extended to an OIDRDF of \(G\) by assigning 3 to \(v_{2}\) and 0 to \(w\), we obtain \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). ◻
According to Claims 8 and 10 we may assume that \(v_{1}\neq w_{1}\) and \(\deg(v_{1})=\deg(w_{1})=4\), that is \(v_{1}\) and \(w_{1}\) are support vertices.
Claim 11. If \(x\in V(P)\cup V(C)\cup V(C^{\prime})\) and \(\deg(x)=2\), then \(\gamma_{oidR}(G)<\frac{5n+4}{4}\).
Proof of Claim 11. First assume, without loss of generality, that \(x\in V(C)\). If each \(\deg(v_{i})=2\) for each \(i\neq1\), then by a similar argument as in the proof of Claim 10, we can see that \(\gamma _{oidR}(G)<\frac{5n+4}{4}\). Hence, let \(i\) be the smallest integer that \(\deg(v_{i})=3\) and \(v_{i}\neq v_{1}\). Clearly, \(i\geq2,\) and again by a similar argument to that used in the proof of Claim 10, we can see that \(\gamma_{oidR}(G)<\frac{5n+4}{4}\).
In the following, we can assume that \(x\in V(P)\). Choose \(x\) such that \(d(x,V(G)-V(P))\) is minimum. Without loss of generality, assume that \(d(x,v_{1})=d(x,V(G)-V(P))\). Let \(P=z_{1}\dots z_{r}\) where \(z_{1}v_{1}% ,z_{r}w_{1}\in E(G)\) and let \(x=z_{s}\). Observe that each \(z_{i}\) with \(i<s\) is a support vertex of degree three. Moreover, each vertex of \(C\) and \(C^{\prime}\) is a support vertex of degree 3, except \(v_{1}\) and \(w_{1}\) that are of degree 4. Let \(z_{i}^{\prime}\) be the leaf neighbor of \(z_{i}\) every \(i<s.\)
Assume first that \(s\geq4\). Let \(G_{1}\) be the component of \(G-z_{2}z_{3}\) containing \(z_{2}\) and \(G_{2}\) the component of \(G-z_{2}z_{3}\) containing \(w_{1}\). Then \(G_{2}\not \in \mathcal{U}\), since \(z_{s}\) is a vertex of degree 2 in \(G_{2}.\) Therefore, by Theorem 2.3, \(\gamma_{oidR}(G_{2}% )<\frac{5\left\vert V(G_{1})\right\vert +2}{4}.\) Furthermore, observe that \(G_{1}\) is a graph obtained from \(cor(C)\) by adding the path \(P_{4}% :z_{1}^{\prime}z_{1}z_{2}z_{2}^{\prime}\) and the edge \(v_{1}z_{1}.\) As a result, \(G_{1}\) belongs to \(\mathcal{U}\) if and only if \(C\) is an odd cycle. If \(G_{1}\in\mathcal{U}\), then by Lemma 2.2, \(G_{1}\) has a \(\gamma _{oidR}(G_{1})\)-function \(f\) such that \(f(z_{2})\geq2\), and combining such a function \(f\) with any \(\gamma_{oidR}(G_{2})\)-function produces an OIDRDF of \(G\) leading to \(\gamma_{oidR}(G)<\frac{5n+4}{4}\). If \(G_{1}\notin\mathcal{U}\), then \(\ell\) is certainly even and \(cor(C)\) has a \(\gamma_{oidR}(cor(C))\) -function \(f\) that assigns a 3 to \(v_{1}.\) In this case, \(f\) can be first extended to an OIDRDF \(f_{1}\) on \(G_{1}\) of weight \(\gamma_{oidR}% (cor(C))+5=\frac{5\left\vert V(G_{1})\right\vert }{4}\) by assigning 3 to \(z_{2},\) 2 to \(z_{1}^{\prime}\) and 0 to \(z_{1}\) and \(z_{2}^{\prime}.\) Then combining such a function \(f_{1}\) with any \(\gamma_{oidR}(G_{2})\)-function produces an OIDRDF of \(G\) leading to \(\gamma_{oidR}(G)<\frac{5n+4}{4}\).
Assume that \(s=3\). Let \(G_{1}\) be the component of \(G^{\prime}=G-\{z_{1}% ,z_{2},z_{1}^{\prime},z_{2}^{\prime},z_{3}\}\) containing \(v_{1}\) and \(G_{2}\) be the component of \(G^{\prime}\) containing \(w_{1}\). Note that \(G^{\prime }=cor(C),\) and thus \(G^{\prime}\) has a \(\gamma_{oidR}(G^{\prime})\)-function \(f\) such that \(f(v_{1})\geq2\). Let \(G_{2}\) denote the component containing \(w_{1}.\) By Theorem 2.3, \(\gamma_{oidR}(G_{2})\leq\frac{5\left\vert V(G_{2})\right\vert +2}{4}.\) Now, considering \(f\) and any \(\gamma_{oidR}% (G_{2})\)-function we can extend them to an OIDRDF of \(G\) by assigning 2 to \(z_{1}^{\prime}\), 3 to \(z_{2}\), 1 to \(z_{3}\) and 0 to \(z_{1},z_{2}^{\prime}\) leading to \[\begin{aligned} {\ }\gamma_{oidR}(G) & \leq\gamma_{oidR}(G^{\prime})+\gamma_{oidR} (G_{2})+6\\ & \leq\frac{5(n-5)+4}{4}+6<\frac{5n+4}{4}. \end{aligned}\]
The remaining two situations are considered below.
Case 1. \(s=2\).
By the choice of \(x\) we may assume that \(z_{r}\) is a support vertex. Let \(G^{\prime}\) be the graph obtained from \(G\) by removing the edges \(v_{1}z_{1}\) and \(w_{1}z_{r}\). Let \(G_{1}\) and \(G_{2}\) denote the components of \(G^{\prime}\) containing \(v_{1}\) and \(w_{1}\), respectively, and let \(G_{3}\) be the remaining component. Note that \(G_{3}\) is tree that does not belong to \(\mathcal{T}\), since \(z_{2}\) is neither a leaf nor a support vertex. Hence by Theorem 1.3, \(G_{3}\) has a \(\gamma_{oidR}(G_{3})\)-function of weight less than \(\frac{5\left\vert V(G_{3})\right\vert }{4}.\) Moreover, since each of \(G_{1}\) and \(G_{2}\) is a corona of some cycle, let \(f_{i}\) be a \(\gamma_{oidR}(G_{i})\)-function such that \(f_{i}(v_{i})\geq2\) for \(i=1,2\). Combining the functions \(f_{1}% ,f_{2},f_{3}\) we obtain an OIDRDF of \(G\) with weight at most \(\frac{5n+3}{5}\), as desired.
Case 2. \(s=1\).
Let \(G^{\prime}% =G-\{v_{1}z_{1},w_{1}z_{r}\}\). Let the components of \(G^{\prime}\) containing \(v_{1}\), \(w_{1}\) and \(z_{1}\) be \(G_{1}\), \(G_{2}\) and \(G_{3}\), and let \(f_{i}\) be a \(\gamma_{oidR}(G_{i})\)-function for \(i=1,2,3.\) In particular, \(f_{1}\) and \(f_{2}\) are chosen such that \(f_{1}(v_{1})\geq2\) and \(f_{2}(w_{1})\geq2.\) Now, if \(r=1\), then combining the functions \(f_{1},f_{2}\) and assigning 0 to \(z_{1}\) we obtain an OIDRDF of \(G\) with weight at most \(\frac{5n+3}{5}\). If \(r=2\) and \(\deg(z_{2})=2\), then considering the functions \(f_{1},f_{2}\) and assigning 1 to \(z_{1},z_{2}\) we obtain an OIDRDF of \(G\) with weight at most \(\frac{5n+2}{5}\). If \(r=2\) and \(\deg(z_{2})=3\), then considering the functions \(f_{1},f_{2}\) and assigning 3 to \(z_{2}\) and 0 to \(z_{1}\) and the leaf neighbor of \(z_{2}\), we obtain an OIDRDF of \(G\) with weight at most \(\frac{5n+1}{5}\). Hence we can assume that \(r\geq3\). If \(\deg(z_{2})=3\), then \(z_{2}\) becomes a strong support vertex in \(G_{3}\) and so \(G_{3}% \not \in \mathcal{T}\). Hence \(\omega(f_{3})\leq\frac{5|V(G_{3})|-1}{4}\) (see Theorem 1.3). Then considering the functions \(f_{1},f_{2}\) and \(f_{3}\) we obtain an OIDRDF of \(G\) with weight at most \(\frac{5n+3}{5}\). Thus, assume that \(\deg(z_{2})=2\), and let \(G_{1}^{\prime}\) and \(G_{2}^{\prime}\) denote the components of \(G-\{z_{1},z_{2}\}\) containing \(v_{1}\) and \(w_{1},\) respectively. Clearly \(f_{1}\) can be extended to an OIDRDF \(f^{\prime}\) of \(G_{1}^{\prime}\) by assigning 2 to \(z_{2}\) and 0 to \(z_{1}\). In this case, considering \(f^{\prime}\) together with any \(\gamma_{oidR}(G_{2}^{\prime}% )\)-function provides an OIDRDF of \(G\) and so \(\gamma_{oidR}(G)\leq\frac {5n+2}{4}\). ◻
According to the above claims, we may assume that each vertex on \(V(C)\cup V(C^{\prime})\cup V(P)-\{v_{1},w_{1}\}\) has degree 3 and is a support vertex. Also, each of \(v_{1}\) and \(w_{1}\) has degree 4 and is a support vertex too. Let \(P=z_{1}\dots z_{r},\) with \(z_{1}v_{1},z_{r}w_{1}\in E(G).\) Since each \(z_{i}\) is a support vertex of degree three, let \(z_{i}^{\prime}\) be the leaf neighbor of \(z_{i}.\) To achieve the proof, we first assume that \(r\equiv 1\pmod 2\). If \(r=1\), then let \(G_{1}\) and \(G_{2}\) denote the components of \(G-\{z_{1},z_{1}^{\prime}\}\) containing \(v_{1}\) and \(w_{1},\) respectively. In addition, let \(f_{i}\) be a \(\gamma_{oidR}(G_{i})\)-function such that \(f_{1}(v_{1})\geq2\) and \(f_{2}(w_{1})\geq2.\) Considering \(f_{1},f_{2}\) and assigning 2 to \(z_{1}^{\prime}\) and 0 to \(z_{1}\), we obtain an OIDRDF of \(G\) with weight at most \(\frac{5n+2}{4}\). Hence we can assume that \(r\) is odd and equals at least 3. Delete the edge \(v_{1}z_{1}\) and let \(G_{1}\) be the component of \(G-v_{1}z_{1}\) containing \(v_{1}\) and \(G_{2}\) the other component containing \(z_{1}\). Then \(G_{2}\) is a unicyclic graph, but because of \(r\) odd, \(G_{2}\notin\) \(\mathcal{U}\). Moreover, \(G_{1}\) is a unicyclic graph having a \(\gamma_{oidR}(G_{1})\)-function \(f\) of weight at most \(\frac{5|V(G_{1})|+2}% {4}\) with \(f(v_{1})\geq2\). Considering \(f\) and any \(\gamma_{oidR}(G_{2}% )\)-function together provide an OIDRDF of \(G\) with weight at most \(\frac {5n+3}{4}\). Henceforth assume that \(r\equiv0\pmod 2\). Let \(G_{1}\) and \(G_{2}\) be the components containing vertices \(v_{1}\) and \(w_{1},\) respectively obtained as follows: by removing the edge \(v_{1}z_{1}\) when \(r\geq2\) or by removing the edge \(v_{1}w_{1}\) when \(r=0.\) In either case, \(G_{1}\) is a corona of the cycle \(C,\) and has a \(\gamma_{{oidR}}(G_{1})\)-function \(f_{1}\) such that \(f(v_{1})\geq2\). Now, considering \(f_{1}\) with any \(\gamma_{{oidR}}% (G_{2})\)-function \(f_{2}\) together we obtain an OIDRDF of \(G\) leading to \[\gamma_{oidR}(G)\leq\gamma_{oidR}(G_{1})+\gamma_{oidR}(G_{2})\leq \frac{5|V(G_{1})|+2}{4}+\frac{5|V(G_{2})|+2}{4}=\frac{5n+4}{4}. \label{min}% \tag{7}\]
Further, if \(\gamma_{oidR}(G)=\frac{5n+4}{4},\) then we have equality throughout the inequality chain (7). In particular \(\gamma_{oidR}% (G_{1})=\frac{5n(G_{1})+2}{4}\) and \(\gamma_{oidR}(G_{2})=\frac{5n(G_{2})+2}% {4}\). Theorem 2.3 implies that \(G_{1},G_{2}\in\mathcal{U}\) and since \(G\) is obtained from \(G_{1},G_{2}\) by adding an edge between their support vertices, we have \(G\in\mathcal{B}\). This completes the proof. ◻
According to Theorems 1.1, 2.3 and 3.2, we conclude with the following conjecture.
Conjecture 3.3. If \(G\) is a connected cactus graph of order n and having k cycles, then \(\gamma_{oidR}(G)\leq\frac{5n+2k}{4}\).