Let \(G\) be a finite simple undirected \((p, q)\)-graph, with vertex set \(V(G)\) and edge set \(E(G)\) such that \(p = |V(G)|\) and \(q = |E(G)|\). A super edge-magic total labeling \(f\) of \(G\) is a bijection \(f \colon V(G) \cup E(G) \longrightarrow \{1, 2, \dots, p+q\}\) such that for all edges \(uv \in E(G)\), \(f(u) + f(v) + f(uv) = c(f)\), where \(c(f)\) is called a magic constant, and \(f(V(G)) = \{1, \dots, p\}\). The minimum of all \(c(f)\), where the minimum is taken over all the super edge-magic total labelings \(f\) of \(G\), is defined to be the super edge-magic total strength of the graph \(G\). In this article, we work on certain classes of unicyclic graphs and provide evidence to conjecture that the super edge-magic total strength of a certain family of unicyclic \((p, q)\)-graphs is equal to \(2q + \frac{n+3}{2}\).
Throughout this article, we only consider finite simple undirected graphs. Let \(G\) be a finite simple undirected graph with vertex set \(V(G)\) and edge set \(E(G)\). Let us assume that \(|V(G)|=p\) and \(|E(G)|=q\), then \(G\) is called a \((p,q)\)-graph. For any undefined terms and notations in this article, we follow [1].
A magic valuation of a graph \(G\) was first described by Kotzig and Rosa [2] as a bijection \(f\colon V(G)\cup E(G)\longrightarrow \{1,2,\dots , p+q\}\) such that for all edges \(u v\in E(G)\), the sum \(f(u)+f(v)+f(uv)\) is a constant, called as the magic constant of \(f\). A graph is said to be magic if it has a magic valuation. Ringel and Lladó [3] rediscovered this idea and gave it the name edge-magic. We shall use the phrase edge-magic total, as developed by Wallis [4] to distinguish this usage from that of other forms of labelings that utilize the word magic.
In [2], Kotzig and Rosa have demonstrated that the cycles \(C_{n}\), \(n\geq 3\) and the complete bipartite graphs \(K_{m,n}\) with \(m,n\geq 1\), are edge-magic total graphs. They also established that a complete graph \(K_{n}\) is an edge-magic total graph if and only if \(n=1,2,3,5,\) or \(6\). Further, they proved that the disjoint union of \(n\) copies of \(P_{2}\) has an edge-magic total labeling if and only if \(n\) is odd. The bibliography section includes references to several pieces of pertinent literature, including [3, 5-8].
For studies related to magic constants for edge-magic total labelings of certain families of graphs such as certain cycles and crowns of cycles, see [9-11]. Avadayappan, Vasuki, and Jeyanthi [12] introduced the concept of edge-magic total strength of a graph \(G\) as the smallest magic constant over all edge-magic total labelings of \(G\). Let us denote it by \(em(G)\). Let \(f\) be an edge-magic total labeling of \(G\) with magic constant \(c(f)\). By definition, \[em(G)=\min \big\{c(f)\colon f \textrm{ be an edge-magic total labeling of } G \big\}.\]
In this study, we explore an edge-magic total labeling \(f\) of the \((p,q)\)-graph \(G\), such that \(f(V(G))=\{1,2,\dots ,p\}\). Enomoto, Llado, Nakamigawa, and Ringel [13] have defined this type of labeling as a super edge-magic total labeling. If a graph \(G\) contains a super edge-magic total labeling, then \(G\) is called a super edge-magic total. An important aspect of super edge-magic labelings that captivate researchers is the relationships they share with other well-studied labelings like graceful, harmonious, sequential, cordial labelings, and so on. For an in-depth exploration of these interconnections, references such as [14-16] provide valuable insights.
Enomoto, Llado, Nakamigawa, and Ringel [13] established that a complete graph \(K_{n}\) is super edge-magic total if and only if \(n = 1, 2,\) or \(3\) and also proved that a complete bipartite graph \(K_{m,n}\) is super edge-magic total if and only if \(m = 1\) or \(n = 1\). As demonstrated in [13], cycles \(C_{n}\) are super edge-magic total if and only if \(n\) is odd. Some further results on the super edge-magic total graph can be found in [6, 17-18].
A necessary and sufficient condition for a graph to be a super edge-magic total is stated in the following lemma.
Lemma 1 ([14]*Lemma 1). A \((p,q)\)-graph \(G\) is a super edge-magic total graph if and only if there exists a bijection \(f\colon V(G) \longrightarrow \{1,2,\dots , p\}\), such that the set \(\{f(u)+f(v)\colon u v\in E(G)\}\) is a set of \(q\) consecutive integers. And, \(f\) extends to a super edge-magic total labeling with magic constant \(c(f)=p+q+\min\{f(u)+f(v)\colon u v\in E(G)\}\).
In this case, the vertex labeling \(f\) can be extended to a super edge-magic total labeling of \(G\) by defining \(f(uv) = p + q + \min\big\{f(\tilde{u}) + f(\tilde{v}) \colon \tilde{u}\tilde{v} \in E(G)\big\} – f(u) – f(v)\), for every edge \(uv \in E(G)\).
Acharya and Hedge introduced in [19] the concept of strongly indexable graphs and thanks to Lemma 1, it is very easy to see that the concepts of super edge-magic total graph and strongly indexable graph are equivalent.
For any regular super edge-magic total graph, we have the following result.
Lemma 2 ([14]*Lemma 4). Let \(G\) be an \(r\)-regular \((p, q)\)-graph, where \(r > 0\). Let \(f\) be any super edge-magic total labeling of \(G\). Then \(q\) is odd and \(c(f)=\frac{4p + q + 3}{2}\), for all super edge-magic total labeling \(f\).
By using Lemma 2, we can derive that for an odd cycle \(C_{n}\) and with any super edge-magic total labeling \(f\) of \(C_{n}\), \[\begin{split} c(f) & = 2n+ \min\{f(u)+f(v)\colon u v\in E(C_{n})\} = 2n+ \frac{n+3}{2}\\ & \implies \min\{f(u)+f(v)\colon u v\in E(C_{n})\} = \frac{n+3}{2}. \end{split}\]
The article [20] demonstrates that by considering a super edge-magic total labeling of a super edge-magic total graph, we can add vertices and edges to the given graph such that the new graph constructed is also super edge-magic total.
Theorem 1 ([20]*Theorem 2.4). Let \(G_{p}\) be a connected super edge-magic total \((p,q)\)-graph with \(p\geq 3\). Let \(f\) be a super edge-magic total labeling of \(G_{p}\) and let us consider \(F_{f}(G_{p})=\{f(u)+f(v)\colon u v\in E(G_{p})\}\). Let \(\max (F_{f}(G_{p}))= p+t\), and for some \(a\in V(G_{p})\), \(f(a)=t\). We construct a graph \(\widetilde{G_{p}}\), by taking each copy of \(G_{p}\) and \(m K_{1},\ m\geq 1\) and connecting all the vertices of \(mK_{1}\) to the vertex \(a\in V(G_{p})\). Then, \(\widetilde{G_{p}}\) is also a super edge-magic total graph.
The magic constants for super edge-magic total labelings of crowns of cycles and cycles themselves, in general, have also been studied in many articles, for instance, [21,22]. In [23], the concept of super edge-magic total strength of a graph \(G\) was introduced, where it is defined as the minimum magic constant, the minimum taken over all the super edge-magic total labelings of \(G\). We denote it as \(sm(G)\). So, we have \[sm(G)=\min \big\{c(f)\colon f \textrm{ is a super edge-magic total labeling of } G\big\}.\]
The super edge-magic total strength of an odd cycle \(C_{n}\) was found to be \(\frac{5n+3}{2}\), in [23]. More results regarding the super edge-magic total strength of certain families of graphs are demonstrated in [23,24].
Let \(G\) be a super edge-magic total \((p,q)\)-graph. For any \(v\in V(G)\), the number of edges adjacent to vertex \(v\) is called the degree of \(v\), denoted by \(\mathrm{deg}(v)\). Let \(f\) be a super edge-magic total labeling of \(G\), with magic constant \(c(f)\). As noted in [12], each edge’s magic constants are added together to produce the following result:
\[\label{eq:1} q c(f)=\sum_{v\in V(G)}\mathrm{deg}(v)f(v)+\sum_{e\in E(G)}f(e).\tag{1}\]
Also, since \(\text{Im}(f)= \{1,2,\dots , p+q\}\) and \(f(V(G))= \{1,2, \dots ,p\}\), we can derive that \(p+q+3\leq sm(G)\leq 3p\).
In this paper, we are interested in the family of unicyclic graphs which consists of an odd cycle \(C_{n}\) and \(k_i\) pendant vertices adjacent to each \({i}\in V(C_{n})\).
Let us consider \(G(n;k_{1},\dots ,k_{n})\) to be the unicyclic \((p,q)\)-graph consisting of an odd cycle \(C_n=\{a_1,a_2,\dots ,a_n\}\) and \(k_i\) pendant vertices adjacent to the vertex \(a_i,\ 1\leq i\leq n\). Swaminathan and Jeyanthi [24] established a range for the super edge-magic total strength of this family of unicyclic graphs.
Theorem 2 ([24]*Theorem 4). The unicyclic \((p,q)\)-graph \(G(n;k_{1},\dots ,k_{n})\), where \(n=2s+1\), is a super edge-magic total graph and \[\begin{split} & 2q+2+\frac{1}{q}\bigg(m_2+2m_3+\dots + (n-1)m_n+\frac{n(n-1)}{2}\bigg) \leq s m\big(G(n;k_{1},\dots ,k_{n})\big)\\ & \leq 2(k_1+k_3+\dots +k_{2s+1})+3(k_2+k_4+\dots +k_{2s})+2n+s+2, \end{split}\] where \(m_1\geq m_2\geq\dots\geq m_n\) are integers such that \[\{m_1,m_2,\dots ,m_n\}=\{k_1,k_2,\dots , k_n\}.\]
Corollary 1 ([24]Corollary 4.1). For any unicyclic graph \(G(n;k_{1},\dots ,k_{n})\) such that \(k_{i}=k,\) for any \(1\leq i\leq n\), \[sm(G(n;k,\dots ,k))=2n(k+1)+\frac{n+3}{2}.\]
As stated earlier, in this study we will be investigating the super edge-magic total strength of the family of unicyclic graphs having an odd cycle \(C_{n}\) and \(k_{i}\) pendant vertices adjacent to each \(i \in V (C_{n})\). We will compute certain graphs’ super edge-magic total strength and provide supporting evidence for the following conjecture.
Conjecture 1. Let \(G(n;k_{1},\dots ,k_{n})\) be the super edge-magic total unicyclic \((p,q)\)-graph consisting of an odd cycle \(C_n=\{a_1,a_2,\dots ,a_n\}\) and \(k_i\) number of pendant vertices adjacent to each \(a_i,\ 1\leq i\leq n\). Then, \[s m(G(n;k_{1},\dots ,k_{n})) = 2q + \frac{n+3}{2}.\]
In this article, we particularly examine three specific infinite families of graphs belonging to the family of unicyclic graphs \(G(n;k_{1},\dots ,k_{n})\) and provide substantial evidence in favor of our Conjecture 1. Further, all the graphs under consideration have order and size equal. This makes the main results of the paper fascinating, since it is known that graphs of equal order and size which are super edge-magic total can be used as basis to generate and enumerate several other labelings (see, [15]).
A brief structure of this paper is as follows. Section 2 deals with the family of graphs \(G(n;k_{1},\dots ,k_{n})\) with \(k_{i}=k\), for any \(1\leq i\leq n-1\) and \(k_{n}=k+c\), where \(1\leq c < \frac{2n(k+1)}{n-3}\). We further prove that the super edge-magic total strength of this graph satisfies our main conjecture. In Section 3, we study \(G(n;k,\dots ,k,k-c)\), where \(1\leq c\leq k\) and prove that the super edge-magic total strength of this family of graphs satisfies the conjecture. Section 4 is about the unicyclic graph \(G(n,k_{1},\dots ,k_{n})\) with \(k_{i}=k,\) if \(i\neq r,n-r\) and \(k_{r}=k_{n-r}=k+1\) for any odd number \(r\), \(1\leq r< n\). Further, we prove that this family of graphs also satisfies our main conjecture. All of our conclusions from this study are included in Section 5.
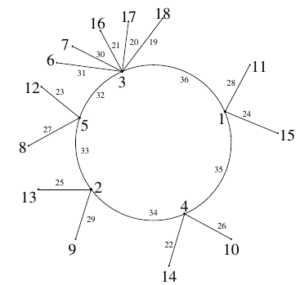
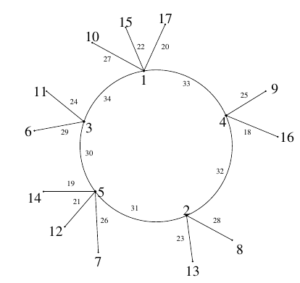
Let \(G_{n,k,c}:= G(n;k,\dots , k,k+c)\), where \(1\leq c < \frac{2n(k+1)}{n-3}\). That is, \(G_{n,k,c}\) is the unicyclic graph consisting of an odd cycle \(C_{n}=\{a_{1},a_{2},\dots , a_{n}\}\), with \(k\) pendant vertices adjacent to each of the vertices \(a_{i},\ 1\leq i\leq n-1\) and \(k+c\) pendant vertices adjacent to vertex \(a_{n}\). For illustration, see Figure 1. Throughout this paper, let \(V(C_{n})= \{a_{1},a_{2},\dots , a_{n}\}\) and \(E(C_{n})= \{a_{i}a_{i+1}\colon 1\leq i \leq n-1\}\cup\{a_{1}a_{n}\}\). The number of vertices and edges of the graph \(G_{n,k,c}\) is \(p=q=n(k+1)+c\). Let the vertex set \(V(G_{n,k,c})\) be \[V(C_{n})\cup \big\{a_{i,j}\colon 1\leq i\leq n-1, 1\leq j\leq k\big\}\cup \big\{a_{n,j}\colon 1\leq j\leq k+c\big\}\] and let the edge set \(E(G_{n,k,c})\) be \[\begin{split} & E(C_{n})\cup\big\{a_{i}a_{i,j}\colon 1\leq i\leq n-1,1\leq j\leq k\big\}\cup\big\{a_{n}a_{n,j}\colon 1\leq j \leq k+c\big\}. \end{split}\]
Theorem 3. The unicyclic graph \(G_{n,k,c}\) is a super edge-magic total graph with super edge-magic total strength given by \[s m(G_{n,k,c})=2n(k+1)+2c+\frac{n+3}{2}.\]
Proof. By Theorem 2, the graph \(G_{n,k,c}:= G(n;k,\dots ,k ,k+c)\), \(1\leq c < \frac{2n(k+1)}{n-3}\), is super edge-magic total. From (1), for any super edge-magic total labeling \(f\) of \(G_{n,k,c}\), we have \[\begin{split} q c(f)&=\sum_{v\in V(G_{n,k,c})}\deg(v)f(v)+\sum_{e\in E(G_{n,k,c})}f(e)\\ & = q(2q+1)+ (k+1)\sum_{a_{i}\in V(C_{n})}f(a_{i})+c f(a_{n}) . \end{split}\]
By assigning the smallest labels to vertices with higher degrees, we get the least possible value of \(c(f)\) as \[\begin{split} & c(f)\geq 2q+1+\frac{(k+1)n(n+1)}{2q}+\frac{c}{q}. \end{split}\]
Hence, we have \[sm(G_{n,k,c})\geq 2q+1+\frac{n(k+1)(n+1)}{2q}+\frac{c}{q}.\]
Since \(sm(G_{n,k,c})\) is an integer, we consider the ceiling of \(\bigg( \frac{n(k+1)(n+1)}{2q}+\frac{c}{q}\bigg)\). We have \(\frac{n+1}{2}-\bigg( \frac{n(k+1)(n+1)}{2q}+\frac{c}{q}\bigg)=\frac{(n-1)c}{2(n(k+1)+c)}\). Since \(1\leq c < \frac{2n(k+1)}{n-3}\), we have \((n-1)c < 2(n(k+1)+c)\). Therefore, \(0< \frac{(n-1)c}{2(n(k+1)+c)} < 1\).
Hence, \[\begin{aligned} s m(G_{n,k,c})&\geq 2q+1+\frac{(n+1)}{2}\\ & = 2n(k+1)+2c+\frac{n+3}{2}. \end{aligned}\] That is, \[\label{eq:lb_k+c} s m(G_{n,k,c})\geq 2n(k+1)+2c+\frac{n+3}{2}.\tag{2}\]
By Theorem 1 and Theorem 2, the graph \(G_{n,k,c}\) can be seen as the super edge-magic total graph constructed from the graph \(G(n;k,\dots , k)\), by connecting all vertices of \(cK_{1}\) to the vertex \(a_{n}\), with the super edge-magic total labeling \(f\) of \(G(n;k,\dots , k)\) defined as follows.
For \(1\leq i \leq n,\) \[\begin{split} &f(a_{i})= \begin{cases} \displaystyle{ \frac{i+1}{2}}& \text{ if } i \text{ is odd}, \\ \\ \displaystyle{\frac{n+i+1}{2}}& \text{ if } i \text{ is even}. \end{cases}\\ & f(a_{i,j})= n(k+1)-(n-1)(j-1)-(i-1),\ 1\leq i\leq n-1,\ 1\leq j\leq k.\\ & f(a_{n,j})= n+j,\ 1\leq j\leq k. \end{split}\]
Now, we extend \(f\) to a vertex labeling \(f\colon V(G_{n,k,c}) \longrightarrow \{1,\dots , p\}\) by defining \[\begin{split} & f(a_{n,j})= n(k+1)+j-k,\ k+1\leq j \leq k+c. \end{split}\]
As per the above labeling, for any \(u v\in E(G_{n,k,c})\) we observe the following.
If \(u, v\in V(G_{n,k,c})\cap V(G(n;k,\dots , k))\), since \(f\) is a super edge-magic total labeling of the graph \(G(n;k,\dots , k)\), the set \(\{f(u)+f(v)\}\) is a consecutive sequence with highest element \(n(k+1)+\frac{n+1}{2}\).
If \(u=a_{n}\) and \(v=a_{n,j}\), for \(k+1\leq j\leq k+c,\) then \(\{f(u)+f(v)\}=\big\{\frac{n+1}{2}+ n(k+1)+1 , \dots , \frac{n+1}{2}+ n(k+1)+ c \big\}\) is a consecutive sequence.
Therefore, we observe that \(\{f(u)+f(v)\colon u v\in E(G_{n,k,c})\}\) is a consecutive sequence and we have \(\min \{f(u)+f(v)\colon u v\in E(G_{n,k,c})\}= \frac{n+3}{2}\). By Lemma 1, the vertex labeling \(f\) extends to a super edge-magic total labeling of \(G_{n,k,c}\) with \(c(f)= 2n(k+1)+2c+\frac{n+3}{2}\). Hence,
\[\label{eq:ub_k+c} s m(G_{n,k,c})\leq 2n(k+1)+2c+\frac{n+3}{2}.\tag{3}\] From (2) and (3), we have \(s m(G_{n,k,c}) = 2n(k+1)+2c+\frac{n+3}{2}.\) ◻
Example 1. Super edge-magic total labeling of the graph \(G_{5,2,3}\) with strength \(s m(G_{5,2,3})= 40\), is illustrated in Figure 1.
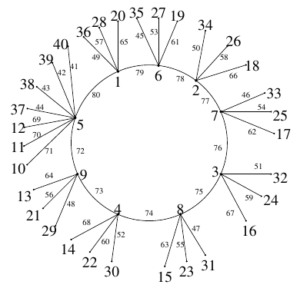
Example 2. Super edge-magic total labeling of \(G_{9,3,4}\) with \(s m(G_{9,3,4})= 86\) is illustrated in Figure 2.
Let us consider the unicyclic graph \(G_{n,k,-c}:= G(n;k,\dots ,k,k-c)\), \(1\leq c\leq k\). For example, see Figure 3. For \(G_{n,k,-c}\), the number of vertices and edges are \(p=q=n(k+1)-c\).
Let \(V(G_{n,k,-c})=V(C_{n})\cup \big\{a_{i,j}\colon 1\leq i\leq n-1, 1\leq j\leq k\big\}\cup \big\{a_{n,j}\colon 1\leq j\leq k-c\big\}\) and let the edge set be equal to \[E(C_{n})\cup\big\{a_{i}a_{i,j}\colon 1\leq i\leq n-1,1\leq j\leq k\big\}\cup\big\{a_{n}a_{n,j}\colon 1\leq j \leq k-c\big\},\] where \(1\leq c\leq k\).
Theorem 4. The unicyclic graph \(G_{n,k,-c}\) is a super edge-magic total graph with super edge-magic total strength \[s m(G_{n,k,-c})=2n(k+1)-2c+\frac{n+3}{2}.\]
Proof. By Theorem 2, the graph \(G_{n,k,-c}\) is super edge-magic total and the lower bound of its super edge-magic total strength is: \[\begin{split} s m(G_{n,k,-c}) & \geq 2q+2+\frac{1}{q}\bigg(\frac{nk(n-1)}{2} +\frac{n(n-1)}{2} -c(n-1) \bigg)\\ & = 2n(k+1)-2c+2+\frac{1}{n(k+1)-c}\bigg(\frac{n(n-1)(k+1)}{2} -c(n-1) \bigg)\\ & = 2n(k+1)-2c+2+\frac{n-1}{2}\bigg(\frac{n(k+1)-2c}{n(k+1)-c}\bigg). \end{split}\]
Since \(s m(G_{n,k,-c})\) is an integer, we consider the ceiling of \(\frac{n-1}{2}\bigg(\frac{n(k+1)-2c}{n(k+1)-c}\bigg)\). We have \(\frac{n-1}{2}-\frac{n-1}{2}\bigg(\frac{n(k+1)-2c}{n(k+1)-c}\bigg)=\frac{(n-1)c}{2(n(k+1)-c)}\). Since \(c\leq k\), we observe that \((n-1)c<2(n(k+1)-c)\). Therefore,
\[\begin{split} & 0< \frac{n-1}{2}-\frac{n-1}{2}\bigg(\frac{n(k+1)-2c}{n(k+1)-c}\bigg) < 1. \end{split}\]
Hence for \(G_{n,k,-c}\), we have \[\begin{aligned} s m(G_{n,k,-c})&\geq 2n(k+1)-2c+2+\frac{n-1}{2}\\ & = 2n(k+1)-2c+\frac{n+3}{2}. \end{aligned}\] That is, \[\label{eq:lb_k-c} s m(G_{n,k,-c})\geq 2n(k+1)-2c+\frac{n+3}{2}.\tag{4}\]
Recall that, our graph \(G_{n,k,-c}\) is the unicyclic graph \(G(n;k,\dots ,k,k-c)\), with \(k\) pendant vertices adjacent to each of the vertices \(a_{i},\ 1\leq i\leq n-1\) and \(k-c\) pendant vertices adjacent to vertex \(a_{n}\), where \(1\leq c \leq k\). Now, we define a vertex labeling \(f\colon V(G_{n,k,-c}) \longrightarrow \{1,\dots , p\}\) as follows:
For \(1\leq i \leq n,\) \[\label{eq:semG} \begin{split} &f(a_{i})= \begin{cases} \displaystyle{ \frac{i+1}{2}}& \text{ if } i \text{ is odd}, \\ \\ \displaystyle{\frac{n+i+1}{2}}& \text{ if } i \text{ is even}. \end{cases}\\ & f(a_{i,j})= n(k+2)-c-(n-1)j-i,\ 1\leq i\leq n-1,\ 1\leq j\leq k.\\ & f(a_{n,j})= n+j,\ 1\leq j\leq k-c. \end{split}\tag{5}\] As per the labeling defined in (5), for any \(u v\in E(G_{n,k,-c})\) we observe the following.
If \(u,v\in V(C_{n})\) then, \(\{f(u)+f(v)\}=\big\{1+\frac{n+1}{2}, \dots , n+\frac{n+1}{2}\big\}\) is a consecutive sequence.
If \(u=a_{n}\) and \(v=a_{n,j}\), \(1\leq j \leq k-c\), then we have \(\{f(u)+f(v)\}=\big\{n+\frac{n+3}{2} , \dots , n+k-c +\frac{n+1}{2} \big\}\), a consecutive sequence.
If \(u=a_{i}\) and \(v=a_{i,j}\), for \(1\leq i\leq n-1,\ 1\leq j\leq k,\) then we have \(\{f(u)+f(v)\}=\big\{n+k-c+\frac{n+3}{2} , \dots , n(k+1)-c+2 \big\}\), which is a consecutive sequence.
Thus we observe that \(\{f(u)+f(v)\colon u v\in E(G_{n,k,-c})\}\) is a consecutive sequence with \(\min \{f(u)+f(v)\colon u v\in E(G_{n,k,-c})\}= \frac{n+3}{2}\). Therefore by Lemma 1, the vertex labeling \(f\) extends to a super edge-magic total labeling of \(G_{n,k,-c}\) with a magic constant \(c(f)= 2n(k+1)-2c+\frac{n+3}{2}\). Hence,
\[\label{eq:ub_k-c} s m(G_{n,k,-c})\leq 2n(k+1)-2c+\frac{n+3}{2}.\tag{6}\] From (4) and (6), we have \(s m(G_{n,k,-c}) = 2n(k+1)-2c+\frac{n+3}{2}\). ◻
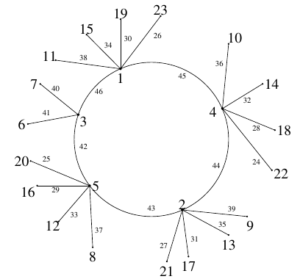
Example 3. Super edge-magic total labeling of the graph \(G_{5,4,-2}\) with super edge-magic total strength \(s m(G_{5,4,-2})= 50\), is illustrated in Figure 3.
Example 4. Super edge-magic total labeling of the graph \(G_{5,8,-6}\) with super edge-magic total strength \(s m(G_{5,8,-6})= 82\), is illustrated in Figure 4.
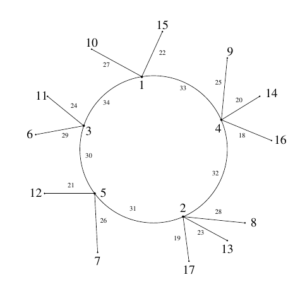
Let \(G(n;k,r)\) be the unicyclic graph \(G(n,k_{1},\dots ,k_{n})\) with \(k_{i}=k,\) if \(i\neq r,n-r\) and \(k_{r}=k_{n-r}=k+1\) for any odd number \(r\), \(1\leq r< n\). See Figure 5. Let \(p=q=n(k+1)+2\), be the number of vertices and edges of \(G(n;k,r)\). Let \[V(G(n;k,r))=V(C_{n})\cup \big\{a_{i,j}\colon 1\leq i\leq n, 1\leq j\leq k\big\}\cup \{a_{r,k+1},a_{n-r,k+1}\},\] and the edge set \(E(G(n;k,r))\) be \[\begin{split} & E(C_{n})\cup\big\{a_{i}a_{i,j}\colon 1\leq i\leq n,1\leq j\leq k\big\}\cup\big\{a_{i}a_{i,k+1}\colon i\in \{r,n-r\}\big\}. \end{split}\]
Theorem 5. The unicyclic graph \(G(n;k,r)\), where \(r\) is any odd number such that \(1\leq r< n\), admits a super edge-magic total labeling and has a super edge-magic total strength \[sm(G(n;k,r))=2n(k+1)+4+\frac{n+3}{2}.\]
Proof. By Theorem 2, the unicyclic graph \(G(n;k,r)\) is a super edge-magic total graph with \[\begin{split} sm(G(n;k,r)) & \geq 2q+2+\frac{1}{q}\bigg((k+1)+2k+\dots + (n-1)k+\frac{n(n-1)}{2}\bigg) \\ & = 2n(k+1)+6+\frac{1}{n(k+1)+2}\bigg(\frac{nk(n-1)}{2} +\frac{n(n-1)}{2} +1\bigg)\\ & = 2n(k+1)+6+\frac{n-1}{2}\bigg(\frac{n(k+1)}{n(k+1)+2}\bigg)+ \frac{1}{n(k+1)+2} . \end{split}\] That is, we have \(sm(G(n;k,r)) \geq 2n(k+1)+6+\frac{n-1}{2}\big(\frac{n(k+1)}{n(k+1)+2}\big)+ \frac{1}{n(k+1)+2}.\) We know that \(s m(G(n;k,r))\) is an integer and we can observe that \[\begin{split} & \frac{n-1}{2} – \bigg (\frac{n-1}{2}\bigg(\frac{n(k+1)}{n(k+1)+2}\bigg) + \frac{1}{n(k+1)+2} \bigg)\\ & = \frac{n-1}{2} \bigg(\frac{2}{n(k+1)+2}\bigg)- \frac{1}{n(k+1)+2} \\ & = \frac{n-2}{n(k+1)+2}\\ & < 1. %\hspace{4cm} \textrm{ (Since, } n-2 < n(k+1)+2) \end{split}\] Hence, we observe that the ceiling of \(\frac{n-1}{2}\big(\frac{n(k+1)}{n(k+1)+2}\big)+ \frac{1}{n(k+1)+2}\) is \(\frac{n-1}{2}\). And we have \[\begin{aligned} sm(G(n;k,r)) & \geq 2n(k+1)+6+\frac{n-1}{2} = 2n(k+1)+4+\frac{n+3}{2}. \end{aligned}\]
Therefore, we can express \[\label{eq:3} sm(G(n;k,r)) \geq 2n(k+1)+4+\frac{n+3}{2}.\tag{7}\]
Now, if we prove that there exists a super edge-magic total labeling \(f\) of \(G(n;k,r)\) with magic constant \(c(f)=2n(k+1)+4+\frac{n+3}{2}\), then our proof is complete.
Let us define a vertex labeling \(f\colon V(G(n;k,r)) \longrightarrow \{1,\dots , p\}\) as follows. For \(1\leq i \leq n,\) \[\label{eq:semlabel1} f(a_{i})= \begin{cases} \displaystyle{ \frac{i+1}{2}}& \text{ if } i \text{ is odd}, \\ \\ \displaystyle{\frac{n+i+1}{2}}& \text{ if } i \text{ is even}. \end{cases}\tag{8}\] And,
\[\label{eq:semlabel2} \begin{split} & f(a_{i,j})= n(k-j+2)-2f(a_{i})+2 ,\ 1\leq i\leq n,\ 1\leq j\leq k-1,\\ & f(a_{i,k})= \begin{cases} 2n +2-2f(a_{i}) & \text{ if } 1\leq f(a_{i})\leq \frac{n+1}{2}, \\ n(k+2) +4 – 2f(a_{i})& \text{ if } \frac{n+3}{2}\leq f(a_{i})\leq n-f(a_{r}), \\ n(k+2) + 2 – 2f(a_{i})& \text{ if } n-f(a_{r})+1 \leq f(a_{i})\leq n, \end{cases}\\ & f(a_{r,k+1})= n(k+1) +2 ,\\ & f(a_{n-r,k+1})= n k+ r +3. \end{split}\tag{9}\]
As per the above labeling, for \(u v\in E(G(n;k,r))\) we observe that:
For \(u,v\in V(C_{n})\), \(\{f(u)+f(v)\}=\big\{1+\frac{n+1}{2}, \dots , n+\frac{n+1}{2}\big\}\) is a consecutive sequence.
Let us consider \(u=a_{i}\) and \(v=a_{i,j}\), for any \(1\leq i\leq n,\ 1\leq j\leq k-1\). Then \(\{f(u)+f(v)\}=\big\{n(k-j+2)-f(a_{i})+2 \colon 1\leq i\leq n,\ 1\leq j\leq k-1\big\}\) is a consecutive sequence with minimal element \(2n+2\) and maximal element \(n (k+1)+1\).
Let \(u=a_{i}\) and \(v=a_{i,k}\), \(1\leq i\leq n\).
If \(1\leq f(a_{i})\leq \frac{n+1}{2},\) then \(\{f(a_{i})+f(a_{i,k})\}= \big\{n+\frac{n+3}{2},\dots , 2n+1\big\}\), is a consecutive sequence.
If \(\frac{n+3}{2}\leq f(a_{i})\leq n-f(a_{r})\), then \(\{f(a_{i})+f(a_{i,k})\}\) is consecutive and equals \(\bigg\{n(k+1)+4+f(a_{r}),\dots , n(k+1)+4+\frac{n-3}{2}\bigg\}.\)
If \(n-f(a_{r})+1 \leq f(a_{i})\leq n,\) then we see that the set \(\{f(a_{i})+f(a_{i,k})\}=\bigg\{n(k+1)+2,\dots , n(k+1)+1+f(a_{r})\bigg\}\), is consecutive.
For \(u=a_{r}\) and \(v=a_{r,k+1}\), \(f(u)+f(v)= n (k+1)+2+f(a_{r})\).
If \(u=a_{n-r}\) and \(v=a_{n-r,k+1}\), then \(f(u)+f(v)= n (k+1)+3 +f(a_{r})\).
Therefore, we observe that \(\{f(u)+f(v)\colon u v\in E(G(n;k,r))\}\) is a consecutive sequence whose minimum element is \(\frac{n+3}{2}\). Hence by Lemma 1, the vertex labeling \(f\) extends to a super edge-magic total labeling of \(G(n;k,r)\) with magic constant \(c(f)= 2n(k+1)+4+\frac{n+3}{2}\). Hence,
\[\label{eq:5} s m(G(n;k,r))\leq 2n(k+1)+4+\frac{n+3}{2}.\tag{10}\]
From (7) and (10), we have \[\begin{split} & 2n(k+1)+4+\frac{n+3}{2} \leq s m(G(n;k,r))\leq 2n(k+1)+4+\frac{n+3}{2}. \end{split}\] This implies, \(s m(G(n;k,r)) = 2n(k+1)+4+\frac{n+3}{2}\). ◻
Example 5. Super edge-magic total labeling of the graph \(G(5;2,1)\) with super edge-magic total strength \(s m(G(5;2,1))= 38\) is illustrated in Figure 5.
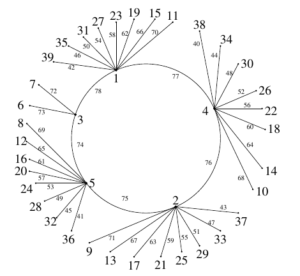
Example 6. Super edge-magic total labeling of the graph \(G(5;2,3)\) with super edge-magic total strength \(s m(G(5;2,3))= 38\) is illustrated in Figure 6.
In this study, we determine the super edge-magic total strength of three variations of \(G(n;k_{1},\dots ,k_{n})\), unicyclic \((p,q)\)-graphs. All three of them have super edge-magic total strength equal to \(2q + \frac{n+3}{2}.\) These results can be considered as the preliminary steps to provide evidence in proving the Conjecture 1.
The author expresses gratitude to Prof. Akihiro Higashitani for his valuable feedback and support, which significantly enhanced the manuscript. The author also expresses thanks to the anonymous reviewers for their attentive reading and insightful suggestions.
The authors declare no conflict of interest
1970-2025 CP (Manitoba, Canada) unless otherwise stated.