The degree of an edge \(uv\) of a graph \(G\) is \(d_G(u)+d_G(v)-2.\) The degree associated edge reconstruction number of a graph \(G\) (or dern(G)) is the minimum number of degree associated edge-deleted subgraphs that uniquely determines \(G.\) Graphs whose vertices all have one of two possible degrees \(d\) and \(d+1\) are called \((d,d+1)\)-bidegreed graphs. It was proved, in a sequence of two papers [1,17], that \(dern(mK_{1,3})=4\) for \(m>1,\) \(dern(mK_{2,3})=dern(rP_3)=3\) for \(m>0, ~r>1\) and \(dern(G)=1\) or \(2\) for all other bidegreed graphs \(G\) except the \((d,d+1)\)-bidegreed graphs in which a vertex of degree \(d+1\) is adjacent to at least two vertices of degree \(d.\) In this paper, we prove that \(dern(G)= 1\) or \(2\) for this exceptional bidegreed graphs \(G.\) Thus, \(dern(G)\leq 4\) for all bidegreed graphs \(G.\)
All graphs considered in this paper are finite, simple and undirected. We shall mostly follow the graph theoretic terminology of [8]. A vertex-deleted subgraph or card \(G-v\) of a graph (digraph) \(G\) is the unlabeled graph (digraph) obtained from \(G\) by deleting the vertex \(v\) and all edges (arcs) incident with \(v\). The deck of a graph (digraph) \(G\) is its collection of cards. A graph (digraph) \(G\) is reconstructible if it can be uniquely determined from its deck. The well-known Reconstruction Conjecture (RC) due to Kelly [10] and Ulam [23] asserts that every graph with at least three vertices is reconstructible. The conjecture has been proved for many special classes, and many properties of \(G\) may be deduced from its deck. Nevertheless, the full conjecture remains open. Surveys of results on the RC and related problems include [5,12]. Harary and Plantholt [9] defined the reconstruction number of a graph \(G,\) denoted by \(rn(G),\) to be the minimum number of cards which can only belong to the deck of \(G\) and not to the deck of any other graph \(H,~H\ncong G.\) These cards thus uniquely identify \(G.\) Reconstruction numbers are known for only few classes of graphs [2].
An extension of the RC to digraphs is the Digraph Reconstruction Conjecture (DRC), proposed by Harary [7], which asserts that every digraph with at least seven vertices is reconstructible. The DRC was disproved by Stockmeyer [22] by exhibiting several infinite families of counter-examples and this made people doubt the RC itself. To overcome this, Ramachandran [19] introduced degree associated reconstruction for digraphs and proposed a new conjecture in 1981. It was proved [19] that the digraphs in all these counterexamples to the DRC obey the new conjecture, thereby protecting the RC from the threat posed by these digraph counterexamples.
The ordered triple \((a,b,c)\) where \(a,~b\) and \(c\) are respectively the number of unpaired outarcs, unpaired inarcs and symmetric pair of arcs incident with \(v\) in a digraph \(D\) is called the degree triple of \(v.\) The degree associated card or dacard of a graph (digraph) is a pair \((d,C)\) consisting of a card \(C\) and the degree (degree triple) \(d\) of the deleted vertex. The dadeck of a graph (digraph) is the multiset of all its dacards. A graph (digraph) is said to be N-reconstructible if it can be uniquely determined from its dadeck. The new digraph reconstruction conjecture [19] (NDRC) asserts that all digraphs are N-reconstructible. Ramachandran [20,21] then studied the degree associated reconstruction number of graphs and digraphs in 2000. The degree (degree triple) associated reconstruction number of a graph (digraph) \(D\) is the size of the smallest collection of dacards of \(D\) that uniquely determines \(D.\) Articles [6], [15] and [4] are recent papers on the degree associated reconstruction number.
The edge card, edge deck, edge reconstructible graphs and edge reconstruction number are defined similarly with edge deletions instead of vertex deletions. The edge reconstruction conjecture, proposed by Harary [7], states that all graphs with at least 4 edges are edge reconstructible. Edge reconstruction numbers are known for trees [13] and disconnected graphs [3,14]. The degree of an edge \(e,\) denoted by \(d(e),\) is the number of edges adjacent to \(e.\) That is, if \(e=uv\) is an edge, then \(d(e) = d(u)+d(v)-2.\) The ordered pair \((d(e), G-e)\) is called a degree associated edge card or da-ecard of the graph \(G,\) where \(d(e)\) (called the degree of \(e\)) is the number of edges adjacent to \(e\) in \(G.\) The edeck (da-edeck) of a graph \(G\) is its collection of ecards (da-ecards). The degree associated edge reconstruction number of a graph \(G,\) denoted by \(dern(G),\) is the minimum number of da-ecards which can only belong to the da-edeck of \(G\) and not to the da-edeck of any other graph \(H,~H\ncong G.\) These da-ecards thus uniquely identify \(G.\) The \(dern(G)\) has been determined only for few classes of graphs [11,17,16].
By an \(m\)-vertex, we mean a vertex with degree \(m.\) We call a set with size \(m\) by \(m\)-set. The neighbourhood of a vertex \(v\) in a graph \(G\) is written by \(N_G(v)\) (or simply \(N(v)\)). An \(m\)-vertex \(u\) is called an \(m\)-neighbour of \(v\) if \(u\) is a neighbour of \(v;\) otherwise \(u\) is called an \(m\)-nonneighbour of \(v.\) Two vertices \(u\) and \(v\) of a graph \(G\) are said to be bisimilar if there is an automorphism on \(G\) interchanging \(u\) and \(v.\) A graph whose vertices have only one of two possible degrees is called a bidegreed (or biregular) graph. The degree sequence of a bidegreed graph \(G,\) represented by \([d^a, (d+i)^b]\) means that \(G\) contains exactly \(a\) vertices of degree \(d,\) and \(b\) vertices of degree \(d+i,\) where \(i>0.\) A set of vertices \(\{v_1,v_2, \dots, v_k\}\) of a graph \(G\) is said to be a module of \(G\) if \(N_G(v_i)-\{v_1,v_2, \dots, v_k\}= N_G(v_j)-\{v_1,v_2, \dots, v_k\}\) for all \(i, j \in \{1,2,\dots,k \}\).
Myrvold et al. [18] have proved that bidegreed graphs are edge reconstructible (thus degree associated edge reconstructible). Monikandan and Sundar Raj [17] have shown that \(dern(G)=1\) for all regular graphs and few bidegreed graphs \(G\) (namely paths, wheels, bistars, and bidegreed graphs with exactly one vertex of different degree which differs by at least three). On excluding these families of bidegreed graphs, Anu and Monikandan [1] have shown that that \(dern(mK_{1,3})=4\) for \(m>1,\) \(dern(mK_{2,3})=dern(rP_3)=3\) for \(m>0, ~r>1\) and \(dern(G)=1\) or \(2\) for all other bidegreed graphs \(G\) except the \((d,d+1)\)-bidegreed graphs with a \((d+1)\)-vertex adjacent to at least two \(d\)-vertices. In this paper, we prove that \(dern(G)= 1\) or \(2\) for this exceptional bidegreed graphs \(G.\) Thus, \(dern(G)\leq 4\) for all bidegreed graphs \(G.\)
An extension of a da-ecard \((d(e),F-e)\) of a graph \(F\) is a graph obtained from the da-ecard by adding a new edge which joins two nonadjacent vertices whose degree sum is \(d(e)\) and it is denoted by \(H(d(e),F-e)\) (or simply by \(H\)).
For a graph \(F,\) to prove \(dern(F)=k,\) we proceed as follows.
(i) First, find the da-edeck of \(F\).
(ii) Determine next all possible extensions of every da-ecard of \(F.\)
(iii) Finally, show that all extensions other than \(F\) have at most \(k-1\) da-ecards in common with those of \(F,\) and that at least one extension has precisely \(k-1\) da-ecards in common with those of \(F.\)
For sake of clarity, we recall the following three results from [1].
Theorem 2.1. ([1]; Theorem 3) Let \(G\) be a bidegreed graph with degree sequence \([d^a,(d+1)^b].\) Then \(dern(G)=1\) if \(a=1\) or \(b=1.\)
Theorem 2.2. ([1]; Theorem 6) Let \(G\) be a bidegreed graph with degree sequence \([d^a,(d+1)^b],~a,~b\geq2.\) Then \(dern(G)=1\) if and only if
(i) two vertices of minimum degree in \(G\) are adjacent;
(ii) all the \((d+1)\)-vertices in \(G\) are mutually adjacent; or
(iii) any two \(d\)-vertices in a da-ecard of associated degree \(2d-1\) or \(2d\) are bisimilar.
Theorem 2.3. ([1]; Theorem 7) If \(G\) is a bidegreed graph in which all the \((d+1)\)-vertices are mutually nonadjacent, then \(dern(G) = 1,~ 2\) or \(3.\)
Moreover, in Theorem 2.3, \(dern(G)\) is equal to \(3\) only if \(G \cong mK_{2,3}\) or \(G \cong rP_3\) for \(m>0\) and \(r>1.\)
Notation 2.4. For \(i=1,2,…,\) by \(x_i,\) we mean any \(d\)-vertex in \(G;\) by \(y_i\) (or \(z_i\)) super scripted with \(0,1,2,\) or \(3,\) we mean a \((d+1)\)-vertex adjacent to exactly no, one, two or at least three \(d\)-vertices respectively.
Theorem 2.5. If every \((d+1)\)-vertex of a bidegreed graph \(G\) has exactly two \(d\)-neighbours, then \(dern(G)=1~ {\text or}~2.\)
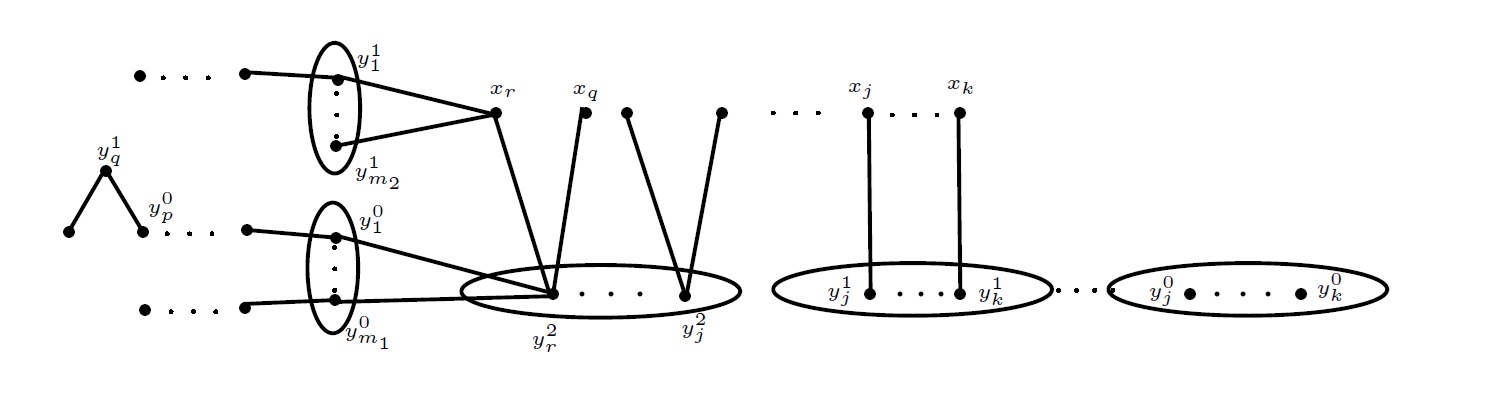
Proof. We assume that \(G\) does not satisfy the hypotheses of Theorems 2.1, 2.2 and 2.3 and hence \(dern(G)\geq 2.\) Let \(y_1^2\) be a \((d+1)\)-vertex and let \(x_1,~x_2\) and \(~y_2^2\) be three neighbours of \(y_1^2.\) Then \(y_1^2\) has exactly \(d-1\) neighbours of degree \(d+1.\) We proceed by two cases depending upon the number of these neighbours that are shared by the vertex \(x_{1}.\)
Case 1. Vertices \(y_1^2\) and \(x_1\) have exactly \(d-1\) common \((d+1)\)-neighbours.
Consider the two da-ecards \((2d-1,G-f)\) and \((2d,G-g),\) where \(f=y_1^2x_2\) and \(g=y_1^2y_2^2.\) By Case 1, vertex \(y_2^2\) is adjacent to \(x_1\) ( Figure 1).
Hence in the da-ecard \((2d,G-g),\) the vertices \(y_1^{2}, x_1\) is a pair of adjacent \(d\)-vertices with other \(d\)-neighbours (namely \(y_2^{2}\) or \(x_2\)) and no three \(d\)-vertices are mutually adjacent.
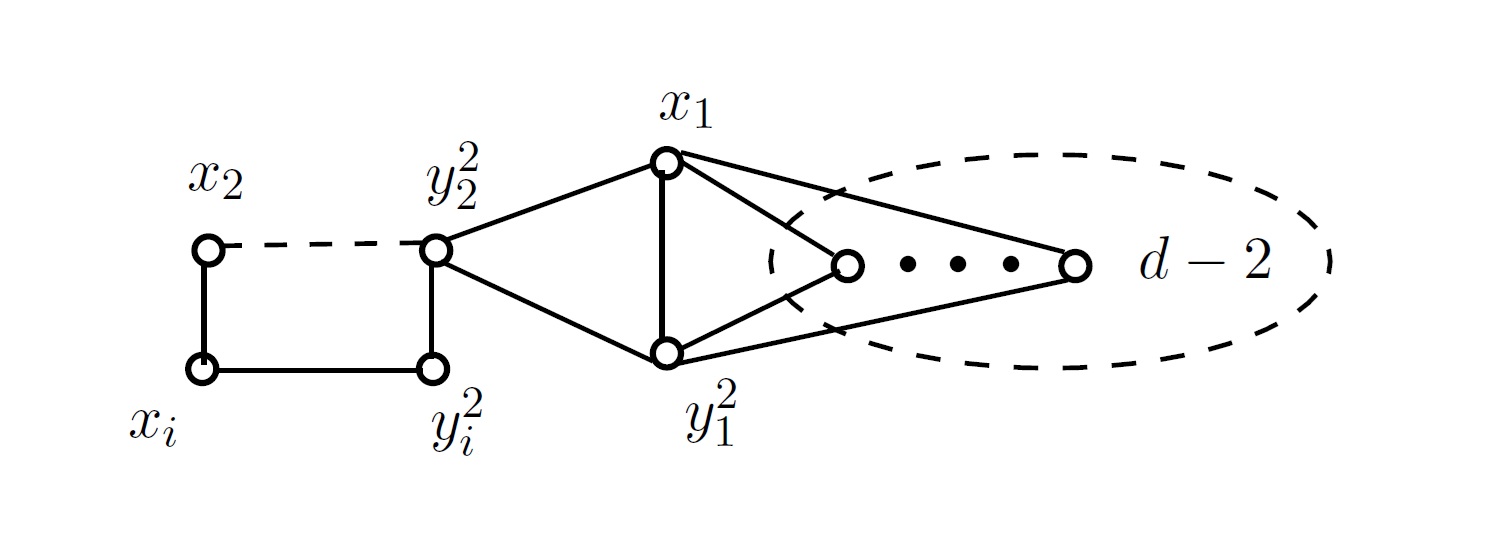
Now consider the extensions of the da-ecard \((2d-1,G-f).\) Note that in the da-ecard \((2d-1,G-f),\) the only adjacent \(d\)-vertices are \(y_1^2, x_1\) and the only \((d-1)\)-vertex is \(x_2.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-f),\) we have to join the \((d-1)\)-vertex \(x_2\) and any one of the \(d\)-vertices, say \(v\) by an edge in \((2d-1,G-f).\) Since \(\{y_1^2, x_1\}\) is a module of \(G-f,\) it follows that \(H \cong G\) when \(v\) is \(y_1^2\) or \(x_1.\) So, we can assume that \(v\) is \(x_i\) for some \(i\neq 1,2\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d, H-e)\) of \(H.\) If \(e\) is \(x_{i}y_j^2\) for some \(j\neq 1,2,\) then, in the da-ecard \((2d, H-e),\) vertices \(y_1^2\) and \(x_1\) would be the only adjacent \(d\)-vertices such that none of them adjacent with other \(d\)-vertices and so \(H-e\ncong G-g.\) Otherwise, \(e\) is \(x_{i}y_2^2\) (if any) or \(y_{2}^{2}y_{i}^2\) for \(i\neq 1.\) Now in the da-ecard \((2d, H-e),\) vertex \(y_2^2\) will become a \(d\)-vertex and the three \(d\)-vertices \(y_2^2,\) \(y_1^2\) and \(x_1\) will become mutually adjacent, which implies \(H-e\ncong G-g.\) Hence every extension \(H(2d, G-f)\) is either isomorphic to \(G\) or any \((2d,H-e)\) da-ecard of \(H\) would contain either two adjacent \(d\)-vertices having no other \(d\)-neighbours or three \(d\)-vertices are mutually adjacent and so \(H-e\) is not isomorphic to \(G-g.\) Hence \(dern(G)\leq2.\)
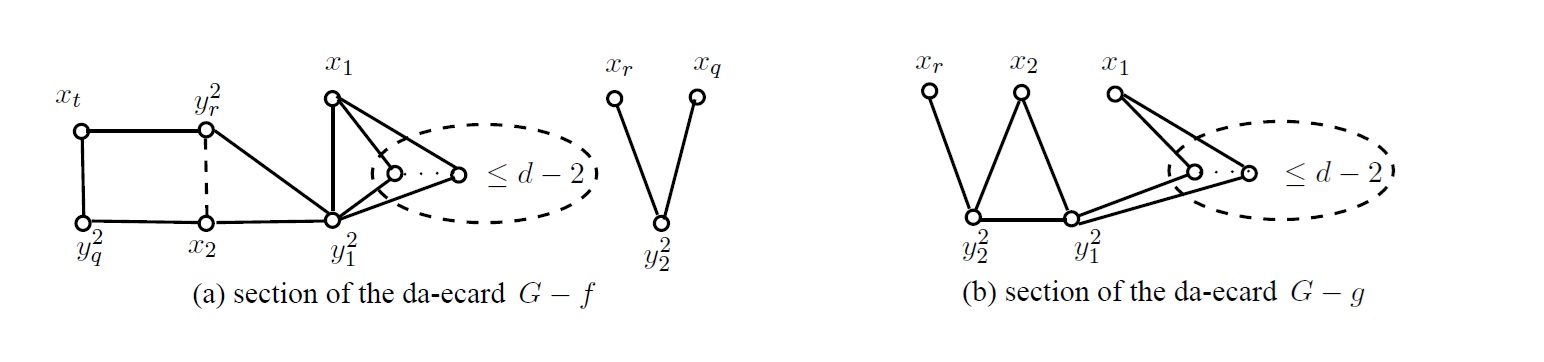
Case 2. Vertices \(x_1\) and \(y_1^2\) have at most \(d-2\) common \((d+1)\)-neighbours.
Let \(y_2^2\) be nonadjacent to \(x_1.\)
Case 2.1. Vertices \(x_2\) and \(y_2^2\) are nonadjacent.
Let \(x_r\) and \(x_q\) be the two \(d\)-neighbours of \(y_2^2.\) Now consider the two da-ecards \((2d, G-f)\) and \((2d-1, G-g),\) where \(f=y_1^2y_2^2\) and \(g=y_1^2x_1.\) In \((2d-1, G-g),\) vertices \(y_1^{2}, x_2\) is a pair of adjacent \(d\)-vertices and \((d-1)\)-vertex nonadjacent to any \(d\)-vertices. In \((2d, G-f),\) exactly six \(d\)-vertices form a \(2K_{1,2}.\) So, to get an extension \(H\) of the da-ecard \((2d, G-f),\) we have to join two \(d\)-vertices, say \(v_1,v_2\) by an edge. If \(\{v_1, v_2\}=\{y_1^2, y_2^2\}\) (Figure 2(a)), then \(H\cong G.\) Otherwise, since the vertices \(v_1\) and \(v_2\) will have degree \(d+1\) in the extension \(H(2d, G-f),\) every da-ecard \((2d-1,H-e)\) of \(H\) has either at least two pairs of adjacent \(d\)-vertices or the unique \((d-1)\)-vertex is adjacent to a \(d\)-vertex, which implies \(H-e\ncong G-g.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d, G-g)\) and hence \(dern( G)\leq 2.\)
Case 2.2. Vertices \(x_2\) and \(y_2^2\) are adjacent.
Let \(x_r\) and \(x_2\) be the two \(d\)-neighbours of \(y_2^2.\) Consider the da-ecards \((2d-1, G-g)\) and \((2d, G-f),\) where \(f=y_1^2y_2^2\) and \(g=y_1^2x_1.\) In \((2d, G-f),\) exactly five \(d\)-vertices together form a path \(P_5\) (say \(w_1,w_2,w_3,w_4,w_5\)) such that each \((d+1)\)-vertex has exactly two \(d\)-neighbours other than \(w_2\) and \(w_4.\) In \((2d-1, G-g),\) the only adjacent \(d\)-vertices are \(y_1^2, x_2\) and the only \((d-1)\)-vertex is \(x_1.\) So, to get an extension \(H\) of the da-ecard \((2d-1, G-g),\) we have to join the \((d-1)\)-vertex \(x_1\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1, G-g)\) by an edge. If \(v\) is \(y_1^2\) (Figure 2(b)), then \(H \cong G.\) Otherwise, \(v\) is \(x_i\) for some \(i\neq 1\) so that it will become a \((d+1)\)-vertex in \(H.\) Now every da-ecard \((2d,H-e)\) of \(H\) has either at least one \((d+1)\)-vertex with exactly one \(d\)-neighbour or no five \(d\)-vertices together form a path \(P_5,\) which implies \(H-e\ncong G-f.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d, G-f)\) and hence \(dern( G)\leq 2.\) ◻
The next result is proved in [1].
Theorem 2.6. ([1]; Theorem 10) If every \((d+1)\)-vertex of a bidegreed graph \(G\) has at most one \(d\)-neighbour, then \(dern(G)=2.\)
In view of Theorems 2.5 and 2.6, we can assume hereafter that \(G\) contains both a \((d+1)\)-vertex (say \(y_r^2\)) adjacent to exactly two \(d\)-vertices (say \(x_r,~x_q\)) and a \((d+1)\)-vertex adjacent to at most one \(d\)-vertex.
Lemma 2.7. Let \(G\) be a bidegreed graph in which vertices of type \(y_r^2,~y_r^0\) exist for some \(r\) and \(y_r^1\) does not exist for any \(r.\) If \(y_r^2\) and a \(d\)-neighbour of it have at most \(d-2\) common \((d+1)\)-neighbours, and \(y_r^2\) is adjacent to some other \(y_q^2,\) then \(dern(G)=1~{\text or}~2.\)
Proof. We assume that \(G\) does not satisfy the hypotheses of Theorems 2.1, 2.2 and 2.3 and hence \(dern(G)\geq2.\) Let \(x_r\) and \(x_q\) be two \(d\)-neighbours of \(y_r^2.\) Let \(y_r^2\) and \(x_r\) have at most \(d-2\) common \((d+1)\)-neighbours.
Case 1. The vertex \(y_q^2\) is nonadjacent to at least one of \(x_r\) and \(x_q.\)
Consider the two da-ecards \((2d,G-y_r^2y_q^2)\) and \((2d,G-y^0z^0)\) (or \((2d,G-y_k^2y^0)\) where \(y^0\in N(y_k^2)\) for some \(k\)). In \(G-y^0z^0\) (or \(G-y_k^2y^0\)), each \(d\)-vertex is nonadjacent to all other \(d\)-vertices ( or there is a unique path of order three lying among \(d\)-vertices such that each \(d\)-vertex not in the path is nonadjacent to the other \(d\)-vertices). In \((2d,G-y_r^2y_q^2),\) there is a unique path of order five lying among \(d\)-vertices (If \(x_r\in N(y_q^2),\) then we obtain the path \(x_qy_r^2x_ry_q^2x_p,\) where \(x_p\in N(y_q^2).\) If \(x_q\in N(y_q^2),\) then we obtain the path \(x_ry_r^2x_qy_q^2x_p,\) where \(x_p\in N(y_q^2)\)) or there are only six \(d\)-vertices together forming \(2K_{1,2}\) (when \(x_r,x_q\notin N(y_q^2)\)). So, to get an extension \(H\) of the da-ecard \((2d,G-y_r^2y_q^2),\) we have to join two \(d\)-vertices by an edge \(e.\) If \(e=y_r^2 y_q^2,\) then \(H \cong G.\) Otherwise, \(e\) is \(y_r^2x_i\) or \(y_q^2x_i\) or \(x_ix_j.\) Now in the da-ecard \((2d, H-e)\) of the resulting extension \(H,\) either no three \(d\)-vertices together form a \(P_3\) or three \(d\)-vertices together form a \(P_3\) but at least one \(d\)-vertex not in the \(P_3\) is adjacent to other \(d\)-vertices. Therefore no da-ecard of \(H\) would be isomorphic to \((2d,G-y^0z^0)\) (or \((2d,G-y_k^2y^0)\)) and hence \(dern(G)\leq 2.\)
Case 2. The vertex \(y_q^2\) is adjacent to both \(x_r\) and \(x_q.\)
Now
if \(y_i^0\) is nonadjacent to any other \(y_j^0\) for all \(i\) and \(j,\) then we consider the two da-ecards \((2d-1,G-y_r^2x_r)\) and \((2d,G-y_i^2y^0)\) for some \(i.\) In the da-ecard \(G-y_i^2y^0,\) exactly three \(d\)-vertices together form a path \(P_3\) (say \(w_1,w_2,w_3\)) but no other \(d\)-vertices are adjacent, there is no \((d+1)\)-vertex adjacent to exactly one \(d\)-vertex other than \(w_2\) and there are \(d\) vertices of degree \(d+1\) adjacent to exactly three \(d\)-vertices other than \(w_2.\) In the da-ecard \((2d-1, G-y_r^2x_r),\) the only adjacent \(d\)-vertices are \(y_r^2, x_q\) and the only \((d-1)\)-vertex is \(x_r.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-y_r^2x_r),\) we have to join the \((d-1)\)-vertex \(x_r\) and any one vertex, say \(v\) among the \(d\)-vertices by an edge in \((2d-1,G-y_r^2x_r).\) If \(v=y_r^2,\) then clearly, \(H \cong G.\) Now, we can assume that \(v\) is \(x_i\) for some \(i\neq q\) so that it will become a \((d+1)\)-vertex in \(H.\) In the da-ecard \((2d, H-e),\) exactly three \(d\)-vertices together form a path \(P_3\) (say \(z_1,z_2,z_3\)) and at least two \(d\)-vertices other than \(z_1,z_2\) and \(z_3\) are adjacent . If \(v\) is \(x_q,\) then, in the da-ecard \((2d, H-e),\) vertex \(x_q\) will become a \((d+1)\)-vertex and at least \(d+1\) vertices of degree \(d+1\) adjacent to exactly three \(d\)-vertices other than \(z_2\) or at least one \((d+1)\)-vertex adjacent to exactly one \(d\)-vertex other than \(z_2.\) Therefore \(H-e\ncong G-y_i^2y^0.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d,G-y_i^2y^0)\) and hence \(dern(G)\leq2.\)
Otherwise, that is \(y^0\) and \(z^0\) are adjacent. If
\(N(x_r)\neq N(x_q),\) then we consider the two da-ecards \((2d,G-y_r^2y_q^2)\) and \((2d,G-y^0z^0).\) In the da-ecard \(G-y^0z^0,\) there are \(2d\) vertices of degree \(d+1\) adjacent to exactly one or three \(d\)-vertices and each \(d\)-vertex is nonadjacent to all other \(d\)-vertices. In the da-ecard \((2d,G-y_r^2y_q^2),\) there is a unique cycle, denoted by \(C_4^d,\) of order four lying among \(d\)-vertices (namely, \(y_r^2x_qy_q^2x_r\)). So, to get an extension \(H\) of the da-ecard \((2d,G-y_r^2y_q^2),\) we have to join two \(d\)-vertices, say \(v_1,v_2\) by an edge \(e.\) If \(\{v_1,v_2\}=\{y_r^2,y_q^2\},\) then clearly, \(H \cong G.\) Otherwise, \(v_1,v_2\) are equal to some \(x_i's,\) where \(i\neq r (\text{or~} q),\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d, H-e)\) of \(H.\) In \((2d, H-e),\) at least two \(d\)-vertices are adjacent. If \(v_1,v_2\) are equal to some \(x_i's,\) where \(i= r,q,\) then, since at least one \((d+1)\)-neighbour of \(x_r\) is adjacent exactly one \(d\)-vertex, the da-ecard \((2d, H-e)\) has at least \(2d+1\) vertices of degree \(d+1\) adjacent to exactly one or three \(d\)-vertices. Therefore no da-ecard of \(H\) would be isomorphic to \((2d,G-y^0z^0)\) and hence \(dern(G)\leq2.\)
Otherwise, that is \(N(x_r)= N(x_q),\) we consider the two da-ecards \((2d-1,G-y_r^2x_r)\) and \((2d,G-y^0z^0).\) In the da-ecard \(G-y^0z^0,\) the set consisting of \(y_r^2\) and all \(d\)-neighbours of \(y_r^2\) is a module and any two \(d\)-vertices are nonadjacent. In the da-ecard \((2d-1,G-y_r^2x_r),\) the only adjacent \(d\)-vertices are \(y_r^2, x_q\) and the only \((d-1)\)-vertex is \(x_r.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-y_r^2x_r),\) we have to join the \((d-1)\)-vertex \(x_r\) and any one vertex, say \(v\) among the \(d\)-vertices by an edge in \((2d-1,G-y_r^2x_r).\) If \(v=y_r^2,\) then clearly, \(H \cong G.\) Now, we can assume that \(v\) is \(x_i\) for some \(i\neq q\) so that it will become a \((d+1)\)-vertex in \(H.\) In the da-ecard \((2d, H-e),\) at least two \(d\)-vertices are adjacent. If \(v\) is \(x_q,\) then, in the da-ecard \((2d, H-e),\) vertex \(x_q\) will become a \((d+1)\)-vertex and it is adjacent to two \(d\)-vertices with distinct neighbourhoods. Therefore \(H-e\ncong G-y^0z^0.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d,G-y^0z^0)\) and hence \(dern(G)\leq2.\) ◻
Lemma 2.8. Let \(G\) be a bidegreed graph in which vertices of type \(y_r^2, ~ y_r^1\) and possibly \(y_r^0\) exist. If \(y_r^2\) and a \(d\)-neighbour of it have at most \(d-2\) common \((d+1)\)-neighbours, and \(y_r^2\) is adjacent to some other \(y_q^2,\) then \(dern(G)=1~{\text or}~2.\)
Proof. We assume that \(G\) does not satisfy the hypotheses of Theorems 2.1, 2.2, 2.3 and Lemma 2.7 and hence \(dern(G)\geq2.\) Let \(x_r\) and \(x_q\) be two \(d\)-neighbours of \(y_r^2.\) Let \(y_r^2\) and \(x_r\) have at most \(d-2\) common \((d+1)\)-neighbours. Let \(y_r^2\) be adjacent to \(y_q^2.\) Suppose \(y_q^2\) is nonadjacent to at least one of \(x_q\) and \(x_r.\) Consider the da-ecards \((2d,G-y_r^2y_q^2)\) and \((2d-1,G-x_sy_s^1),\) where \(y_s^1\) is adjacent to \(x_s.\) Clearly, all the \(d\)-vertices in \(G-x_sy_s^1\) are mutually nonadjacent. Every extension \(H(G-y_r^2y_q^2)\) is either isomorphic to \(G\) or every da-ecard \((2d-1,H-e)\) contains at least two adjacent \(d\)-vertices and so no da-ecard of \(H\) is isomorphic to \((2d-1,G-x_sy_s^1).\)
Suppose that \(y_q^2\) is adjacent to both \(x_q\) and \(x_r.\) We proceed by two cases.
Case 1. Vertex \(y_r^2\) is adjacent to some \(y_s^1.\)
Denote the unique \(d\)-vertex adjacent to \(y_s^1\) by \(x_i.\) If \(x_i=x_r ~(\text{or}~x_q),\) then we choose the two da-ecards \(A_j\) and \(B\) as below. Choose \(A_1=(2d-1,G-y_s^1x_i)\) and \(B=(2d,G-y_r^2y_q^2)\) when \((N(y_r^2)-\{x_i\}\cap N(y_s^1)-\{x_i\})=\phi;\) choose the da-ecards \(A_2=(2d-1,G-y_q^2x_q)\) and \(B\) when \(N(y_r^2)\cap \{y_t^1\}\subseteq N(y_q^2)\) but \(y_t^1\notin N(x_i)\) for some \(t\); choose the da-ecards \(A_3=(2d,G-y_r^2y_s^1)\) and \(B\) when \(N(y_r^2)\cap \{y_t^1\}\subseteq N(y_s^1)\) but \(y_t^1\notin N(x_i)\) for some \(t\); or choose the da-ecards \(A_4=(2d-1,G-y_t^1x_t)\) and \(B\) when \(\{y_t^1\} \subseteq N(y_r^2)\) and \(\{y_t^1\}\notin N(x_r)\cup N(y_s^1)\cup N(y_q^2).\)
The da-ecard \(B\) contains a unique cycle \(C_4^d\) and all the \(d\)-vertices are nonadjacent to every \(d\)-vertex not in \(C_4^d.\) Hence every extension \(H(A_i)\) is either isomorphic to \(G\) or any da-ecard \((2d,H(A_i)-e)\) has one of the following properties.
(i) It has a unique cycle \(C_4^d\) and at least one \(d\)-vertex has a \(d\)-neighbour which is not in \(C_4^d;\)
(ii) the number of copies of \(C_4+e\) containing exactly two \(d\)-vertices in \(H(A_i)-e\) is fewer than that in \(B;\) or
(iii) it has exactly two adjacent \(d\)-vertices.
Hence no da-ecard of \(H(A_i)\) is isomorphic to \(B.\)
Suppose \(\{y_j^0,y_k^0\}\subseteq N(y_r^2).\) If \(y_j^0\) is adjacent to \(y_k^0,\) then choose the two da-ecards \((2d,G-y_r^2y_j^0)\) and \((2d-1,G-y_s^1x_i).\) Now every extension \(H(G-y_r^2y_j^0)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
(i) It has a \((d+1)\)-vertex, say \(y\) adjacent to exactly two \(d\)-vertices and to a \((d+1)\)-vertex having a \(d\)-neighbour not in \(N(y);\) or
(ii) it has a \((d+1)\)-vertex, say \(w\) adjacent to three vertices of degree at most \(d\) and to a \((d+1)\)-vertex having a \(d\)-neighbour not in \(N(w).\)
But the da-ecard \((2d-1,G-y_s^1x_i)\) satisfies none of the above two properties and so it is not a da-ecard of \(H.\)
If \(y_j^0\) is not adjacent to \(y_k^0,\) then consider the two da-ecards \((2d-1,G-y_s^1x_i)\) and \((2d,G-y_r^2y_j^0).\) In \(G-y_s^1x_i,\) there is a unique path, say \(P_3^d\) of order 3 whose vertices are \(d\)-vertices having a common \((d+1)\)-neighbour. Now every extension \(H(G-y_s^1x_i)\) is either isomorphic to \(G\) or any da-ecard \((2d,H-e)\) has one of the following properties:
(i) The number of copies of \(C_4+e\) containing exactly two \(d\)-vertices in \(H(G-y_s^1x_i)\) is fewer than that in \(G-y_s^1x_i;\) or
(ii) there is no \((d+1)\)-vertex as a common neighbour of the \(d\)-vertices in \(P_3^d.\)
Hence no da-ecard of \(H\) is isomorphic to \((2d-1,G-y_s^1x_i).\)
Suppose that \(x_i\neq x_r\) and \(x_i\neq x_q.\) Consider the two da-ecards \((2d-1,G-y_s^1x_i)\) and \((2d,G-y_r^2y_q^2).\) The da-ecard \(G-y_r^2y_q^2\) contains a unique cycle \(C_4^d\) and each \((d+1)\)-vertex is nonadjacent to all the \(d\)-vertices not in \(C_4^d.\) Hence every extension \(H(G-y_s^1x_i)\) is either isomorphic to \(G\) or any \((2d,H-e)\) da-ecard has one of the following properties.
(i) It contains a unique cycle \(C_4^d\) and at least one \((d+1)\)-vertex has a \(d\)-neighbour not in \(C_4^d;\) or
(ii) the number of copies of \(C_4+e\) containing exactly two \(d\)-vertices in \(H(G-y_s^1x_i)-e\) is fewer than that in \(G-y_r^2y_q^2.\)
Hence no da-ecard of \(H(G-y_s^1x_i)\) is isomorphic to \(G-y_r^2y_q^2.\)
Case 2. Vertex \(y_r^2\) is nonadjacent to any \(y_i^1.\)
If some \(y_i^2\) is adjacent to \(x_r\) but not adjacent to \(y_r^2,\) then we consider the two da-ecards \((2d,G-y_r^2y_q^2)\) and \((2d-1,G-y_q^2x_q).\) Clearly the da-ecard \(G-y_q^2x_q\) has a \(K_{1,3}+e\) containing exactly two \(d\)-vertices such that all the neighbours of a \((d+1)\)-vertex in \(K_{1,3}+e\) are nonadjacent to every \(d\)-vertex not in \(K_{1,3}+e.\) Now every extension \(H(G-y_r^2y_q^2)\) is either isomorphic to \(G\) or in any da-ecard \((2d-1,H-e),\) at least one neighbour of a \((d+1)\)-vertex in any \(K_{1,3}+e\) containing exactly two \(d\)-vertices, has a \(d\)-neighbour not lying in it and hence no da-ecard of \(H\) is isomorphic to \((2d-1,G-y_q^2x_q).\) So, we can take that \(N(y_r^2)=\{x_r,x_q,y_1^2,…,y_{r_1}^2,y_1^0,…,y_s^0\}\) and \(N(x_r)=\{y_r^2,y_1^2,…,y_{r_1}^2,z_1^1,…,z_s^1\}.\)
If two adjacent \(z_i^1\)’s (say \(z_1^1,z_2^1\)) are adjacent to \(x_r,\) then we consider the two da-ecards \((2d-1,G-x_rz_1^1)\) and \((2d-1,G-y_r^2x_q).\) In \(G-y_r^2x_q,\) exactly two \(d\)-vertices are adjacent and every uncommon \((d+1)\)-neighbour of these two \(d\)-vertices is nonadjacent to the other \(d\)-vertex. Now every extension \(H(G-x_rz_1^1)\) is either isomorphic to \(G\) or in any da-ecard \((2d-1,H-e),\) two \(d\)-vertices are adjacent and an uncommon \((d+1)\)-neighbour of these two \(d\)-vertices is adjacent to the other \(d\)-vertex and hence no da-ecard of \(H\) is isomorphic to \(G-y_r^2x_q.\) Otherwise, if some \(y_i^0\) (say \(y_s^0\)) is adjacent to both \(y_r^2\) and \(y_q^2,\) then we consider the two da-ecards \((2d,G-y_r^2y_q^2)\) and \((2d-1,G-y_q^2x_r).\) Now every extension \(H(G-y_r^2y_q^2)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties:
(i) It contains an induced subgraph \(K_{1,3}+e\) with exactly two (nonadjacent) \(d\)-vertices having a common \((d+1)\)-neighbour lying outside \(K_{1,3}+e;\) or
(ii) it contains two adjacent \(d\)-vertices, one of which and the unique \((d-1)\)-vertex have a common \((d+1)\)-neighbour.
But the da-ecard \((2d-1,G-y_q^2x_r)\) satisfies none of the above two properties and hence it is not a da-ecard of \(H.\)
Otherwise, if \(z_j^1\in N(y_i^0)\) or \(z_j^1\in N(z_i^1)\) for some \(i\in \{1,2,\cdots,s\}\) and \(j,\) then consider the two da-ecards \((2d-1,G-z_j^1x_j)\) and \((2d-1,G-y_r^2x_r).\) In \(G-y_r^2x_r,\) every \((d+1)\)-neighbour of the two adjacent \(d\)-vertices is not adjacent to any other \(d\)-vertex. Every extension \(H(G-z_j^1x_j)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard of the extension would contain at least one \((d+1)\)-neighbour of the two adjacent \(d\)-vertices is adjacent to the other \(d\)-vertex and hence no da-ecard of \(H\) is isomorphic to \((2d-1,G-y_r^2x_r).\) Otherwise, by proceeding as above, we will get, at some stage, a vertex \(y_p^0\) that is adjacent to \(y_q^1\) or \(y_q^0.\) If the first case happens ( Figure 3), then by proceeding as above, we get \(dern(G)\leq 2.\) If the later case happens, that is, if \(y_p^0\) is adjacent to some \(y_q^0\) but not to any \(y_q^1,\) then consider the two da-ecards \((2d-1,G-z_r^1x_r)\) and \((2d-1,G-y_r^2x_r).\) In \(G-y_r^2x_r,\) exactly two \(d\)-vertices are adjacent. Clearly, every extension \(H(G-z_r^1x_r)\) is either isomorphic to \(G\) or in any da-ecard \((2d-1,H-e),\) all the \(d\)-vertices are mutually nonadjacent and hence no da-ecard of \(H\) is isomorphic to \((2d-1,G-y_r^2x_r).\) ◻
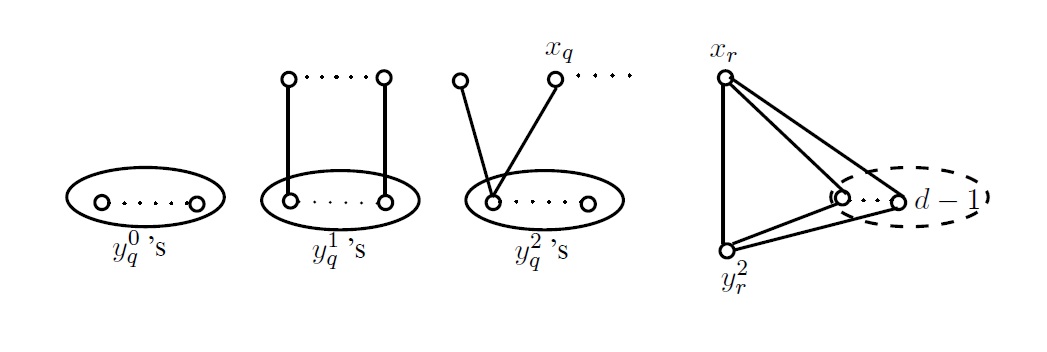
Lemma 2.9. Let \(G\) be a bidegreed graph in which vertices of type \(y_r^2, ~ y_r^1\) and possibly \(y_r^0\) exist. If \(y_r^2\) and a \(d\)-neighbour of it have at most \(d-2\) common \((d+1)\)-neighbours, and \(y_r^2\) is not adjacent to any other vertex of type \(y_i^2,\) then \(dern(G)=1~{\text or}~2.\)
Proof. We assume that \(G\) does not satisfy the hypotheses of Theorems 2.1, 2.2 and 2.3 and hence \(dern(G)\geq2.\) Let \(N(y_r^2)=\{x_{r},x_{q},y_1^0,y_2^0,\cdots,y_{m_1}^0,z_1^1,z_2^1,\cdots,z_{n_1}^1\}\) and
\(N(x_{r})=\{y_1^1,y_2^1,\cdots,y_{m_2}^1,y_1^2,y_2^2,\cdots,y_{n_2}^2\}.\) Suppose that \(m_1\neq m_2\) or \(n_1\neq n_2.\)
If \(n_1\neq n_2\) (or \(n_1=n_2\neq 0\)), then we consider the two da-ecards \((2d-1,G-y_r^2x_q)\) and \((2d-1,G-z_{n_1}^1x_{n_1}).\) Now every extension \(H(G-y_r^2x_q)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties \((\alpha)\) and \((\beta)\).
\((\alpha)\) Every \((d+1)\)-vertex has at most two \(d\)-neighbours; or
\((\beta)\) at most \(m\) vertices of degree \(d+1\) have exactly two \(d\)-neighbours such that
(i) the neighbourhood of each \((d+1)\)-vertex stated in \((\beta)\) can be partitioned into an \(m_1\)-set and an \(n_1\)-set such that every vertex in the \(m_1\)-set has no other \(d\)-neighbours and every vertex in the \(n_1\)-set has exactly one other \(d\)-neighbour, and
(ii) the neighbourhood of one vertex in every pair of \(d\)-vertices stated in \((\beta)\) can be partitioned into an \(m_2\)-set and an \(n_2\)-set, where \(m_1\neq m_2\) and \(n_1\neq n_2\) such that every vertex in the \(m_2\)-set has no other \(d\)-neighbours and every vertex in the \(n_2\)-set has exactly one other \(d\)-neighbour.
But the da-ecard \((2d-1,G-z_{n_1}^1x_{n_1})\) satisfies none of the above properties and hence it would not be a da-ecard of \(H.\) Otherwise, consider the two da-ecards \((2d-1,G-y_r^2x_q)\) and \((2d-1,G-y_{m_2}^{1}x_{r}).\) Now every extension \(H(G-y_r^2x_q)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties \((\alpha)\) and \((\beta)\).
\((\alpha)\) At least one \((d+1)\)-vertex is adjacent to a pair of vertices of degree \(d\) and \(d-1\) respectively, such that \(m_2~(\neq m_1)\) neighbours of this \((d+1)\)-vertex have no other \(d\)-neighbours; or
\((\beta)\) at most \(m\) vertices of degree \(d+1\) in the da-ecard are adjacent to two \(d\)-vertices such that
(i) the neighbourhood of each \((d+1)\)-vertex stated in \((\beta)\) can be partitioned into an \(m_1\)-set and an \(n_1\)-set such that every vertex in the \(m_1\)-set has no other \(d\)-neighbours and every vertex in the \(n_1\)-set has exactly one other \(d\)-neighbour, and
(ii) the neighbourhood of one vertex in each pair of \(d\)-vertices stated in \((\beta)\) can be partitioned into an \(m_2\)-set and an \(n_2\)-set, where \(m_1\neq m_2\) and \(n_1\neq n_2\) such that every vertex in the \(m_2\)-set has no other \(d\)-neighbours and every vertex in the \(n_2\)-set has exactly one other \(d\)-neighbour.
But the da-ecard \((2d-1,G-y_{m_2}^{1}x_{r})\) satisfies none of the above properties and hence it would not be a da-ecard of \(H.\)
Assume now that \(m_1=m_2\) and \(n_1=n_2=0.\) We shall proceed by four cases as below.
Case 1. The set \(\{y_1^0,y_2^0,\dots,y_{m_1}^0\}\) is independent, but \(\{y_1^1,y_2^1,\dots,y_{m_2}^1\}\) is not.
Consider the two da-ecards \((2d-1,G-y_r^2x_{q})\) and \((2d-1,G-y_{m_2}^1x_{r}).\) Now every extension \(H(G-y_r^2x_q)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
\((\alpha)\) At least one \((d+1)\)-vertex is adjacent to a pair of vertices of degree \(d,~d-1\) such that the set of all neighbours of this \((d+1)\)-vertex is not an independent set; or
\((\beta)\) at most \(m\) vertices of degree \(d+1\) are adjacent to two \(d\)-vertices such that the set of all neighbours of one of them is an independent set where as the set of all neighbours of at least one of them is not an independent set.
But the da-ecard \((2d-1,G-y_{m_2}^1x_{r})\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\)
Case 2. The set \(\{y_1^1,y_2^1,\dots,y_{m_2}^1\}\) is an independent set, but \(\{y_1^0,y_2^0,\dots,y_{m_1}^0\}\) is not.
In this case, consider the two da-ecards \((2d-1,G-y_r^2x_{q})\) and \((2d-1,G-y_{m_2}^1x_{r}).\) Now every extension \(H(G-y_r^2x_q)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
\((\alpha)\) At least one \((d+1)\)-vertex is adjacent to a pair of vertices of degree \(d,~d-1\) such that the set of all neighbours of these \((d+1)\)-vertices is an independent set; or
\((\beta)\) at most \(m\) vertices of degree \(d+1\) are adjacent to two \(d\)-vertices such that the set of all neighbours of one of them is not an independent set where as the set of all neighbours of at least one of them is an independent set.
But the da-ecard \((2d-1,G-y_{m_2}^1x_{r})\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\)
Case 3. Both the sets \(\{y_1^0,y_2^0,\dots,y_{m_1}^0\}\) and \(\{y_1^1,y_2^1,\dots,y_{m_2}^1\}\) are independent.
If \(\{y_a^1\}\subseteq N(y_i^0)\) for some \(i\) and \(a\) (respectively \(\{y_b^1\}\subseteq N(y_j^1)\) for some \(j\) and \(b,~y_i^0\) is adjacent to \(y_j^1,\) for some \(i\) and \(j\)), then consider the two da-ecards \((2d-1,G-y_a^1x_a)\) (respectively \((2d-1,G-y_b^1x_b),~(2d-1,G-x_{r}y_j^1)\)) and \((2d-1,G-y_{r}^2x_{q}).\) Now every extension \(H(G-G-y_a^1x_a)\) (respectively \(H(G-y_b^1x_b),~H(G-x_{r}y_j^1\)) is either isomorphic to \(G\) or any da-ecard \((2d-1,H-e)\) has one of the following properties:
\((\alpha)\) At least one \((d+1)\)-neighbour of two adjacent \(d\)-vertices has another \(d\)-neighbour;
\((\beta)\) there is a \((d+1)\)-vertex \(w\) adjacent to two \(d\)-vertices such that at least one neighbour of \(w\) is adjacent to a \(d\)-vertex; or
\((\gamma)\) there is a \((d+1)\)-vertex adjacent to two \(d\)-vertices, say \(w_1,~w_2\) such that at least one neighbour of \(w_1\) or \(w_2\) has exactly one another \(d\)-neighbour.
Hence \(H-e\) is not isomorphic to \((2d-1,G-y_r^2x_q).\) If at least one neighbour of \(y_i^0\) is adjacent to \(y_a^1\) for some \(a;\) then we consider the two da-ecards \((2d-1,G-x_ay_a^1)\) (note that ’\(a\)’ may be equal to \(r\)) and \((2d-1,G-y_r^2x_q).\) Now every extension \(H(G-x_ay_a^1)\) is either isomorphic to \(G\) or any da-ecard \((2d-1,H-e)\) has one of the following properties:
\((\alpha)\) At least one \((d+1)\)-neighbour of one of the adjacent \(d\)-vertices is adjacent to a neighbour of a \(d\)-vertex; or
\((\beta)\) there is a \((d+1)\)-vertex (say \(w\)) adjacent to two \(d\)-vertices such that at least one neighbour of \(w\) is adjacent to a neighbour of a \(d\)-vertex.
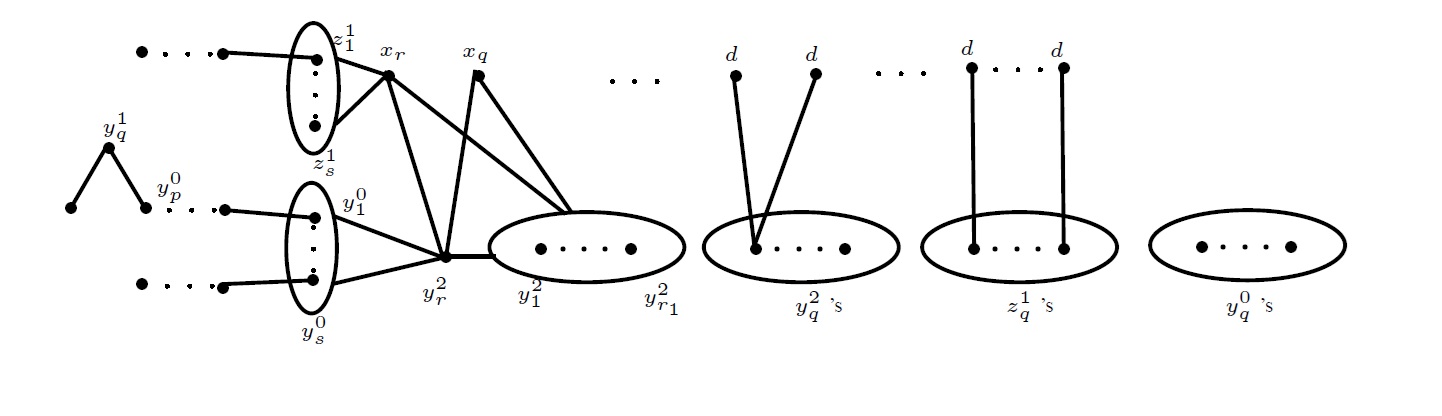
Hence \(H-e\) is not isomorphic to \(G-y_r^2x_q.\) Otherwise, by proceeding as just above, at some stage, we must get a vertex \(y_p^0\) that is adjacent to \(y_q^1\) or \(y_q^0.\) If the former holds (Figure 4), then, by proceeding as above, we get \(dern(G)\leq2.\) If the later holds, that is, if \(y_p^0\) is adjacent to some \(y_q^0\) but not to any \(y_q^1,\) then we consider the two da-ecards \((2d-1,G-y_j^1x_{r})\) and \((2d-1,G-y_r^2x_q),\) where \(1\leq j\leq m_2.\) In \(G-y_r^2x_q,\) there are only two \(d\)-vertices are adjacent. Clearly, every extension \(H(G-y_j^1x_{r})\) is either isomorphic to \(G\) or in any da-ecard \((2d-1,H-e),\) all the \(d\)-vertices are mutually nonadjacent and hence no da-ecard of \(H\) is isomorphic to \((2d-1,G-y_r^2x_q).\)
Case 4. Neither \(\{y_1^0,y_2^0,\dots,y_{m_1}^0\}\) nor \(\{y_1^1,y_2^1,\dots,y_{m_2}^1\}\) is an independent set.
Suppose that \(\{y_a^1\}\subseteq N(y_j^1)\) for some \(j\) and \(a\) (or \(N(y_j^1)=\{y_{r_1}^0,y_{r_2}^0,\dots,y_{r_{d-1}}^0\}\) is an independent set or “\(N(y_j^1)=\{y_{r_1}^0,y_{r_2}^0,\dots,y_{r_{d-1}}^0\}\) is not an independent set and \(y_j^1\) is adjacent to \(y_1^0\)”). The two da-ecards we considered here are \((2d-1,G-x_{r}y_j^1)\) and \((2d-1,G-y_r^2x_{q}).\) Clearly, every extension \(H(G-x_{r}y_j^1)\) is either isomorphic to \(G\) or any da-ecard \((2d-1,H-e)\) has one of the following properties.
\((\alpha)\) Only two \(d\)-vertices are adjacent and a neigbour of exactly one of them is adjacent to a \(d\)-vertex;
\((\beta)\) the set of all neighbours of each \(d\)-vertex is independent; or
\((\gamma)\) at least one \((d+1)\)-vertex (say \(w\)) has two \(d\)-neighbours and each neighbour of \(w\) has a \(d\)-neighbour.
Hence \(H-e\) is not isomorphic to \((2d-1,G-y_r^2x_{q}).\) For other remaining cases, proceeding as in the above two paragraphs, we get \(dern(G)\leq 2.\) This completes Case 4 and our assumption that \(m_1=m_2\) and \(n_1=n_2=0.\)
Finally, we assume that \(m_1=m_2\) and \(n_1=n_2\neq0.\) If \(\{z_j^1\}\subseteq N(z_i^1),~1\leq i,j\leq n_1,\) then consider the two da-ecards \((2d,G-z_i^1z_j^1)\) and \((2d-1,G-y_r^2x_{q}).\) Now every extension \(H(G-z_i^1z_j^1)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties:
\((\alpha)\) There is a \((d+1)\)-vertex adjacent to two \(d\)-vertices such that the set of all neighbours of at least one of them is not an independent set; or
\((\beta)\) at least two \(d\)-vertices are adjacent.
But the da-ecard \((2d-1,G-y_r^2x_{q})\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\) Otherwise, let us assume that \(\{z_j^1\}\not\subseteq N(z_i^1),~1\leq i,j\leq n_1\) for all \(i,~j.\) Suppose \(\{y_k^2\}\subseteq N(z_i^1)\) for some \(k~(y_k^2\neq y_r^2).\) Then we consider the two da-ecards \((2d,G-y_r^2z_i^1)\) and \((2d-1,G-y_{n_2}^2x_{n_2}).\) Now every extension \(H(G-y_r^2z_i^1)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
\((\alpha)\) At least one \((d+1)\)-vertex is adjacent to three vertices of degree at most \(d;\) or
\((\beta)\) there is a unique \(d\)-vertex adjacent to two distinct \(d\)-vertices.
But the da-ecard \((2d-1,G-y_{n_2}^2x_{n_2})\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\) Suppose \(\{y_k^2,y_k^1\}\not\subseteq N(z_i^1)\) for all \(k\) and for some \(i.\) Then consider the two da-ecards \((2d-1,G-z_i^1x_i)\) and \((2d-1,G-y_{r}^2x_{q}).\) Now every extension \(H(G-z_i^1x_i)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
\((\alpha)\) All the neighbours of the unique \((d-1)\)-vertex is nonadjacent to a \(d\)-vertex; or
\((\beta)\) there are only two adjacent \(d\)-vertices and all the neighbours of at least one of them are nonadjacent to all other \(d\)-vertices.
But the da-ecard \((2d-1,G-y_{r}^2x_{q})\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\)
Now, let us take that \(\{y_k^1\}\subseteq N(z_i^1)\) for some \(k.\) Suppose \(\{y_k^1\}\not\subseteq N(y_j^2)\) for all \(k\) and \(1\leq j\leq n_1.\) Consider the two da-ecards \((2d-1,G-y_{r}^2x_{q})\) and \((2d-1,G-z_i^1x_i).\) Every extension \(H(G-y_{r}^2x_{q})\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
\((\alpha)\) There is a \((d+1)\)-vertex (say \(w\)) adjacent to two \(d\)-vertices and a \((d+1)\)-neighbour of \(w\) is nonadjacent to both a \(d\)-vertex and a neighbour of a \(d\)-vertex; or
\((\beta)\) there is a \((d+1)\)-vertex adjacent to three \(d\)-vertices such that all the neighbours of at least one of these \(d\)-vertices are nonadjacent to all other \(d\)-vertices.
But the da-ecard \((2d-1,G-z_i^1x_i)\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\) So, we consider the case that \(\{y_k^1\}\subseteq N(y_j^2)\) for some \(k.\)
If \(\{y_k^2\}\subseteq N(x_i)\) for some \(k\) and \(x_i\in N(z_i^1),\) then we consider the two da-ecards \((2d-1,G-y_{k}^2x_k)\) and \((2d-1,G-y_k^1x_s),\) where \(k\neq i.\) Every extension \(H(G-y_{k}^2x_k)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
\((\alpha)\) There are only two adjacent \(d\)-vertices; or
\((\beta)\) at least one \((d+1)\)-vertex (say \(w\)) has two \(d\)-neighbours such that a \((d+1)\)-neighbour of \(w\) is adjacent to a \((d+1)\)-vertex having two \(d\)-neighbours.
But the da-ecard \((2d-1,G-y_k^1x_s)\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\) Otherwise, consider the two da-ecards \((2d,G-y_{r}^2z_i^1)\) and \((2d-1,G-z_i^1x_i).\) Now every extension \(H(G-y_{r}^2z_i^1)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard has one of the following properties.
\((\alpha)\) At least two \(d\)-vertices are adjacent ; or
\((\beta)\) at least one \((d+1)\)-vertex, say \(w,\) has two \(d\)-neighbours such that a \((d+1)\)-neighbour of \(w\) is adjacent to a \(d\)-vertex in \(N(b_k^2)\) for some \(k.\)
But the da-ecard \((2d-1,G-z_i^1x_i)\) satisfies none of the above two properties and hence it would not be a da-ecard of \(H.\)
Suppose that \(y_k^1\in N(x_i)\) for some \(i,k,\) where \(1\leq i\leq n_1.\) If \(\{z_i^1,y_k^2\}\subseteq N(x_i)\) for some \(i,k\) where \(1\leq i\leq n_1,\) then we consider the da-ecards \((2d-1,G-x_iy_k^2)\) and \((2d-1,G-y_r^2x_q).\) The da-ecard \(G-y_r^2x_q\) contains only one pair of adjacent \(d\)-vertices such that
\((\alpha)\) the neighbour of each of them can be partitioned into an \(m\)-set and an \(n\)-set; and
\((\beta)\) every vertex in the \(m\)-set is adjacent to none of the other \(d\)-vertices and every vertex in the \(n\)-set has exactly one other \(d\)-neighbour (Figure \(6\)).
Hence every extension \(H(G-x_iy_k^2)\) is either isomorphic to \(G\) or any \((2d,H-e)\) da-ecard contains only one pair of adjacent \(d\)-vertices such that
\((\alpha)\) the neighbours of each of them can be partitioned into an \(m_1\)-set and an \(n_1\)-set, where \(m_1>m\) and \(n_1<n;\) or
\((\beta)\) every vertex in the \(m_1\)-set has no other \(d\)-neighbours and every vertex in the \(n_1\)-set has exactly one other \(d\)-neighbour.
Hence no da-ecard of \(H\) would be isomorphic to \((2d-1,G-y_r^2x_q).\) Otherwise, we consider the two da-ecards \((2d,G-y_r^2z_i^1)\) and \((2d-1,G-y_r^2x_q).\) The da-ecard \(G-y_r^2x_q\) contains only one pair of adjacent \(d\)-vertices such that
\((\alpha)\) the neighbour of exactly two (or one) of them can be partitioned into an \(m\)-set and an \(n\)-set;
\((\beta)\) every vertex in the \(m\)-set has no other \(d\)-neighbours and every vertex in the \(n\)-set has exactly one other \(d\)-neighbour (say \(w\)); and
\((\gamma)\) no neighbour of \(w\) has exactly one other \(d\)-neighbour.
Hence every extension \(H(G-x_iy_k^2)\) is either isomorphic to \(G\) or any \((2d-1,H-e)\) da-ecard contains only one pair of adjacent \(d\)-vertices such that
\((\alpha)\) the neighbour of exactly one (or none) of them can be partitioned into an \(m\)-set and an \(n\)-set;
\((\beta)\) every vertex in the \(m\)-set has no other \(d\)-neighbours and every vertex in the \(n\)-set has exactly one other \(d\)-neighbour (say \(w_1\)); or
\((\gamma)\) at least one neighbour of the vertex \(w_1\) has exactly one other \(d\)-neighbour.
Hence no da-ecard of \(H\) would be isomorphic to \((2d-1,G-y_r^2x_q).\) Thus, in all the cases, we have shown that \(dern(G)\leq 2.\) ◻
Theorem 2.10. If every \((d+1)\)-vertex of a bidegreed graph \(G\) has at most two \(d\)-neighbours, then \(dern(G)=1~{\text or}~2.\)
Proof. We assume that \(G\) does not satisfy the hypotheses of Theorems 2.1, 2.2 and 2.3 and hence \(dern(G)\geq2.\) If the vertices \(y_r^2\) and \(x_r\) have at most \(d-2\) common \((d+1)\)-neighbours, then \(dern(G)\leq 2\) by Lemmas 2.7, 2.8 and 2.9 proved. So, we can assume that \(\{y_r^2, x_r\}\) is a module of \(G.\)
Consider the two da-ecards \((2d-1,G-y_r^2x_q)\) and \((2d-1,G-x_rw)\) (or \((2d-1,G-x_py_p^1)\) or \((2d,G-y_p^0y_q^0),\) when \(N(y_r^2)\setminus\{x_r,x_q,w\}=N(x_q)\setminus\{y_r^2,w\}=N(w)\setminus\{y_r^2,x_q,x_r\}~\forall ~w\) hold), where \(w\) is a \((d+1)\)-vertex adjacent to \(x_r\) (Figure 6). In \((2d-1,G-x_rw),\) there are no two adjacent \(d\)-vertices which form a module.
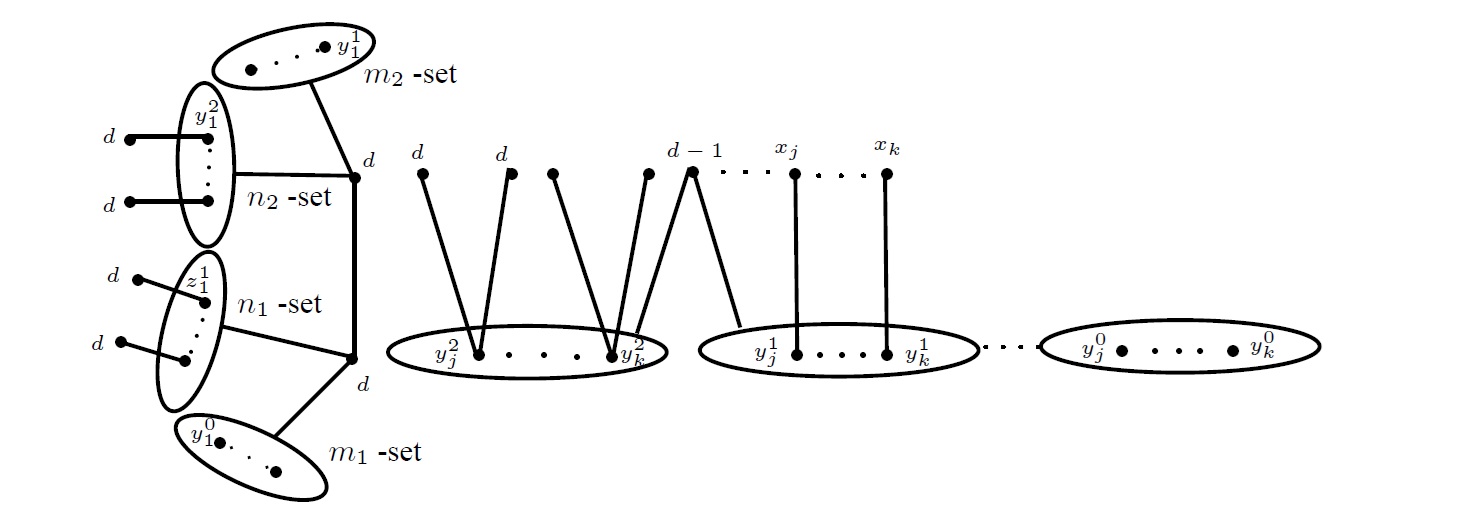
Now consider the extensions of the da-ecard \((2d-1,G-y_r^2x_q).\) Note that in the da-ecard \((2d-1,G-y_r^2x_q),\) the only adjacent \(d\)-vertices are \(y_r^2, x_r\) and the only \((d-1)\)-vertex is \(x_q.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-y_r^2x_q),\) we have to join the \((d-1)\)-vertex \(x_q\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-y_r^2x_q)\) by an edge. Since \(\{y_r^2, x_r\}\) is a module of \(G-y_r^2x_q,\) it follows that \(H \cong G\) when \(v\) is \(y_r^2\) or \(x_r.\) Thus we can assume that \(v\) is \(x_i\) for some \(i\neq r,q\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d-1, H-e)\) (or \((2d, H-e^\prime)\)) of \(H.\) If \(e\) is \(x_{i}y_j^2\) or \(x_iy_j^1,\) (or \(e^\prime\) is \(y_j^sy_k^t,\) where \(s,t=\{0,1,2\}\)) then, in the da-ecard \((2d-1, H-e)\)(or \((2d, H-e^\prime)),~ \{y_r^2,x_r\}\) which form a module and so \(H-e\ncong G-g\) (or \(H-e^\prime\ncong G-g^\prime\)). Therefore no da-ecard of \(H\) would be isomorphic to \((2d-1,G-g)\) (or \((2d,G-g^\prime))\) and hence \(dern(G)\leq2.\) ◻
Theorem 2.11. If only one \((d+1)\)-vertex of a bidegreed graph \(G\) has at least three \(d\)-neighbours, then \(dern(G)=1~{\text or}~2.\)
Proof. We assume that \(G\) does not satisfy the hypotheses of Theorems 2.1, 2.2 and 2.3 and hence \(dern(G)\geq2.\)
Let \(y_1^3\) be adjacent to at least three \(d\)-vertices; let \(x_1,x_2,\dots,x_s\) be \(s~d\)-neighbours of \(y_1^3,\) where \(s\geq3.\)
Case 1. Each \((d+1)\)-neighbour, say \(z\) other than \(y_1^3\) of \(x_1\) has no other \(d\)-neighbours.
Consider the da-ecards \((2d-1,G-f)\) and \((2d-1,G-g),\) where \(f=x_1y_1^3\) and \(g=x_1z.\) In \((2d-1,G-g),\) each \(d\)-vertex is not adjacent to the \((d-1)\)-vertex and all other \(d\)-vertices. In \((2d-1,G-f),\) the only \((d-1)\)-vertex is \(x_1\) and the above \(s~(\geq 3)~d\)-vertices together form \(K_{1,s-1}.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-f),\) we have to join the \((d-1)\)-vertex \(x_1\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-f)\) by an edge. If \(v=y_1^3,\) then clearly, \(H \cong G.\) Otherwise, \(v=x_j\) for some \(j\neq 1\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d-1, H-e)\) of \(H.\) If \(e\) is \(x_{i}y_1^3\) for some \(i\neq 1,j\) then, in the da-ecard \((2d-1, H-e),\) at least one \(d\)-vertex has a \((d-1)\)-neighbour and thus \(H-e\ncong G-g.\) Otherwise, \(e\) is \(x_{i}y_{j}\) (if any). Now in the da-ecard \((2d-1, H-e),\) \(k~(<s)~d\)-vertices together form \(K_{1,k-1}\) or at least one \(d\)-vertex has \((d-1)\)-neighbour. Therefore \(H-e\ncong G-g.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d-1,G-g)\) and hence \(dern(G)\leq2.\)
Case 2. There is a \((d+1)\)-neighbour, say \(z\) of \(x_1\) other than \(y_1^3,\) having a \(d\)-neighbour other than \(x_1.\)
Case 2.1. \(s \geq 4.\)
For this case, we use the da-ecards \((2d-1,G-f)\) and \((2d-1,G-g),\) where \(f=x_1y_1^3\) and \(g=x_1z.\) In \((2d-1,G-g),\) each \(d\)-vertex is nonadjacent to the \((d-1)\)-vertex and to only one pair of adjacent \(d\)-vertices. In \((2d-1,G-f),\) the only \((d-1)\)-vertex is \(x_1\) and give the \(s+2~(s\geq4)~d\)-vertices which together form \(K_{1,s-1}\cup K_2.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-f),\) we have to join the \((d-1)\)-vertex \(x_1\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-f)\) by an edge. If \(v=y_1^3,\) then clearly, \(H \cong G.\) Otherwise, \(v\) is equal to \(x_i\) for some \(i\neq 1\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d-1, H-e)\) of \(H.\) If \(e\) is \(x_{i}y_1^3\) for some \(i\neq 1,\) then, in the da-ecard \((2d-1, H-e),\) at least one \(d\)-vertex has a \((d-1)\)-neighbour and so \(H-e\ncong G-g.\) Otherwise, \(e\) is \(x_{i}y_{j}\) (if any). Now in the da-ecard \((2d-1, H-e),\) \(k+2~(<s+2~(s\geq4))~d\)-vertices together form \(K_{1,k-1}\cup K_2\) or at least one \(d\)-vertex has a \((d-1)\)-neighbour. Hence \(H-e\ncong G-g.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d-1,G-g)\) and hence \(dern(G)\leq2.\)
Case 2.2. \(s=3.\)
Case 2.2.1. Vertex \(y_1^3\) is adjacent to a neighbour of \(x_i\) for some \(i,~1\leq i\leq 3.\)
Now if \(|N(x_1)\cap N(x_2)|=d,\) then we consider the two da-ecards \((2d-1,G-f)\) and \((2d,G-g),\) where \(f=y_1^3x_3\) and \(g=y_1^3z.\) In \(G-g,\) exactly one \(d\)-vertex (say \(w_1\)) has three \(d\)-neighbours of which exactly two neighbours (say \(a_1\) and \(a_2\)) have a common \(d\)-neighbour (other than \(w_1\)) and \(|N(w_1)\cap N(a_1)\cap N(a_2)|=m\) (say). Hence every extension \(H(G-f)\) is either isomorphic to \(G\) or in any \((2d,H-e)\) da-ecard,
(i) each \(d\)-vertex has at most two \(d\)-neighbours; or
(ii) a \(d\)-vertex (say \(w\)) has three \(d\)-neighbours of which exactly two neighbours (say \(b_1\) and \(b_2\)) have a common \(d\)-neighbour such that \(|N(w)\cap N(b_1)\cap N(b_2)|\geq m+1.\)
Hence no da-ecard of \(H\) is isomorphic to \(G-g.\) Otherwise, that is, \(|N(x_1)\cap N(x_2)|\leq d-1.\) Now if a \((d+1)\)-vertex \(z\) is nonadjacent to \(x_i~(i=2,3)\) and it is adjacent to \(y_1^3,\) then choose the two da-ecards \((2d,G-f)\) and \((2d-1,G-g),\) where \(f=y_1^3z\) and \(g=x_1z.\) Clearly every extension \(H(G-f)\) is either isomorphic to \(G\) or in any da-ecard \((2d-1,H-e),\) the neighbour of the unique \((d-1)\)-vertex has three \(d\)-neighbours of which at least two are adjacent to a \(d\)-vertex. Hence \(H-e\) is not isomorphic to \(G-g\) and thus \(dern(G)\leq 2.\) Otherwise, choose the two da-ecards \((2d-1,G-f)\) and \((2d,G-g)\) where \(f=y_1^3x_3\) and \(g=y_1^3z.\) In \(G-g,\) exactly one \(d\)-vertex (say \(w_1\)) is adjacent to three \(d\)-neighbours of which exactly two (say \(a_1\) and \(a_2\)) have a common \(d\)-neighbour, \(|N(a_1)\cap N(a_2)|=m_1\) (say) and \(|N(w_1)\cap N(a_1)\cap N(a_2)|=m_2\) (say), where \(m_1>m_2.\) Clearly, every extension \(H(G-f)\) is either isomorphic to \(G\) or in any da-ecard \((2d,H-e),\) each \(d\)-vertex has at most two \(d\)-neighbours or the unique \(d\)-vertex (say \(w\)) has three \(d\)-neighbours of which exactly two (say \(b_1\) and \(b_2\)) have a common \(d\)-neighbour such that \(|N(w)\cap N(b_1)\cap N(b_2)|\geq m_2+1\) or \(|N(b_1)\cap N(b_2)|\leq m_1-1.\) Hence no da-ecard of \(H\) is isomorphic to \(G-g\) and thus \(dern(G)\leq 2.\)
Case 2.2.2. Vertex \(y_1^3\) is not adjacent to any neighbour of \(x_i\) for \(1\leq i\leq 3.\)
Let the neighbours of \(y_1^3\) be \(w_1,w_2,…,w_{d-2}.\) Then choose two da-ecards as below.
Choose \(A_1=(2d,G-f)\) and \(B_1=(2d-1,G-g),\) where \(f=y_1^3w_1\) and \(g=x_1z,\) when \(w_1\) has two \(d\)-neighbours; choose \(A_2=(2d-1,G-f)\) and \(B_2=(2d-1,G-g)\) when \(w_1\) has exactly one \(d\)-neighbour (say \(a_1\)), where \(f=x_1y_1^3\) and \(g=w_1a_1\); choose \(A_2\) and \(B_3=(2d,G-g)\) when \(w_1\) is adjacent to a vertex \(w_2,\) where \(g=w_1w_2;\) choose \(A_2\) and \(B_4=(2d,G-g)\) when no two \(w_i\)’s are adjacent and a neighbour (say \(w\)) of \(w_1\) has no \(d\)-neighbours, where \(g=ww_1\); choose \(A_2\) and \(B_5=(2d-1,G-g)\) when no two \(w_i\)’s are adjacent and a neighbour (say \(w\)) of \(w_1\) has exactly one \(d\)-neighbour (say \(a_2\)), where \(g=wa_2\) ; or choose finally \(A_2\) and \(B_6=(2d,G-g),\) where \(g=y_1^3w_1,\) when no two \(w_i\)’s are adjacent and a neighbour of \(w_1\) is adjacent to two \(d\)-vertices.
Among the \(d\)-vertices in \(B_1,\) exactly one pair of vertices is adjacent. Hence every extension \(H(A_1)\) is either isomorphic to \(G\) or in any da-ecard \((2d-1,H(A_1)-e),\) at least two pairs of \(d\)-vertices are adjacent or at least one \(d\)-vertex has at least two \(d\)-neighbours. In \(B_i~(i\geq2),\) all the \(d\)-vertices are mutually nonadjacent. Hence every extension \(H(A_2)\) is either isomorphic to \(G\) or in any da-ecard \((k, H(A_2)-e),\) where \(k=2d~\text{or}~2d-1,\) at least two \(d\)-vertices are adjacent and hence no da-ecard of \(H(A_i)~(i=1,~2)\) is isomorphic to \(B_i.\) Thus, in all the cases, we have shown that \(G\) has at most one da-ecard in common with \(H,\) where \(H\ncong G\) and hence \(dern(G)\leq 2.\) ◻
Theorem 2.12. If at least two \((d+1)\)-vertices of a bidegreed graph \(G\) has at least three \(d\)-neighbours, then \(dern(G)=1~{\text or}~2.\)
Proof. We assume that \(G\) does not satisfy the hypotheses of Theorems 2.1, 2.2 and 2.3 and hence \(dern(G)\geq2\) and at least two \((d+1)\)-vertices in \(G\) are adjacent. Since \(G\) contains at least two \(y_i^3\)s, we proceed by two cases depending on their adjacencies.
Case \(1.\) At least two \(y_i^{m_1}\)’s are adjacent, where \(m_1~(\geq3)\) is minimum.
Let \(A\) be the collection of all \(y_i^3\)’s in \(G.\) Then \(|A|\geq2.\) Let \(B\) be the set of all vertices in \(A\) that are adjacent to the minimum number of (or \(m_1\)) \(d\)-vertices. Let \(C\) be the set of all vertices in \(B\) that are adjacent to a vertex in \(B.\) Then the set \(C\) is non-empty by Case 1. Choose a vertex, say \(y_p^{m_1}\) in \(C\) that is adjacent to the minimum number (say \(m_2\)) of \((d+1)\)-vertices in \(B.\)
Consider the two da-ecards \((2d-1,G-x_py_p^{m_1})\) and \((2d,G-y_p^{m_1}y_q^{m_1}),\) where \(\{x_p,y_q^{m_1}\}\in N(y_p^{m_1}).\) In \(G-y_p^{m_1}y_q^{m_1},\) one of the two nonadjacent \(d\)-vertices is adjacent to \(m_1\) (respectively \(m_2-1\)) vertices of degree \(d\) (respectively \(d+1\)) and each of these \((d+1)\)-vertices has at least \({m_1}+1~d\)-neighbours. In \((2d-1,G-x_py_p^{m_1}),\) the only \((d-1)\)-vertex is \(x_p\) and the \(m_1~(\geq 3)~d\)-vertices together form \(K_{1,m_1-1}\) such that \(y_p^{m_1}\) has \(m_2~(d+1)\)-neighbours in \(B.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-x_py_p^{m_1}),\) we have to join the \((d-1)\)-vertex \(x_p\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-x_py_p^{m_1})\) by an edge. If \(v=y_p^{m_1},\) then clearly, \(H \cong G.\) Otherwise, \(v\) is equal to \(x_i\) for some \(i\neq p\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d, H-e)\) of \(H.\) If \(e\) is \(w_iw_j,\) where \(w_i\) or \(w_j\in N(y_p^{m_1})\) then, in the da-ecard \((2d, H-e),\) one of the two nonadjacent \(d\)-vertices is adjacent to at least \(m_1\) (respectively at most \(m_2-1\)) vertices of degree \(d\) (respectively \(d+1\)) and each of these \((d+1)\)-vertex has at least \({m_1}+1~d\)-neighbours and thus \(H-e\ncong G-y_p^{m_1}y_q^{m_1}.\) Otherwise, \(e\) is \(w_iw_j,\) where \(w_i,~w_j\notin N(y_p^{m_1}).\) Now, in the da-ecard \((2d-1, H-e),\) one of the two nonadjacent \(d\)-vertices is adjacent to \(m_1-1\) (respectively \(m_2\)) vertices of degree \(d\) (respectively \(d+1\)) and each of these \((d+1)\)-vertices has at least \({m_1}+1~d\)-neighbours and thus \(H-e\ncong G-y_p^{m_1}y_q^{m_1}.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d,G-y_p^{m_1}y_q^{m_1})\) and hence \(dern(G)\leq2.\)
Case 2. Any two \(y_i^{m_1}\)’s are nonadjacent, where \(m_1~(\geq3)\) is minimum.
Let \(n_0,n_1,n_2,\cdots,n_s\) be the number of \((d+1)\)-vertices adjacent to exactly \(0,1,2,\cdots,s\) vertices of degree \(d,\) respectively. Let \(y_p^i\) and \(w\) be adjacent, respectively, to exactly \(i\) and \(j\) vertices of degree \(d.\)
Case 2.1. \(|i-j|\geq2,~0\leq j<i\leq s,~i\geq3.\)
Case 2.1.1. \(j\geq1.\)
Consider the two da-ecards \((2d-1,G-x_py_p^i)\) and \((2d-1,G-x_rw),\) where \(x_p\in N(y_p^i)\) and \(x_r\in N(w).\) In \(G-x_rw,\) there is a unique \(d\)-vertex having exactly \(j-1~d\)-neighbours and each \(d\)-vertex is not adjacent to the \((d-1)\)-vertex. In \((2d-1,G-x_py_p^i),\) the only \((d-1)\)-vertex is \(x_p\) and the above \(i~(\geq 3)~d\)-vertices together form \(K_{1,i-1}.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-x_py_p^i),\) we have to join the \((d-1)\)-vertex \(x_p\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-x_py_p^i)\) by an edge. If \(v=y_p^i,\) then clearly, \(H \cong G.\) Otherwise, \(v\) is equal to \(x_k\) for some \(k\neq p\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d-1, H-e)\) of \(H.\) If \(e\) is \(x_{k}z,\) then the da-ecard \((2d-1, H-e)\) has a unique \(d\)-vertex adjacent to at least \(j\) \(d\)-vertices or at least one \(d\)-vertex is adjacent to the \((d-1)\)-vertex. Hence \(H-e\ncong G-x_rw\) and no da-ecard of \(H\) would be isomorphic to \((2d-1,G-x_rw).\)
Case 2.1.2. \(j=0.\)
If at least two \(y_k^0\)’s are adjacent, then choose the two da-ecards \((2d-1,G-x_py_p^i)\) and \((2d,G-y_p^0y_q^0),\) where \(x_p\in N(y_p^i)\) and \(y_q^0\in N(y_p^0).\) In \(G-y_p^0y_q^0,\) all the \(d\)-vertices are mutually nonadjacent. In \((2d-1,G-x_py_p^i),~i~(\geq 3)~d\)-vertices together form \(K_{1,i-1}.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-x_py_p^i),\) we have to join the \((d-1)\)-vertex \(x_p\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-x_py_p^i)\) by an edge. If \(v=y_p^i,\) then clearly, \(H \cong G.\) Otherwise, \(v\) is equal to \(x_k\) for some \(k\neq p\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d, H-e)\) of \(H.\) If \(e\) is \(w_iw_j,\) then, in the da-ecard \((2d, H-e),~i~(\geq 2)~d\)-vertices together form \(K_{1,i-1}\) and thus \(H-e\ncong G-y_p^0y_q^0.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d,G-y_p^0y_q^0).\) Otherwise, choose the two da-ecards \((2d-1,G-x_py_p^i)\) and \((2d,G-y_p^0y_p^i),\) where \(\{x_p,y_p^0\}\subseteq N(y_p^i).\) In \(G-y_p^0y_p^i,\) the unique \(d\)-vertex has \(i~d\)-neighbours. In \((2d-1,G-x_py_p^i),~i~(\geq 3)~d\)-vertices together form \(K_{1,i-1}.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-x_py_p^i),\) we have to join the \((d-1)\)-vertex \(x_p\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-x_py_p^i)\) by an edge. If \(v=y_p^i,\) then clearly, \(H \cong G.\) Otherwise, \(v\) is equal to \(x_k\) for some \(k\neq p\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d, H-e)\) of \(H.\) If \(e\) is \(w_iw_j,\) then, in the da-ecard \((2d, H-e),\) the unique \(d\)-vertex has at most \(i-1~d\)-neighbours or at least two \(d\)-vertices adjacent to other \(d\)-vertices and thus \(H-e\ncong G-y_p^0y_p^i.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d,G-y_p^0y_p^i)\) and hence \(dern(G)\leq2.\)
Case 2.2. \(|i-j|\leq1.\)
The proof follows by Case 1 when \(i=j\). For \(i\neq j,\) consider the da-ecards \((2d-1,G-x_py_p^i)\) and \((2d,G-y_p^iy_p^{i-1}),\) where \(\{x_p,y_p^{i-1}\}\subseteq N(y_p^i).\) In \(G-y_p^iy_p^{i-1},\) exactly two nonadjacent \(d\)-vertices such that one of them adjacent to \(i~d\)-vertices and the other adjacent to \(i-1~d\)-vertices. In \((2d-1,G-x_py_p^i),\) the only \((d-1)\)-vertex is \(x_p\) and the above \(i~(\geq 3)~d\)-vertices together form \(K_{1,i-1}.\) So, to get an extension \(H\) of the da-ecard \((2d-1,G-x_py_p^i),\) we have to join the \((d-1)\)-vertex \(x_p\) and any one vertex, say \(v\) among the \(d\)-vertices in \((2d-1,G-x_py_p^i)\) by an edge. If \(v=y_p^i,\) then clearly, \(H \cong G.\) Otherwise, \(v\) is equal to \(x_k\) for some \(k\neq p\) so that it will become a \((d+1)\)-vertex in \(H.\) Now consider all possible da-ecards \((2d, H-e)\) of \(H.\) If \(e\) is \(w_iw_j,\) then, in the da-ecard \((2d, H-e),\) at least three nonadjacent \(d\)-vertices adjacent to other \(d\)-vertices and thus \(H-e\ncong G-y_p^iy_p^{i-1}.\) Thus no da-ecard of \(H\) would be isomorphic to \((2d,G-y_p^iy_p^{i-1})\) and hence \(dern(G)\leq2.\) ◻
Myrvold et al. [18] proved that bidegreed graphs are edge reconstructible. But the edge reconstruction number of bidegreed graphs, except for a few classes, is not known. This paper together with [1] have completely determined the degree associated edge reconstruction number of all bidegreed graphs and it is at most four. The degree associated edge reconstruction parameter might be a strong tool for providing evidence to support or reject the Edge Reconstruction Conjecture that remains open.
We are thankful to the anonymous referee for giving very valuable comments on earlier versions of this manuscript. Monikandan’s research is supported by the National Board for Higher Mathematics(NBHM), Department of Atomic Energy, Mumbai through a Major Research Project, Grant No. 02011/14/2022/NBHM(R.P)/\(\text{R}\&\text{D}\)-II/10491.